Матрицы и камеры
Производителей цифровых камер больше, чем тех кто «умеет» делать матрицы. Схем используемых объективов не много. Но споры о том, чьи фотографии лучше не прекращаются. Алгоритмы преобразования сигнала с матрицы «в файл», дизайн и пользовательские функции — то, над чем собственно и могут потрудиться «фирменные» конструкторы.
И все же интересно — много ли зависит от матрицы и могут ли камеры с близкими по характеристикам CCD/CMOS (или даже идентичными) сильно отличаться по фотографическим возможностям и изображению.
Для сравнения были взяты экземпляры распространенных и очень удачных цифровых камер «полупрофессионального» уровня. Все они уже были испытаны ранее и описаны. Технические характеристики и описания: Canon Power Shot G2, Olympus C-5050ZOOM, Casio QV4000 и здесь, Casio QV5700, Nikon Coolpix 5000. Данные о матрицах взяты из этих же материалов, а так же статей о матрицах и итогах года. В прочем SONY и Panasonic не держат секретов об уже выпущенных светочувствительных чипах и найти их описание можно через любую поисковую систему в сети. Труднее установить, что же конкретно установлено в цифровой фотоаппарат.
Труднее установить, что же конкретно установлено в цифровой фотоаппарат.
Отобранные для сравнения аппараты интересны тем, что два из них практически идентичны по конструкции, но имеют матрицы разных производителей и разрешения (Casio), Canon G2 и Casio QV4000 собраны на одинаковых матрицах и объективах, но различны по конструкции и используемым алгоритмам «оцифровки», 5-ти мегапиксельные аппараты собраны на матрицах разных производителей и размеров. Так что есть, что сравнить.
То, что дизайнеры могут по разному использовать ресурсы матриц хорошо видно на примере Canon G2 и Casio QV4000. При одной и той же матрице и объективе, аппараты отличаются максимальным форматом кадра, диапазоном возможных светочувствительностей (у Casio вообще единственное базовое значение ISO) и наличием RAW (у Casio формально RAW нет). Возможно, что такая «искусственная скромность» Casio результат «рыночного соглашения». И это вполне вероятно — ведь множество функций Casio QV4000 скрыты от «рядового пользователя» (смотри здесь) но все же существуют. Прямой конкурент Casio QV5700 с 1/1,8″ матрицей Panasonic — Olympus C-5050 с такой же по размеру и разрешению матрицей от Sony. В Nikon Coolpix 5000 установлена 5 мегапиксельная и в 2/3″ — большая матрица с наибольшим размером отдельного чувствительного элемента — 3,4 микрона. При таком «большом» элементе и матрице максимальная диафрагма в F/8 и то только для широкого угла выглядит скромной в сравнении с F/10 у Olympus с его меньшей матрицей.
Прямой конкурент Casio QV5700 с 1/1,8″ матрицей Panasonic — Olympus C-5050 с такой же по размеру и разрешению матрицей от Sony. В Nikon Coolpix 5000 установлена 5 мегапиксельная и в 2/3″ — большая матрица с наибольшим размером отдельного чувствительного элемента — 3,4 микрона. При таком «большом» элементе и матрице максимальная диафрагма в F/8 и то только для широкого угла выглядит скромной в сравнении с F/10 у Olympus с его меньшей матрицей.
| камера | Canon PowerShot G2 | Olympus С-5050 Zoom | Casio QV4000 | Casio QV5700 | Nikon 5000 |
| матрица | Sony ICX406AQ | Sony | Sony ICX406AQ | Panasonic MN39594PH-L | Sony ICX282 |
| матрица, размер | 1/1,8″ | 1/1,8″ | 1/1,8″ | 1/1,8″ | 2/3″ |
| матрица, эффективных элементов млн | 3,9 | 4,92 | 3,98 | 4,92 | 4,92 |
| Размер элемента мкм | 3,12×3,12 | 2,775×2,775 | 3,12×3,12 | 2,7×2,7 | 3,4×3,4 |
| чувствительность | 50, 100, 200, 400 | 100, 200, 400 | 64 (100) | 50, 100, 200, 400, 800 | 100, 200, 400, 800 |
| кадр | 2272×1704 | 2560×1920 | 2240×1680 | 2560×1920 | 2560×1920 |
| диафрагма | F/2,0 — F/2,5 -F/8 | F/1,8 — F/10 | F/2,0 — F/2,5 -F/8 | F/2,0 — F/2,5 -F/8 | W F/2,8 — F/8 |
Одной из ключевых характеристик цифрового фотоаппарата является его «шумность». Она и была использована для сравнения камер. Про методики определения и оценки шум можно посмотреть здесь и здесь. «Мерой шумности для цифровой фотографии можно считать стандартное отклонение — среднеквадратичное отклонение от среднего, которое выводит Photoshop для всей картинки или выделенной ее области в меню «Гистограмма» (можно смотреть значение среднего и отклонения для яркости L или любого из цветов выбранного цветового пространства RGB, HSB, LAB)».
Она и была использована для сравнения камер. Про методики определения и оценки шум можно посмотреть здесь и здесь. «Мерой шумности для цифровой фотографии можно считать стандартное отклонение — среднеквадратичное отклонение от среднего, которое выводит Photoshop для всей картинки или выделенной ее области в меню «Гистограмма» (можно смотреть значение среднего и отклонения для яркости L или любого из цветов выбранного цветового пространства RGB, HSB, LAB)».
При испытаниях на световой столик укладывалась молочная пленка, запечатанная черными чернилами различной плотности в четырех отдельных зонах. Камера устанавливалась на штатив и производилась съемка с максимальной и минимальной возможной для камеры чувствительностью. Для сглаживания неоднородностей тестового объекта объектив камеры расфокусировался, а диафрагма устанавливалась максимально открытой. Баланс белого устанавливался вручную, экспозиция по экспонометру и с вилкой ±1 ступень выдержки. Съемка производилась в TIFF или RAW. Из снимка вырезались 4 квадратика различной оптической плотности размером 150×150 пикс. Таким образом для каждого фотоаппарата было получено по набору однородных квадратиков для максимальной и минимальной чувствительности. С помощью Photoshop можно определить для каждого из квадратиков значение яркости L и стандартного отклонения яркости dL. Далее не составит труда построить зависимость шума от яркости L. Величиной, характеризующей шум традиционно считается 20хLg(dL/L). Исходные данные в Excel можно посмотреть здесь. Зависимость шума от яркости для каждой камеры представлена в фильме Shockwave Flash:Для удобства сравнения можно «включить» только необходимые камеры и величины светочувствительности.
Из снимка вырезались 4 квадратика различной оптической плотности размером 150×150 пикс. Таким образом для каждого фотоаппарата было получено по набору однородных квадратиков для максимальной и минимальной чувствительности. С помощью Photoshop можно определить для каждого из квадратиков значение яркости L и стандартного отклонения яркости dL. Далее не составит труда построить зависимость шума от яркости L. Величиной, характеризующей шум традиционно считается 20хLg(dL/L). Исходные данные в Excel можно посмотреть здесь. Зависимость шума от яркости для каждой камеры представлена в фильме Shockwave Flash:Для удобства сравнения можно «включить» только необходимые камеры и величины светочувствительности.
Лучший результат при минимальной чувствительности у Nikon 5000. И это не удивительно — его чувствительный элемент наибольший, а система фильтров C-Y-G-M теоретически использует свет более эффективно, чем G-R-G-B. Так же вполне логично и то, что Canon G2 и Casio QV4000 шумят почти одинаково.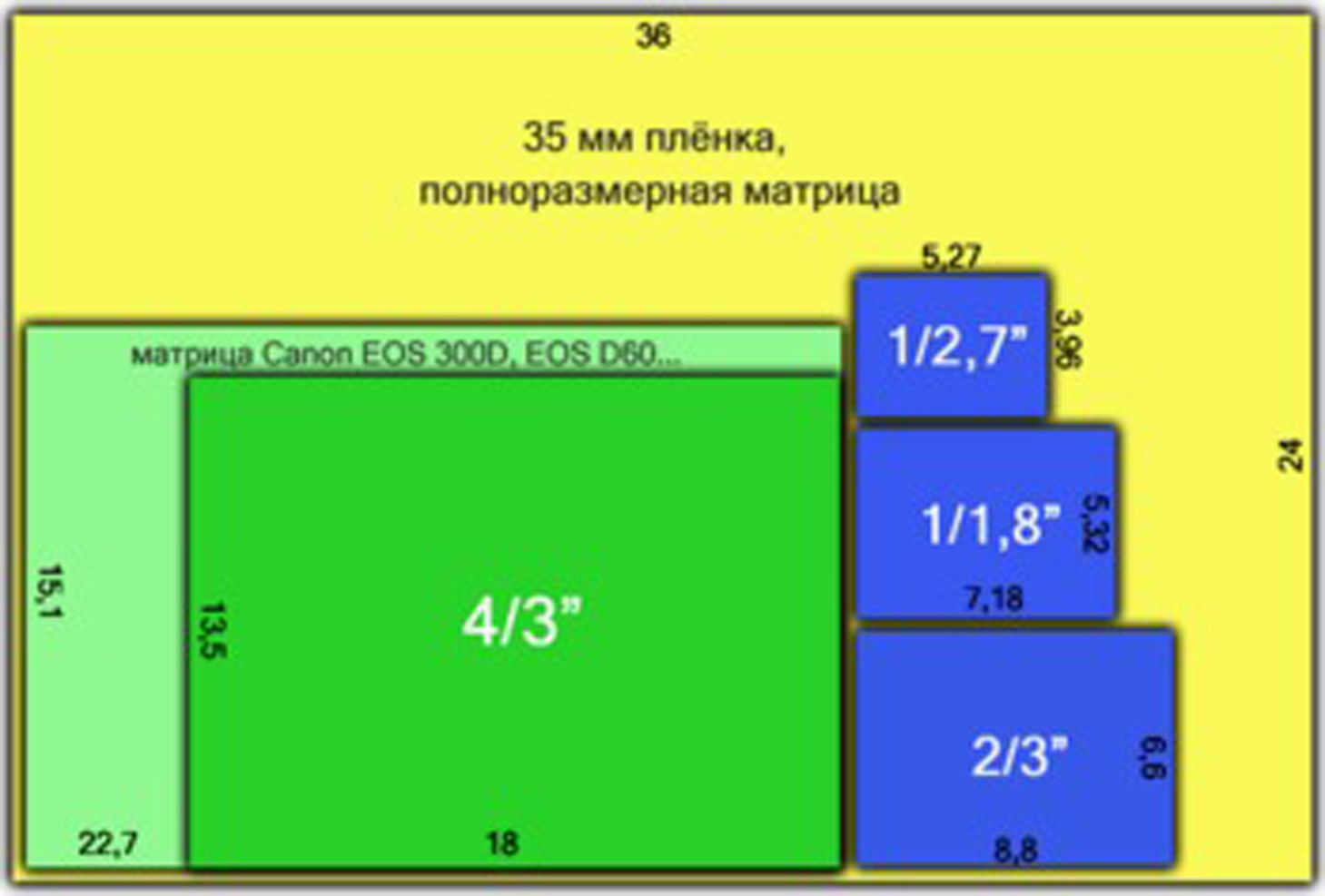 5-ти мегапиксельная матрица SONY 1/1,8″ (Olympus C-5050) шумит чуть сильнее конкурента от Panasonic (Casio QV5700). На максимальной чувствительности Nikon 5000 с его ISO 800 уступает только Olympus C-5050 с ISO 400 и лучше других аппаратов с ISO 400 и 800. Так что размер отдельной ячейки все еще важен.
5-ти мегапиксельная матрица SONY 1/1,8″ (Olympus C-5050) шумит чуть сильнее конкурента от Panasonic (Casio QV5700). На максимальной чувствительности Nikon 5000 с его ISO 800 уступает только Olympus C-5050 с ISO 400 и лучше других аппаратов с ISO 400 и 800. Так что размер отдельной ячейки все еще важен.
Дополнительно для визуальной оценки «шумности» приведены фрагменты квадратиков близкой яркости для минимальной возможной чувствительности и разных камер (яркость некоторых фрагментов немного изменена для «удобства» сравнения, у фрагмента Casio QV4000 цвета приведены к «серому», так как ручной баланс «сработал» некорректно):
Olympus C5050ZOOM ISO64 1/100 c F/2,6 | |
Nikon Coolpix 5000 ISO100 1/37 c F/4,8 | |
Canon PS G2 ISO50 1/8 c F/2,5 | |
Casio QV4000 ISO 64 (100) 1/139 c F/2 | |
Casio QV5700 ISO 50 1/93 c F/2 |
Выводы:
1.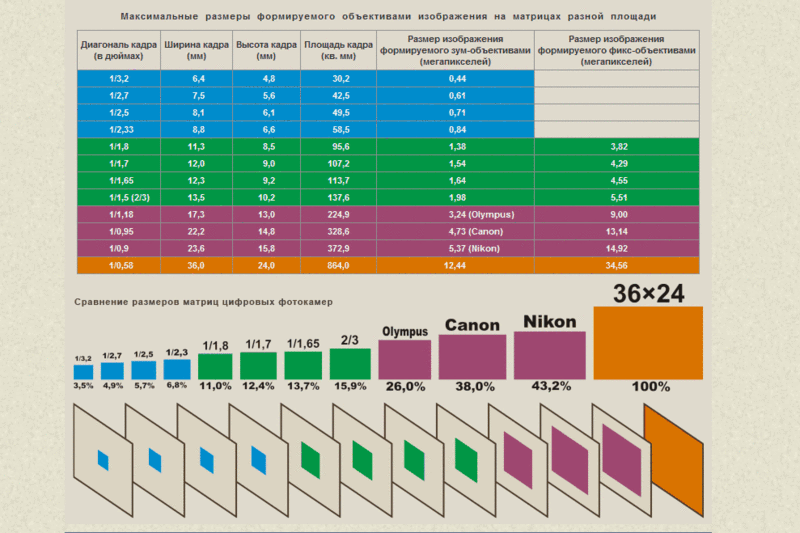 Большая матрица с большим светочувствительным элементом шумит меньше.
Большая матрица с большим светочувствительным элементом шумит меньше.
2. Шумы Canon G2 и Casio QV4000 очень похожи и если предположить, что у этих аппаратов с одинаковыми матрицами и объективами алгоритмы оцифровки разные, то надеяться на «всесилие математики» в борьбе с шумами пока рано и главное все же матрица.
3. Так как камеры собраны на базе близких по характеристикам матриц (или вообще одних и тех же), то как и в случае с пленкой выбирать следует (в одном классе) тот фотоаппарат, который устраивает вас функционально и просто вам «по душе».
Таблица характеристик матриц цифровых фотоаппаратов
От редакции сайта Vt-tech.eu
Автор данной статьи — Владимир Медведев. Статья была опубликована на личном сайте автора по адресу:
vladimirmedvedev.com/dpi.html
Однако, автор решил полностью переделать сайт и статья пропала.
Статья очень хорошо и доступно раскрывает тему дифракции при высоких значениях диафрагмы, поэтому редакция сайта Vt-Tech никак не могла пройти мимо. Мы извлекли статью из архивов кэширующих сайтов и выложили здесь.
Мы извлекли статью из архивов кэширующих сайтов и выложили здесь.
При экспорте статьи немного пострадали картинки: не все изображения из первоначальной статьи доступны.
Надеемся, что автор статьи не будет возражать против размещения её здесь.
Кто здесь
Эту таблицу я сделал уже много лет назад, для наглядного сравнения цифровых фотоаппаратов. В те годы было много путаницы даже с понятием «кропа» и «полного формата», не говоря уже про компактные и среднеформатные аппараты. Скудная информация была разбросана по многочисленным сайтам производителей фототехники, и сравнить камеры наглядно было практически невозможно. Всё это вводило в заблуждение многих фотолюбителей, разжигая яростные споры на профильных форумах.
Чтобы как-то упорядочить ситуацию и привести к одному знаменателю любые камеры — от мыльниц до среднеформатных камер, я решил использовать понятие плотности пикселей — DPI (хотя, возможно, будет правильней сказать ppi). Почему я выбрал именно этот параметр, который раньше нигде не использовался для этого? Просто потому, что имевшаяся в открытом доступе информация, позволяла рассчитывать его идеально точно, без погрешностей. Зная длину и ширину матрицы, а также количество пикселей, я мог без труда, абсолютно точно рассчитать их плотность. В качестве бонуса, понятие плотности пикселей, позволило сравнить матрицу любого размера с разрешением сканов с плёнки (DPI цифрового фотоаппарата и установленное DPI во время сканирования — по сути, одно и то же).
Зная длину и ширину матрицы, а также количество пикселей, я мог без труда, абсолютно точно рассчитать их плотность. В качестве бонуса, понятие плотности пикселей, позволило сравнить матрицу любого размера с разрешением сканов с плёнки (DPI цифрового фотоаппарата и установленное DPI во время сканирования — по сути, одно и то же).
Удобная в использовании, наглядная таблица, позволила двигаться дальше, по пути познания технических характеристик матриц, и, со временем, обросла массой дополнительных «полезностей». Сегодня в таблице собраны самые разные параметры, имеющие отношение к матрицам цифровых фотоаппаратов. Это и размер пикселя, и точный кроп-фактор, и площадь матрицы, и дифракционное ограничение диафрагмы. С помощью этой таблицы можно легко отслеживать тренды развития фототехники, прогнозировать грядущие изменения или просто выбирать камеру.
Разобраться в многочисленных параметрах таблицы сходу не так просто. Помочь фотографу в этом должны специальные статьи, сопровождающие таблицу, раскрывающие её особый смысл.
Приятного чтения!
Часть первая. Увеличивает ли кроп-фактор способность объективов «приближать»?
Поскольку я занимаюсь фотографией дикой природы, часто бывает просто невозможно подойти ближе к объекту съёмки (из-за риска испугать животное или птицу). И тут во всесь рост встаёт проблема нехватки фокусного расстояния объективов (говоря простым языком — способности оптики «приближать удалённые объекты»). На заре цифровой фотографии, было крайне распространено мнение, что камеры с «кропнутой» матрицей увеличивают фокусное расстояние объективов в кроп раз. Тут я постараюсь объяснить, почему неправильно так думать.
Сейчас у меня есть две камеры. Одна полноформатная — Canon EOS 5D Mark II, вторая с кроп-фактором 1,6х — Canon EOS 20D. Кроп-фактор 1,6, означает, что диагональ матрицы 20D в 1,6 раза меньше, чем диагональ матрицы 5D MarK II. 43mm разделить на 27mm равно 1,6.
С кроп-фактором разобрались. Матрица уменьшилась. Но оптика то осталась прежней. Объектив, например, 300мм подходит как к 20D, так и к 5D Mark II. Что будет, если один и тот же кадр снять на 5D Mk II и на 20D? Самая наглядная и точная метафора — взять большой напечатанный кадр, и вырезать из него середину ножницами. Какая разница, резать матрицу или уже готовый кадр? Вот так:
Что будет, если один и тот же кадр снять на 5D Mk II и на 20D? Самая наглядная и точная метафора — взять большой напечатанный кадр, и вырезать из него середину ножницами. Какая разница, резать матрицу или уже готовый кадр? Вот так:
Конечно, на вырезанном кадре птица выглядит крупнее. Часто, начинающими фотографами, это свойство кропа ошибочно воспринимается как плюс. Но на самом деле, плюсом вовсе не является. Зачем спешить, и «вырезать кадр» до съёмки? А если птица подлетит ближе, или нам захочется вырезать не середину, а край снимка? На полноформатной матрице мы можем резать как угодно, а можем вообще не резать. А вот кроп вариантов уже не оставляет. Вылезшие за край кадра крылья уже не вернуть, и потенциально хороший снимок отправляется в корзину.
примеры основных кроп-факторов: 1.3х, 1.6х и 2х
Спорить, что лучше, кроп или полный формат я тут не стану. Кроп может быть дешевле или быстрее. Тут у каждого своё решение. Вместо ненужных споров, предлагаю ответить на вопрос, какая характеристика камеры может по-настоящему способствовать качественному приближению? И ответ прост — плотность пикселей (столбик dpi в таблице). Для того, чтобы понять, почему это так, давайте рассмотрим ещё один пример из жизни. В этот раз, для удобства, возьмём две полноформатные камеры — 5D и 5D Mark II. Особо подчеркну, что для конечного результата совершенно не важно, полный формат у нас или кроп, тут играет роль только один параметр — плотность пикселей. У 5D это 3101 dpi, у 5D Mark II — 3955 dpi.
Для того, чтобы понять, почему это так, давайте рассмотрим ещё один пример из жизни. В этот раз, для удобства, возьмём две полноформатные камеры — 5D и 5D Mark II. Особо подчеркну, что для конечного результата совершенно не важно, полный формат у нас или кроп, тут играет роль только один параметр — плотность пикселей. У 5D это 3101 dpi, у 5D Mark II — 3955 dpi.
Представьте сафари: яркий солнечный день, низкая чувствительность ISO, отличная оптика. И вдруг мы видим дикого леопарда в 100 метрах от нас. Делаем снимок, и зверь скрывается. 100 метров — это далеко. Для того, чтобы кадр хорошо смотрелся, нам волей-неволей придётся сильно кадрировать, оставив 1/10 от полного кадра (для простоты подсчёта). Математика подсказывает, что кадр с камеры 5D (12мп) после кадрирования будет состоять из 1,2мп (12 разделить на 10), что очень мало и не годится для качественной печати. А вот снимок с 5D MII (21мп) будет состоять из 2,1 мп, что уже значительно лучше! И я ещё раз хочу подчеркнуть — совершенно не важно, кроп у нас, или полный формат. 20D, у которой плотность 3955dpi (как и у 5D Mark II), аналогичный кадр, в тех-же самых условиях, тоже состоял бы из 2,1 мп. Несмотря на то, что матрица там всего 8 мегапикселей. Тут играет роль только плотность пикселей.
20D, у которой плотность 3955dpi (как и у 5D Mark II), аналогичный кадр, в тех-же самых условиях, тоже состоял бы из 2,1 мп. Несмотря на то, что матрица там всего 8 мегапикселей. Тут играет роль только плотность пикселей.
Леопарда снять одновременно с двух камер не представляется возможным, поэтому я попробовал тест попроще, чтобы наглядно показать разницу от плотности пикселей. Два тестовых кадра, были сняты со штатива, с одинакового расстояния, с одинаковой оптики, с одинаковым фокусным расстоянием:
полный кадр выглядел так
при очень сильном приближении становится видна разница
Это не сравнение 450D против 1D Mark III. Это сравнение 3514 dpi против 4888 dpi. В этих условиях, аналогичный результат будет на любой другой паре камер с подобной плотностью пикселей. Просто когда я писал статью, у меня были именно эти две камеры, вот и всё.
Ps:
- Тесты проводились в хороших условиях, и рассматривались под большим увеличением.
 В реальной жизни, скорее всего, разница будет заметна ещё меньше. Стоит оно того или нет, решать только вам.
В реальной жизни, скорее всего, разница будет заметна ещё меньше. Стоит оно того или нет, решать только вам. - Разумеется, качество 21 мегапикселя 5D Mark II, в сравнении с 12 мегапикселями 5D, будет заметно не только при сильном кадрировании. Надеюсь, это и так всем понятно.
Часть вторая. Меньше пиксель — больше шум
Из первой части можно сделать вывод — давайте наращивать плотность пикселей, что бы картинка была лучше. Но не всё так просто. Чем больше плотность пикселей, тем меньше площадь каждого конкретного пикселя (такой столбик тоже есть в таблице). Чем меньше площадь пикселя, тем меньше фотонов света он улавливает. Фотоны — это полезный сигнал. Чем их меньше, тем хуже соотношение сигнал/шум, тем хуже чувствительность камеры.
Скажу просто — камеры, которые мне приходилось тестировать, с размером пикселя менее 6 микрон, имеют плохую чувствительность и более высокий шум. Это моё мнение, мой опыт. Пока что никаких исключений в этом правиле я не видел. Возможно, когда-нибудь, технологии позволят делать новые камеры более чувствительными, но пока так. Возникает вопрос, что выбрать? Плотность пикселей или чувствительность? Тут всем придётся искать свой собственный ответ. Кому интересно моё мнение, смотрите следующие два абзаца, но… никому его не навязываю. 🙂
Возможно, когда-нибудь, технологии позволят делать новые камеры более чувствительными, но пока так. Возникает вопрос, что выбрать? Плотность пикселей или чувствительность? Тут всем придётся искать свой собственный ответ. Кому интересно моё мнение, смотрите следующие два абзаца, но… никому его не навязываю. 🙂
Я проанализировал свои снимки, за последние несколько лет, размышляя, может ли большая плотность пикселей увеличить качество моих снимков. Результат оказался очень неожиданным: снимков, качество которых можно улучшить за счёт плотности пикселей, оказалось крайне мало. Помимо моих кривых рук, виной тому стали многие естественные факторы — шумы, шевелёнка, качество оптики, «воздух», не точный АФ и пр. Причём, 90% снимков, которые можно было бы улучшить повышенной плотностью пикселей, в улучшении и не нуждались — все они и так обладали достаточным качеством.
Показательно, что большая часть некачественных фотографий страдала из-за недостатка чувствительности. Шевелёнка и шумы мне, как фотографу дикой природы, сейчас мешают гораздо сильнее.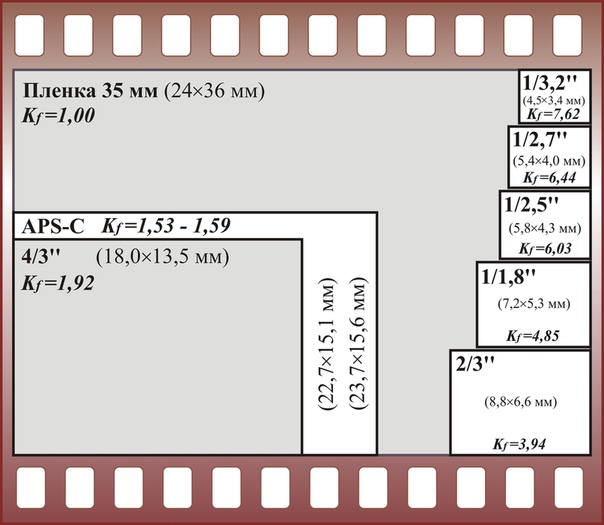 16-25 мегапикселей на полном формате — мой идеал на сегодняшний день.
16-25 мегапикселей на полном формате — мой идеал на сегодняшний день.
Также не стоит забывать про ДД — динамический диапазон, который очень тесно связан с шумами, т.к. они ограничивают его в тенях. Меньше пиксель — меньше и ДД. Выводы тут каждый сам для себя сделает. А тех, кому важнее окажется плотность пикселей, я хочу предупредить об ещё одном коварном враге, который будет вечно подстерегать Вас, и от которого Вам не скрыться. По крайней мере в этой Вселенной. Это дифракция…
Часть третья. Дифракция в фотографии. Теория
Для этой части моей статьи все рисунки взяты из
замечательного учебного пособия про дифракцию:
Tutorials: difraction & photography. Очень рекомендую
его всем, кто хочет глубоко разобраться в этой теме.
В этой части матрица ни причём, а отдуваться всё равно приходится. За физику. Какое отношение имеет дифракция к матрице цифрового фотоаппарата? Никакого. Но давайте рассмотрим, что же мы имеем ввиду под словом дифракция, когда говорим о головной боли фотографов?
Если не вдаваться в подробности, то дифракция — это физическое явление, которое мешает нам сильно закрывать диафрагму, снижая качество получаемого изображения.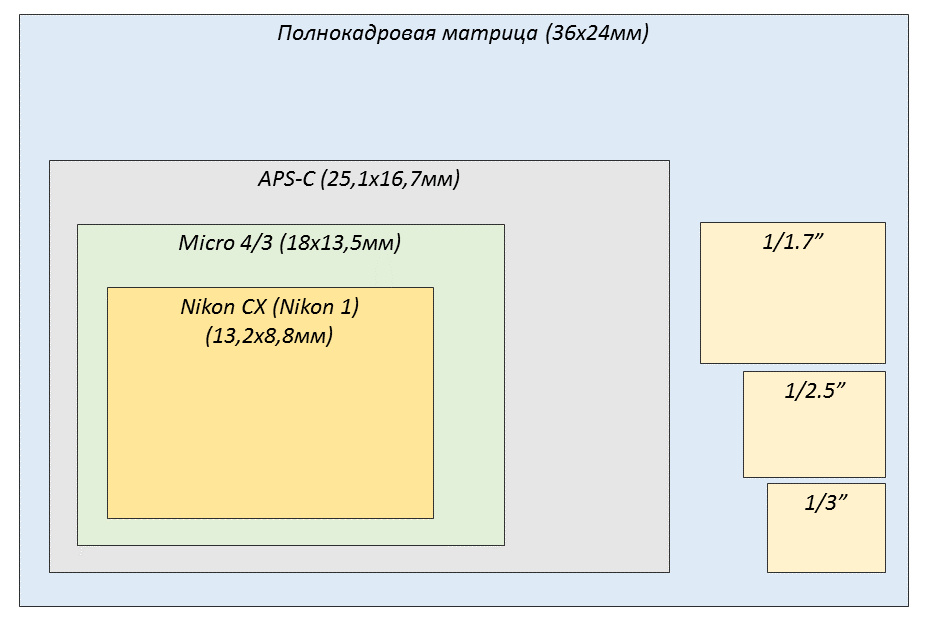
Если рассмотреть причины дифракции, то мы увидим, что появляется она при прохождении света через диафрагму. После прохождения диафрагмы, лучи идут уже не столь прямо, как нам хотелось бы, а немного «расслаиваются», расходятся в стороны. В результате каждый лучик образует на поверхности матрицы не просто точку, а «кружок и круги по воде» — дифракционные кольца, или, как это ещё называют диск Эри (по фамилии учёного, английского астронома — George Biddell Airy):
Разумеется, что, в отличие от хорошо сфокусированной точки, подобные диски могут залезть на соседние пиксели, если те расположены достаточно плотно. А когда они лезут на соседние пиксели, мы прощаемся с хорошей резкостью.
Давайте рассмотрим это явление на примере. Зная размер пикселей, мы без труда построим сетку, обозначающую границы пикселей (пунктиром). Далее по формуле мы вычисляем диаметр диска Эри и для упрощения представляем его в виде пятна света. И попробуем наложить диски Эри, характерные для самых распространённых диафрагм, на нашу сетку. Для примера я взял размер пикселя камеры 5D MarkII, а значения диафрагм указаны под каждым рисунком:
Для примера я взял размер пикселя камеры 5D MarkII, а значения диафрагм указаны под каждым рисунком:
Как вы видите, при неизменной сетке пикселей кружок Эри растёт. При f/16 он уже значительно залезает на соседние пиксели, что в реальной жизни будет размывать картинку, не давая нам попиксельной резкости. А при f/22 этот диск занимает почти всю площадь 9 пикселей!
Зная размеры этого кружка, я могу рассчитать максимально закрытую диафрагму, после которой дальнейшее закрытие, будет ухудшать фотографию. Этот параметр мой коллега с the-digital-picture.com называет DLA (diffraction limited aperture), что соответствует русскому термину ДОД (дифракционное ограничение диафрагмы). Однако мои расчёты числового значения этого параметра несколько отличаются от вычислений автора вышеуказанного сайта. Например, в своей формуле он, видимо, каким-то образом учитывает и размер всей матрицы (в частности, при равной плотности пикселей, значения DLA 40D (f/9.3) и 1D MarkIV (f/9.1) различаются). Это, конечно же, не может быть верным, когда мы говорим о дифракции на уровне пикселей. Впрочем, наши результаты не сильно расходятся, так что разницей можно принебречь. К тому же, в силу сочетания очень многих факторов (нечеткость границ диска, сложная структура ячеек матрицы и пр.), невозможно с абсолютной точностью назвать величину DLA, после которой начинает наблюдаться деградация изображения.
Это, конечно же, не может быть верным, когда мы говорим о дифракции на уровне пикселей. Впрочем, наши результаты не сильно расходятся, так что разницей можно принебречь. К тому же, в силу сочетания очень многих факторов (нечеткость границ диска, сложная структура ячеек матрицы и пр.), невозможно с абсолютной точностью назвать величину DLA, после которой начинает наблюдаться деградация изображения.
Итак, давайте посмотрим, как это работает. Для 5D MarkII (как и для 20D), DLA составляет f/10,8, что очень близко к рисунку выше с подписью f/11. В то же время, для Canon 1D (всего 4 mp, — самые крупные ячейки матрицы среди всех камер Canon), этот параметр составляет f/19,1. Давайте закроем диафрагму до f/16, и посмотрим, как будет выглядеть диск Эри, спроецированный на сетку пикселей 1D и на сетку 5D MarkII (или 1Ds MarkIII или 20D):
Как видно из этого примера, что позволено Юпитеру, не позволено быку. При съёмке на 1D мы легко можем закрыть диафрагму до f/16, а на 5D Mark II это приведёт к снижению возможной детализации.
Часть четвёртая. Дифракция в фотографии. Практика
Выше была лишь сухая теория. Она абсолютно верна, но не учитывает того, что оптика очень часто не способна выдать достаточной детализации, на диафрагмах уже DLA. Так как же дело обстоит на практике?
Действительно, оптика не всегда даёт качество, которое позволило бы нам видеть попиксельную резкость. Более того, как мы знаем, качество изображения растёт по мере закрытия диафрагмы. Из-за этого у качественной оптики мы можем заметить ухудшение качества из-за дифракции на диафрагмах близких к DLA, а вот у плохих это может произойти на значительно позже. Однако, если ухудшение наступает на одно или даже два значения диафрагмы уже DLA, это означает, что матрица камеры с этим объективом никогда не получает достаточно детаелй. Т.е. попиксельной резкости там не будет никогда, иначе дифракцию мы бы смогли заметить на уровне числового значения DLA.
Что же мы можем наблюдать на камерах с большой плотностью пикселей? Для примера возьмём новую (на момент написания этих строк) камеру Canon EOS 7D. DLA там составляет f/7,2. Что это значит? Это значит, что 7D сможет выдать попиксельную детализацию только на диафрагмах менее 7,2. Возьмём хорошую оптику и посмотрим на результат. Для этого обратимся за помощью к ресурсу The Digital Picture. Там мы можем найти снимок специальной тестовой таблицы на камеру 7D с использованием хорошей оптики (Canon EF 200mm f/2.0L IS USM). Сравним кадр, сделанный при диафрагме 5,6 и 8. Как мы видим, резкость незначительно ухудшается — теория работает! Теперь сравним 5,6 и 11 — вот тут уже идёт заметное падение резкости, причём не только по центру, но даже в углах!
DLA там составляет f/7,2. Что это значит? Это значит, что 7D сможет выдать попиксельную детализацию только на диафрагмах менее 7,2. Возьмём хорошую оптику и посмотрим на результат. Для этого обратимся за помощью к ресурсу The Digital Picture. Там мы можем найти снимок специальной тестовой таблицы на камеру 7D с использованием хорошей оптики (Canon EF 200mm f/2.0L IS USM). Сравним кадр, сделанный при диафрагме 5,6 и 8. Как мы видим, резкость незначительно ухудшается — теория работает! Теперь сравним 5,6 и 11 — вот тут уже идёт заметное падение резкости, причём не только по центру, но даже в углах!
Весь парадокс камер с высокой плотностью пикселей, что оптике и так сложно передать значительное количество деталей, а передать значительное количество деталей на диафрагмах шире, чем f/8… боюсь это задача лишь для действительно великолепных объективов. Таких, как Canon EF 200mm f/2.0L IS USM ~ за 6000$…
В заключение, для невнимательных читателей, я хочу ещё раз подчеркнуть, что дифракция не является параметром матрицы, искажает изображение до матрицы и не зависит от марки камеры (а если и зависит, разница минимальна и я её не учитываю).
Благодарю Дмитрия (Доктор Ктулху) за помощь, оказанную в процессе редактирования текста статьи.
Таблица характеристик матриц цифровых фотоаппаратов
| Модель | Произв | Тип | Mp* | Кроп-фактор | Размер пикселя (микрон) | Площадь (мм2 ) | Размер матрицы (мм) | Размер матрицы (пикселей) | DPI | DLA** | FF*** (mp) |
| C a n o n | |||||||||||
| 1D | Kodak | CCD | 4,1 | 1.3 х | 11,6 µm | 548,2 | 28,7 x 19,1 | 2464 x 1648 | 2181 | f/19,1 | 6,4 |
| D30 | Canon | CMOS | 3,1 | 1. 6 х 6 х | 10,5 µm | 342,8 | 22,7 x 15,1 | 2160 x 1440 | 2417 | f/17,6 | 7,8 |
| 1Ds | Canon | CMOS | 11,0 | 1.0 х | 8,8 µm | 852 | 35,8 x 23,8 | 4064 x 2704 | 2883 | f/14,8 | 11,1 |
| 1D Mark II | Canon | CMOS | 8,2 | 1.3 х | 8,2 µm | 548,2 | 28,7 x 19,1 | 3504 x 2336 | 3101 | f/13,8 | 12,9 |
| 5D | Canon | CMOS | 12,7 | 1.0 х | 8,2 µm | 852 | 35,8 x 23,9 | 4368 x 2912 | 3101 | f/13,8 | 12,9 |
| 300D/D60/10D | Canon | CMOS | 6,3 | 1. 6 х 6 х | 7,4 µm | 342,8 | 22,7 x 15,1 | 3072 x 2048 | 3400 | f/12,4 | 15,5 |
| 1Ds Mark II | Canon | CMOS | 16,6 | 1.0 х | 7,2 µm | 864 | ~ 36 x 24 | 4992 x 3328 | 3514 | f/12,1 | 16,5 |
| 1D Mark III | Canon | CMOS | 10,1 | 1.3 х | 7,2 µm | 525,5 | 28,1 x 18,7 | 3888 x 2592 | 3514 | f/12,1 | 16,5 |
| 1D x | Canon | CMOS | 17,9 | 1.0 х | 6,9 µm | 864 | 36 x 24 | 5184 x 3456 | 3657 | f/11,7 | 17,9 |
| 350D/20D/30D | Canon | CMOS | 8,2 | 1. 6 х 6 х | 6,4 µm | 337,5 | 22,5 x 15,0 | 3504 x 2336 | 3955 | f/10,8 | 20,9 |
| 5D II / 1Ds III | Canon | CMOS | 21,0 | 1.0 х | 6,4 µm | 864 | ~ 36 x 24 | 5616 x 3744 | 3955 | f/10,8 | 20,9 |
| 5D III | Canon | CMOS | 22,1 | 1.0 х | 6,25 µm | 864 | 36 x 24 | 5760 x 3840 | 4064 | f/10,6 | 22,1 |
| 1000D/400D/40D | Canon | CMOS | 10,1 | 1.6 х | 5,7 µm | 328,6 | 22,2 x 14,8 | 3888 x 2592 | 4455 | f/9,6 | 26,6 |
| Canon EOS 1D Mark IV | Canon | CMOS | 16,1 | 1. 3 х 3 х | 5,7 µm | 518,9 | 27,9 x 18,6 | 4896 x 3264 | 4455 | f/9,6 | 26,6 |
| Canon EOS 450D | Canon | CMOS | 12,2 | 1.6 х | 5,2 µm | 328,6 | 22,2 x 14,8 | 4272 x 2848 | 4888 | f/8,7 | 32,0 |
| 500D, 50D | Canon | CMOS | 15,1 | 1.6 х | 4,7 µm | 332,3 | 22,3 x 14,9 | 4752 x 3168 | 5413 | f/7,9 | 39,2 |
| 7D / 60D / 600D | Canon | CMOS | 17,9 | 1.6 х | 4,3 µm | 332,3 | 22,3 x 14,9 | 5184 x 3456 | 5905 | f/7,2 | 46,7 |
| 7D Mark II | Canon | CMOS | 19. 96 96 | 1.6 х | 4,1 µm | 336 | ~ 22,4 x 15,0 (?) | 5472 x 3648 | ~ 6177 | f/6.9 | 50,3 |
| 5Ds (r) | Canon | CMOS | 50,3 | 1.0 х | 4,1 µm | 864 | 36 x 24 | 8688 x 5792 | 6130 | f/6.9 | 50,3 |
| N i k o n | |||||||||||
| D1/D1H | Sony | CCD | 2,6 | 1.5 х | 11,9 µm | 367,4 | 23,7 x 15,5 | 2000 x 1312 | 2143 | f/20 | 6,2 |
| D2H | Nikon | JFET | 4,0 | 1.5 х | 9,6 µm | 367,4 | 23,7 x 15,5 | 2464 x 1632 | 2641 | f/16,1 | 9,3 |
| D1X**** | Sony | CCD | 5,3 | 1. 5 х 5 х | 5,9/11,9 | 369,7 | 23,7 x 15,6 | 4028 x 1324 | — | — | — |
| D700/D3/D3s | ? | CMOS | 12.1 | 1.0 х | 8,4 µm | 860,4 | 36,0 x 23,9 | 4256 x 2832 | 3003 | f/14,1 | 12,2 |
| D4 | ? | CMOS | 16,2 | 1.0 х | 7,3 µm | 860,4 | 36,0 x 23,9 | 4928 x 3280 | 3476 | f/12,4 | 16,2 |
| D40/D50/D70/D100 | Sony | CCD | 6,0 | 1.5 х | 7,8 µm | 367,4 | 23,7 x 15,5 | 3008 x 2000 | 3237 | f/13,1 | 14,0 |
| D3000/D40x/D60/D80/D200 | Sony | CCD | 10,0 | 1. 5 х 5 х | 6,1 µm | 372,9 | 23,6 x 15,8 | 3872 x 2592 | 4167 | f/10,3 | 23,4 |
| D3X | ? | CMOS | 24,4 | 1.0 х | 5,9 µm | 861,6 | 35,9 x 24 | 6048 x 4032 | 4279 | f/9,9 | 24,4 |
| D5000 / D90 | Sony | CMOS | 12.2 | 1.5 х | 5,4 µm | 369,7 | 23,7 x 15,6 | 4288 x 2848 | 4637 | f/9 | 28,8 |
| D300 (s) / D2X (s) | Sony | CMOS | 12.2 | 1.5 х | 5,4 µm | 369,7 | 23,7 x 15,6 | 4288 x 2848 | 4637 | f/9 | 28,8 |
| D800 (e) | ? | CMOS | 36,2 | 1. 0 х 0 х | 4,9 µm | 861,6 | 35,9 x 24 | 7360 x 4912 | 5207 | f/8,2 | 36,3 |
| D7000/5100 | Sony | CMOS | 16.1 | 1.5 х | 4,8 µm | 370,5 | 23,6 x 15,7 | 4928 x 3264 | 5303 | f/8,1 | 37,4 |
| S o n y | |||||||||||
| A 100/200/230/300/330 | Sony | CCD | 10.0 | 1.5 х | 6,1 µm | 372,9 | 23,6 x 15,8 | 3872 x 2592 | 4167 | f/10,2 | 23,3 |
| A900 / A850 | Sony | CMOS | 24,4 | 1.0 х | 5,9 µm | 861,6 | 35,9 x 24 | 6048 x 4032 | 4279 | f/9,9 | 24,4 |
| A500 | Sony | CMOS | 12. 2 2 | 1.5 х | 5,7 µm | 366,6 | 23,5 x 15,6 | 4272 x 2848 | 4617 | f/9,6 | 28,6 |
| A700 | Sony | CMOS | 12.2 | 1.5 х | 5,5 µm | 368,2 | 23,5 x 15,6 | 4288 x 2856 | 4635 | f/9,2 | 28,8 |
| A350/A380 | Sony | CCD | 14.0 | 1.5 х | 5,1 µm | 369 | 23,5 x 15,7 | 4592 x 3056 | 4963 | f/8,6 | 33,0 |
| Sony A550 | Sony | CMOS | 14.0 | 1.5 х | 5,1 µm | 365 | 23,4 x 15,6 | 4592 x 3056 | 4984 | f/8,6 | 33,3 |
| SLT-A57/35/55/A580 | Sony | CMOS | 16,0 | 1.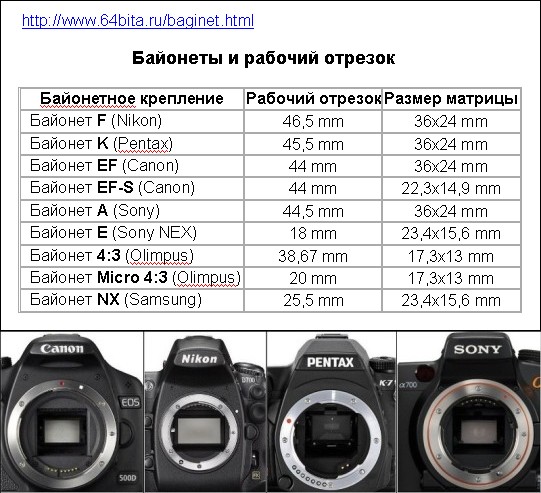 5 х 5 х | 4,8 µm | 366,6 | 23,5 x 15,6 | 4912 x 3264 | 5309 | f/8,1 | 37,7 |
| SLT-A77 / A65 / NEX-7 | Sony | CMOS | 24,0 | 1.5 х | 3,9 µm | 366,6 | 23,5 x 15,6 | 6000 x 4000 | 6485 | f/6,5 | 54 |
| F u j i f i l m***** | |||||||||||
| S2 Pro | Fujifilm | CCD | 6,1 | 1.6 х | 7,6 µm | 356,5 | 23 x 15.5 | 3024 x 2016 | 3340 | f/12,8 | 14,9 |
| S3/S5 Pro | Fujifilm | CCD | 6,1 | 1.6 х | 7,6 µm | 356,5 | 23 x 15.5 | 3024 x 2016 | 3340 | f/12,8 | 14,9 |
| P e n t a x | |||||||||||
| K100D (Super) /K110D | Sony | CCD | 6,0 | 1. 5 х 5 х | 7,8 µm | 368,95 | 23,5 x 15,7 | 3008 x 2008 | 3251 | f/13,1 | 14,2 |
| K10D/K200D/K2000 | Sony | CCD | 10,0 | 1.5 х | 6,1 µm | 369 | 23,5 x 15,7 | 3872 x 2592 | 4185 | f/10,3 | 23,6 |
| 645D | Kodak | CCD | 39,5 | 0.7 х | 6,1 µm | 1452 | 44 x 33 | 7264 x 5440 | 4193 | f/10,2 | 24,5 |
| K-r | ? | CMOS | 12.2 | 1.5 х | 5,5 µm | 372,9 | 23,6 x 15,8 | 4288 x 2848 | 4615 | f/9,3 | 28,3 |
| K20D/K-7 | Samsung | CMOS | 14.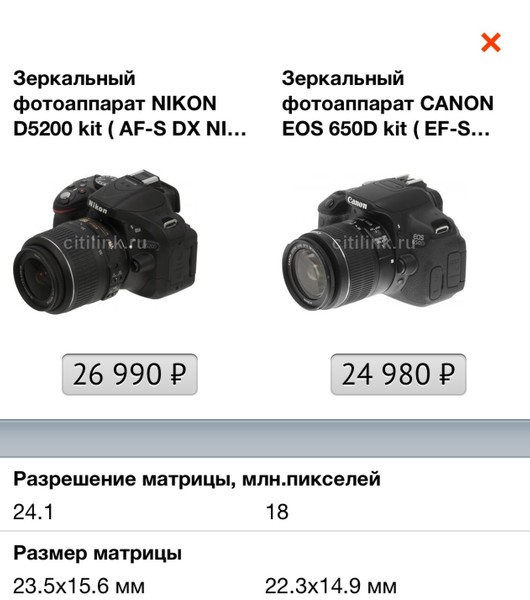 5 5 | 1.5 х | 5,0 µm | 365 | 23,4 x 15,6 | 4672 x 3104 | 5071 | f/8,4 | 34,5 |
| K-5 | Sony | CMOS | 16.1 | 1.5 х | 4,8 µm | 370,5 | 23,6 x 15,7 | 4928 x 3264 | 5303 | f/8,1 | 37,4 |
| S i g m a****** | |||||||||||
| SD14/SD15/DP1/DP2 | Foveon | CMOS | 4,7 | 1.7 х | 7,8 µm | 285,7 | 20,7 x 13,8 | 2640 x 1760 | 3239 | f/13,1 | 14,1 |
| SD1 (m) | Foveon | CMOS | 15,4 | 1.5 х | 5 µm | 384 | 24 x 16 | 4800 x 3200 | 5080 | f/8,5 | 34,6 |
| S a m s u n g | |||||||||||
| GX-20 | Samsung | CMOS | 14. 6 6 | 1.5 х | 5,0 µm | 365 | 23,4 x 15,6 | 4688 x 3120 | 5089 | f/8,4 | 34,6 |
| NV40 | ? | CCD | 10,1 | 6,0 x | 1,7 µm | 28,2 | 6,13 x 4,60 | 3648 x 2736 | 15116 | f/2,9 | 306 |
| O l y m p u s | |||||||||||
| E400/410/420/450 | Matsushita | NMOS | 9.98 | 2.0 х | 4,7 µm | 225 | 17,3 x 13,0 | 3648 x 2736 | 5356 | f/7,9 | 38,4 |
| E510/520/E3 | Matsushita | NMOS | 9.98 | 2.0 х | 4,7 µm | 225 | 17,3 x 13,0 | 3648 x 2736 | 5356 | f/7,9 | 38,4 |
| E620/E30/E5 | Matsushita | NMOS | 12. 2 2 | 2.0 х | 4,3 µm | 225 | 17,3 x 13,0 | 4032 x 3024 | 5919 | f/7,3 | 48,7 |
| E-M5 | Matsushita | NMOS | 15.9 | 2.0 х | 3,7 µm | 225 | 17,3 x 13,0 | 4608 x 3456 | 6765 | f/6,3 | 63,7 |
| L e i c a | |||||||||||
| M8 | Kodak | CCD | 10 | 1.3 x | 6,8 µm | 479,7 | 26,8 x 17,9 | 3936 x 2630 | 3731 | f/11,4 | 18,1 |
| M9 | Kodak | CCD | 18,1 | 1.0 x | 6,8 µm | 864 | 36 x 24 | 5212 x 3472 | 3731 | f/11,4 | 18,1 |
| S2 | Kodak | CCD | 37. 5 5 | 0,8 x | 6,0 µm | 1350 | 45 x 30 | 7500 x 5000 | 4230 | f/10 | 22,4 |
| H a s s e l b l a d | |||||||||||
| h4DII-31 | Kodak | CCD | 31,6 | 0,8 x | 6,8 µm | 1463 | 44,2 x 33,1 | 6496 x 4872 | 3731 | f/11,4 | 18,1 |
| h4DII-39 | Kodak | CCD | 39,0 | 0,7 x | 6,8 µm | 1807 | 49,1 x 36,8 | 7212 x 5412 | 3731 | f/11,4 | 18,1 |
| h4DII-50 | Kodak | CCD | 50,1 | 0,7 x | 6,0 µm | 1807 | 49,1 x 36,8 | 8176 x 6132 | 4230 | f/10 | 22,4 |
| P h o n e s | |||||||||||
| iPhone 3Gs | OV3650 | CMOS | 3,1 | 9.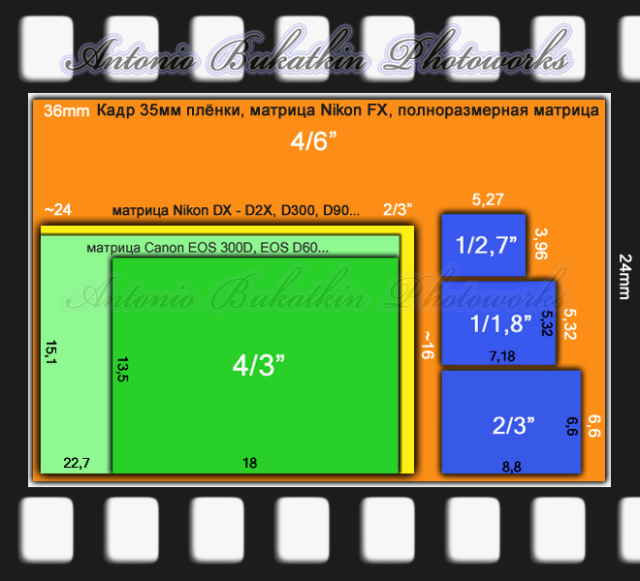 73 x 73 x | 1,75 µm | 9,8 | 3,63 x 2,71 | 2048 x 1536 | 14343 | f/2,95 | 275 |
| iPhone 4 | OV5650 | CMOS | 5,0 | 7,64 x | 1,75 µm | 15,7 | 4,59 x 3,42 | 2592 x 1936 | 14343 | f/2,95 | 275 |
| iPhone 4s | OmniVision | CMOS | 8,0 | 7,64 x | 1,4 µm | 15,7 | 4,59 x 3,42 | 3264 x 2448 | 18100 | f/2,37 | 438,7 |
| Nokia 808 | ? | CMOS | 41,4 | 3,5 x | 1,4 µm | 81 | 10,8 x 7,5 | 7728 x 5368 | 18100 | f/2,37 | 438,7 |
В эту таблицу я вложил много сил и своего времени, её копирование запрещено (с) VladimirMedvedev. com
com
Примечания:
1 Mp — количество мегапикселей в фотографии
2 DLA (diffraction limited aperture) — ДОД (дифракционное ограничение диафрагмы). Самая узкая диафрагма при которой возможна попиксельная резксть (подробнее см раздел Дифракиция, перед таблицей).
3 36х24 mp — показывает предполагаемое количество пикселей на полноформатной матрице, сделанной по технологии рассматриваемой камеры. Т.е., например, если сделать полноформатную матрицу на основе Canon 50D, то она будет на 39,2 mp.
4 Пиксели Nikon D1x прямоугольные. Реальные 5 mp, получаемые с матрицы растягивались в 10 mp фотографию. Рассчитывать dpi и dla для такой техники смысла нет.
5 Fujifilm — Подсчитывая dpi сенсора у камер Fujifilm с нестандартной матрицей (с ячейками двух типов), учитывались только основные пиксели. Из-за структуры матрицы, было бы не правильно считать и основные и дополнительные пиксели. Основные пиксели занимают практически весь полезный объём, а маленькие, дополнительные, — лишь небольшие ячейки между ними (для более подробной информации смотрите официальный сайт Fujifilm).
6 Sigma — Матрицы Foveon, которые используются в камерах компании Sigma, состоят из трёх слоёв (RGB) и, в отличае от других камер, каждый пиксель на фотографии формируется из трёх пикселей матрицы. Это происходит потому, что пиксели расположены один над одним и не несут дополнительной информации о яркости (только о цвете). Именно поэтому, при матрице в ~ 14 mp, фотографии получаются всего 4 mp. Плотность пикслов рассчитывается для одного слоя.
PS Не могу не отметить, что на самом деле, фотоприёмник занимает далеко не всю площадь пикселя, некоторое место приходится уделять также и, так называемой, обвязке. Для того, чтобы увеличить полезную площадь, производители создают специальные собирающие микро-линзы на матрице:
Чем с большей площади собирают свет микролинзы, тем более эффективной должна быть, в теории, работа матрицы, и тем меньше должно быть шумов. Но это пока только в теории…
CCD или CMOS? Что лучше?
В рубрику «Видеонаблюдение (CCTV)» | К списку рубрик | К списку авторов | К списку публикаций
Сенсор изображения является важнейшим элементом любой видеокамеры. Сегодня практически во всех камерах используются датчики изображения CCD или CMOS. Оба типа датчика выполняют задачу преобразования изображения, построенного на сенсоре объективом, в электрический сигнал. Однако вопрос, какой датчик лучше, до сих пор остается открытым
Сегодня практически во всех камерах используются датчики изображения CCD или CMOS. Оба типа датчика выполняют задачу преобразования изображения, построенного на сенсоре объективом, в электрический сигнал. Однако вопрос, какой датчик лучше, до сих пор остается открытым
Н.И. Чура
Технический консультант
ООО «Микровидео Группа»
CCD является аналоговым датчиком, несмотря на дискретность светочувствительной структуры. Когда свет попадает на матрицу, в каждом пикселе накапливается заряд или пакет электронов, преобразуемый при считывании на нагрузке в напряжение видеосигнала, пропорциональное освещенности пикселей. Минимальное количество промежуточных переходов этого заряда и отсутствие активных устройств обеспечивают высокую идентичность чувствительных элементов CCD.
CMOS-матрица является цифровым устройством с активными чувствительными элементами (Active Pixel Sensor). С каждым пикселем работает свой усилитель, преобразующий заряд чувствительного элемента в напряжение. Это дает возможность практически индивидуально управлять каждым пикселем.
Это дает возможность практически индивидуально управлять каждым пикселем.
Эволюция CCD
С момента изобретения CCD лабораторией Белла (Bell Laboratories, или Bell Labs) в 1969 г. размеры сенсора изображения непрерывно уменьшались. Одновременно увеличивалось число чувствительных элементов. Это естественно вело к уменьшению размеров единичного чувствительного элемента (пикселя), а соответственно и его чувствительности. Например, с 1987 г. эти размеры сократились в 100 раз. Но благодаря новым технологиям чувствительность одного элемента (а следовательно, и всей матрицы) даже увеличилась.
Что позволило доминировать
С самого начала CCD стали доминирующими сенсорами, поскольку обеспечивали лучшее качество изображения, меньший шум, более высокую чувствительность и большую равномерность параметров пикселей. Основные усилия по совершенствованию технологии были направлены на улучшение характеристик CCD.
Как растет чувствительность
По сравнению с популярной матрицей Sony HAD стандартного разрешения (500х582) конца 1990-х гг. (ICX055) чувствительность моделей более совершенной технологии Super HAD выросла почти в 3 раза (ICX405) и Ex-view HAD – в 4 раза (ICX255). Причем для черно-белого и цветного варианта.
(ICX055) чувствительность моделей более совершенной технологии Super HAD выросла почти в 3 раза (ICX405) и Ex-view HAD – в 4 раза (ICX255). Причем для черно-белого и цветного варианта.
Для матриц высокого разрешения (752х582) успехи несколько менее впечатляющие, но если сопоставлять модели цветного изображения Super HAD с самыми современными технологиями Ex-view HAD II и Super HAD II, то рост чувствительности составит в 2,5 и 2,4 раза соответственно. И это несмотря на уменьшение размеров пикселя почти на 30%, поскольку речь идет о матрицах самого современного формата 960H с увеличенным количеством пикселей до 976х582 для стандарта PAL. Для обработки такого сигнала Sony предлагает ряд сигнальных процессоров Effio.
Добавилась ИК-составляющая
Одним из эффективных методов роста интегральной чувствительности является расширение спектральных характеристик чувствительности в область инфракрасного диапазона. Это особенно характерно для матрицы Ex-view. Добавление ИК-составляющей несколько искажает передачу относительной яркости цветов, но для черно-белого варианта это не критично. Единственная проблема возникает с цветопередачей в камерах «день/ночь» с постоянной ИК-чувствительностью, то есть без механического ИК-фильтра.
Добавление ИК-составляющей несколько искажает передачу относительной яркости цветов, но для черно-белого варианта это не критично. Единственная проблема возникает с цветопередачей в камерах «день/ночь» с постоянной ИК-чувствительностью, то есть без механического ИК-фильтра.
Развитие этой технологии в моделях Ex-view HAD II (ICX658AKA) в сравнении с предыдущим вариантом (ICX258AK) обеспечивает рост интегральной чувствительности всего на 0,8 дБ (с 1100 до 1200 мВ) с одновременным увеличением чувствительности на длине волны 950 нм на 4,5 дБ. На рис. 1 приведены характеристики спектральной чувствительности этих матриц, а на рис. 2 – отношение их интегральной чувствительности.
Оптические инновации
Другим методом роста чувствительности CCD являются увеличение эффективности пиксельных микролинз, светочувствительной области и оптимизация цветовых фильтров. На рис. 3 представлено устройство матриц Super HAD и Super HAD II, показывающее увеличение площади линзы и светочувствительной области последней модификации.
Дополнительно в матрицах Super HAD II значительно увеличено пропускание светофильтров и их устойчивость к выцветанию. Кроме того, расширено пропускание в коротковолновой области спектра (голубой), что улучшило цветопередачу и баланс белого.
На рис. 4 представлены спектральные характеристики чувствительности матриц Sony 1/3″ Super HAD (ICX229AK) и Super HAD II (ICX649AKA).
CCD: уникальная чувствительность
В совокупности перечисленных мер удалось добиться значительных результатов по улучшению характеристик CCD.
Сравнить характеристики современных моделей с более ранними вариантами не представляется возможным, поскольку тогда не производились цветные матрицы широкого применения даже типового высокого разрешения. В свою очередь, сейчас не производятся черно-белые матрицы стандартного разрешения по новейшим технологиям Ex-view HAD II и Super HAD II.
В любом случае по чувствительности CCD до сих пор являются пока недостижимым ориентиром для CMOS, поэтому они все еще широко
используются за исключением мегапиксельных вариантов, которые очень дорого стоят и применяются в основном для специальных задач.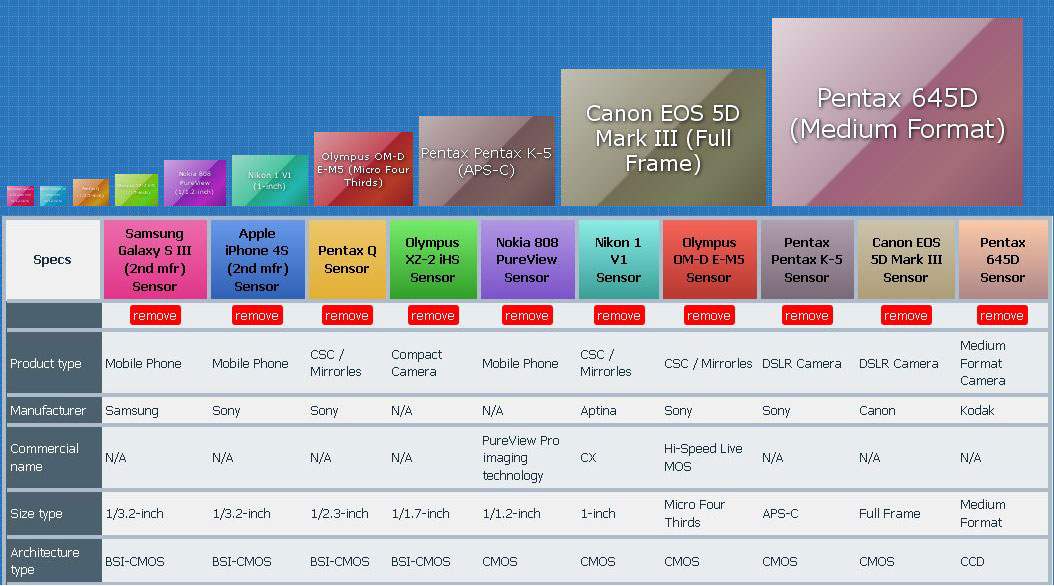
CMOS: достоинства и недостатки
Сенсоры CMOS были изобретены в конце 1970-х гг., но их производство удалось начать только в 1990-е по причине технологических проблем. И сразу наметились их основные достоинства и недостатки, которые и сейчас остаются актуальными.
К достоинствам можно отнести большую интеграцию и экономичность сенсора, более широкий динамический диапазон, простоту производства и меньшую стоимость, особенно мегапиксельных вариантов.
С другой стороны, CMOS-сенсоры обладают меньшей чувствительностью, обусловленной, при прочих равных условиях, большими потерями в фильтрах структуры RGB, меньшей полезной площадью светочувствительного элемента. В результате множества переходных элементов, включая усилители в тракте каждого пикселя, обеспечить равномерность параметров всех чувствительных элементов значительно сложнее в сравнении с CCD. Но совершенствование технологий позволило приблизить чувствительность CMOS к лучшим образцам CCD, особенно в мегапиксельных вариантах.
Ранние сторонники CMOS утверждали, что эти структуры будут гораздо дешевле, потому что могут быть произведены на том же оборудовании и по тем же технологиям, что и микросхемы памяти и логики. Во многом данное предположение подтвердилось, но не полностью, поскольку совершенствование технологии привело к практически идентичному по сложности производственному процессу, как и для CCD.
С расширением круга потребителей за рамки стандартного телевидения разрешение матриц стало непрерывно расти. Это бытовые видеокамеры, электронные фотоаппараты и камеры, встроенные в средства коммуникации. Кстати, для мобильных устройств вопрос экономичности довольно важный, и здесь у CMOS-сенсора нет конкурентов. Например, с середины 1990-х гг. разрешение матриц ежегодно вырастало на 1–2 млн элементов и теперь достигает 10–12 Мпкс. Причем спрос на CMOS-сенсоры стал доминирующим и сегодня превышает 100 млн единиц.
CMOS: улучшение чувствительности
Первые образцы камер наблюдения конца 1990-х – начала 2000-х с CMOS-матрицами имели разрешение 352х288 пкс и чувствительность даже для черно-белого варианта около 1 лк. Цветные варианты уже стандартного разрешения отличались чувствительностью около 7–10 лк.
Цветные варианты уже стандартного разрешения отличались чувствительностью около 7–10 лк.
Что предлагают поставщики
В настоящее время чувствительность CMOS-матриц, безусловно, выросла, но не превышает для типовых вариантов цветного изображения величины порядка нескольких люксов при разумных величинах F числа объектива (1,2– 1,4). Это подтверждают данные технических характеристик брендов IP-видеонаблюдения, в которых применяются CMOS-матрицы с прогрессивной разверткой. Те производители, которые заявляют чувствительность около десятых долей люкса, обычно уточняют, что это данные для меньшей частоты кадров, режима накопления или по крайней мере включенной и достаточно глубокой АРУ (AGC). Причем у некоторых производителей IP-камер максимальная АРУ достигает умопомрачительной величины –120 дБ (1 млн раз). Можно надеяться, что чувствительность для этого случая в представлении производителей предполагает пристойное отношение «сигнал/шум», позволяющее наблюдать не один только «снег» на экране.
Инновации улучшают качество видео
В стремлении улучшить характеристики CMOS-матриц компания Sony предложила ряд новых технологий, обеспечивающих практическое сравнение CMOS-матриц с CCD по чувствительности, отношению «сигнал/шум» в мегапиксельных вариантах.
Новая технология производства матриц Exmor основана на изменении направления падения светового потока на матрицу. В типовой архитектуре свет падает на фронтальную поверхность кремниевой пластины через и мимо проводников схемы матрицы. Свет рассеивается и перекрывается этими элементами. В новой модификации свет поступает на тыльную сторону кремниевой пластины. Это привело к существенному росту чувствительности и снижению шума CMOS-матрицы. На рис. 5 поясняется различие структур типовой матрицы и матрицы Exmor, показанных в разрезе.
На фото 1 приведены изображения тестового
объекта, полученные при освещенности 100 лк (F4.0 и 1/30 с) камерой с CCD (фронтальное освещение) и CMOS Exmor, имеющих одинаковый формат и разрешение 10 Мпкс.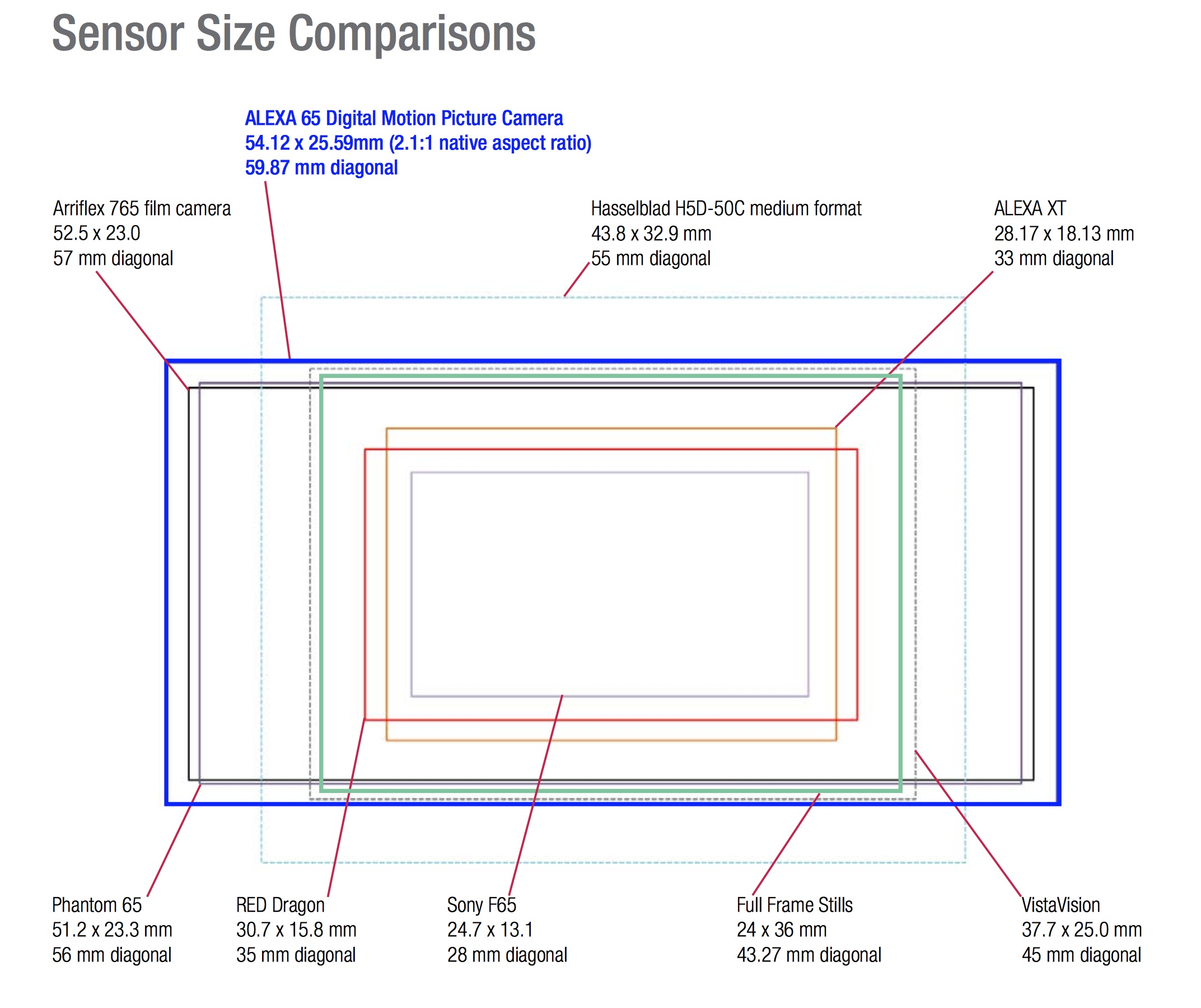 Очевидно, что изображение камеры с CMOS по крайней мере не хуже изображения с CCD.
Очевидно, что изображение камеры с CMOS по крайней мере не хуже изображения с CCD.
Другим способом улучшения чувствительности CMOS-сенсоров является отказ от прямоугольного расположения пикселей с построчным сдвигом красного и синего элементов. При этом в построении одного элемента разрешения используются по два зеленых пикселя – синий и красный из разных строк. Взамен предлагается диагональное расположение элементов с использованием шести соседних зеленых элементов для построения одного элемента разрешения. Такая технология получила название ClearVid CMOS. Для обработки предполагается более мощный сигнальный процессор изображений. Различие структур расположения цветных элементов иллюстрируются рис. 6.
Считывание информации осуществляется быстродействующим параллельным аналого-цифровым преобразователем. При этом частота кадров прогрессивной развертки может достигать 180 и даже 240 кадр/с. При параллельном съеме информации устраняется диагональный сдвиг кадра, привычный для CMOS-камер с последовательным экспонированием и считыванием сигнала, так называемый эффект Rolling Shutter – когда полностью отсутствует характерный смаз быстро движущихся объектов.
На фото 2 приведены изображения вращающегося вентилятора, полученные CMOS-камерой с частотой кадров 45 и 180 кадр/с.
Полноценная конкуренция
В качестве примеров мы приводили технологии Sony. Естественно, CMOS-матрицы, как и CCD, производят и другие компании, хотя не в таких масштабах и не столь известные. В любом случае все так или иначе идут примерно одним путем и используют похожие технические решения.
В частности, известная технология матриц Panasonic Live-MOS также существенно улучшает характеристики CMOS-матриц и, естественно, похожими методами. В матрицах Panasonic уменьшено расстояние от фотодиода до микролинзы. Упрощена передача сигналов с поверхности фотодиода. Уменьшено количество управляющих сигналов с 3 (стандартные CMOS) до 2 (как в CCD), что увеличило фоточувствительную область пикселя. Применен малошумящий усилитель фотодиода. Используется более тонкая структура слоя датчиков. Сниженное напряжение питания уменьшает шум и нагрев матрицы.
Можно констатировать, что мегапиксельные матрицы CMOS уже могут успешно конкурировать с CCD не только по цене, но и по таким проблемным для этой технологии характеристикам, как чувствительность и уровень шума. Однако в традиционном CCTV телевизионных форматов CCD-матрицы остаются пока вне конкуренции.
Опубликовано: Журнал «Системы безопасности» #5, 2011
Посещений: 92566
Автор
| |||
В рубрику «Видеонаблюдение (CCTV)» | К списку рубрик | К списку авторов | К списку публикаций
Матрицы фотоаппаратов Nikon
© 2017 Vasili-photo. com
com
В приведённой ниже таблице собраны некоторые сведения о матрицах, использующихся в цифровых зеркальных фотоаппаратах Nikon.
Каждая строка таблицы соответствует определённой матрице. Для каждой матрицы указаны производитель и модель (за исключением тех случаев, когда модель неизвестна). Далее перечислены фотоаппараты Nikon, в которых данный сенсор когда-либо использовался (камеры, выпускающиеся в настоящее время, выделены жирным шрифтом). Затем указан период, на протяжении которого матрица (точнее, оснащаемые ей камеры) находилась (или находится) в производстве, тип матрицы, её формат, число мегапикселей и общий рейтинг качества изображения по данным DxOMark.
| Производитель и модель матрицы | Камеры | Годы выпуска | Тип матрицы | Формат | Мп | Рейтинг DxOMark |
| Sony IMX309AQJ | D850 | с 2017 | КМОП | FX | 45,4 | 100 |
| Sony IMX321 | D500, D7500 | с 2016 | КМОП | DX | 20,9 | 84-86 |
| Sony T4K54 | D5 | с 2016 | КМОП | FX | 20,8 | 88 |
| Sony IMX193AQK | D5300, D3300, D5500, D3400, D5600 | с 2013 | КМОП | DX | 24,2 | 82-86 |
| Toshiba HEZ1 TOS-5105 | D5200, D7100, D7200 | 2012-2017 | КМОП | DX | 24,2 | 83-87 |
| Sony IMX128AQP | D600, D610, D750 | с 2012 | КМОП | FX | 24,3 | 93-94 |
| Nikon NC81369R | D3200 | 2012-2014 | КМОП | DX | 24,2 | 81 |
| Sony IMX094AQP | D800, D810 | 2012-2017 | КМОП | FX | 36,3 | 95-97 |
| Nikon NC81366W | D4, D4s, Df | с 2012 | КМОП | FX | 16,2 | 89 |
| Sony IMX071 | D7000, D5100 | 2010-2013 | КМОП | DX | 16,2 | 80 |
| Nikon NC81362A | D3100 | 2010-2012 | КМОП | DX | 14,2 | 67 |
| Nikon NC81361A | D3s | 2009-2011 | КМОП | FX | 12,1 | 82 |
| Sony IMX028 (?) | D3X | 2008-2012 | КМОП | FX | 24,5 | 88 |
| Sony IMX038BQL | D90, D5000, D300s | 2008-2014 | КМОП | DX | 12,3 | 70-73 |
| Sony IMX038BQL | D300 | 2007-2009 | КМОП | DX | 12,3 | 67 |
| Nikon NC81338L | D3, D700 | 2007-2012 | КМОП | FX | 12,1 | 81 |
| Sony ICX493AQA | D80, D40x, D60, D3000 | 2006-2010 | ПЗС | DX | 10,2 | 61-65 |
| Sony ICX483AQA | D200 | 2005-2007 | ПЗС | DX | 10,2 | 64 |
| Sony IMX007AQ | D2X, D2Xs | 2004-2008 | КМОП | DX | 12,2 | 59 |
| Sony ICX453AK | D70, D70s, D50, D40 | 2004-2009 | ПЗС | DX | 6,1 | 50-56 |
| Nikon JFET-LBCAST | D2H, D2Нs | 2003-2007 | LBCAST | DX | 4,1 | 40 |
| Sony ICX413AQ | D100 | 2002-2005 | ПЗС | DX | 6,1 | — |
| Sony | D1X | 2001-2004 | ПЗС | DX | 5,3 | — |
| Sony | D1, D1H | 1999-2003 | ПЗС | DX | 2,7 | — |
Очевидно, что основным поставщиком сенсоров для фотоаппаратов Nikon является компания Sony, однако время от времени Nikon использует матрицы собственного производства. Впрочем, некоторые матрицы Nikon (NC81338L, NC81361A, NC81362A, NC81366W и NC81369R) были лишь спроектированы инженерами Nikon, а их непосредственным производством занималась компания Renesas.
Впрочем, некоторые матрицы Nikon (NC81338L, NC81361A, NC81362A, NC81366W и NC81369R) были лишь спроектированы инженерами Nikon, а их непосредственным производством занималась компания Renesas.
В фотокамерах D5200, D7100, D7200 установлен сенсор Toshiba. В 2015 году Sony скупила заводы Toshiba, занимающиеся производством фотоматриц, и потому в качестве производителя матрицы T4K54, используемой в фотоаппарате Nikon D5, указан нынешний владелец завода, на котором она выпускается, т.е. Sony, несмотря на то, что раньше этот завод принадлежал Toshiba.
Мне неизвестны модели сенсоров, использовавшихся в первых цифровых зеркальных фотоаппаратах Nikon – D1, D1H и D1X. Кроме того, я не вполне уверен: точно ли в Nikon D3X устанавливалась та же самая матрица Sony IMX028, что и в Sony α900.
Для некоторых сенсоров общий рейтинг матрицы DxOMark указан в виде диапазона. Это связано с тем, что качество изображения зависит не только от самой матрицы, но и от сопутствующей ей электроники (АЦП, процессор и пр. ), а также от алгоритмов первичного шумоподавления и оцифровки сигнала. Вследствие этого у разных фотокамер, оснащённых одним и тем же сенсором, качество изображения может незначительно различаться. Например, общий рейтинг DxOMark для Nikon D810 составляет 97 баллов, а для Sony A7R – 95 баллов, хотя матрица в обеих камерах одна и та же – Sony IMX094AQP. Иными словами, Nikon ухитряется добиваться от сенсоров Sony большей производительности, чем это получается у самой Sony.
), а также от алгоритмов первичного шумоподавления и оцифровки сигнала. Вследствие этого у разных фотокамер, оснащённых одним и тем же сенсором, качество изображения может незначительно различаться. Например, общий рейтинг DxOMark для Nikon D810 составляет 97 баллов, а для Sony A7R – 95 баллов, хотя матрица в обеих камерах одна и та же – Sony IMX094AQP. Иными словами, Nikon ухитряется добиваться от сенсоров Sony большей производительности, чем это получается у самой Sony.
Спасибо за внимание!
Василий А.
Post scriptum
Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.
Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.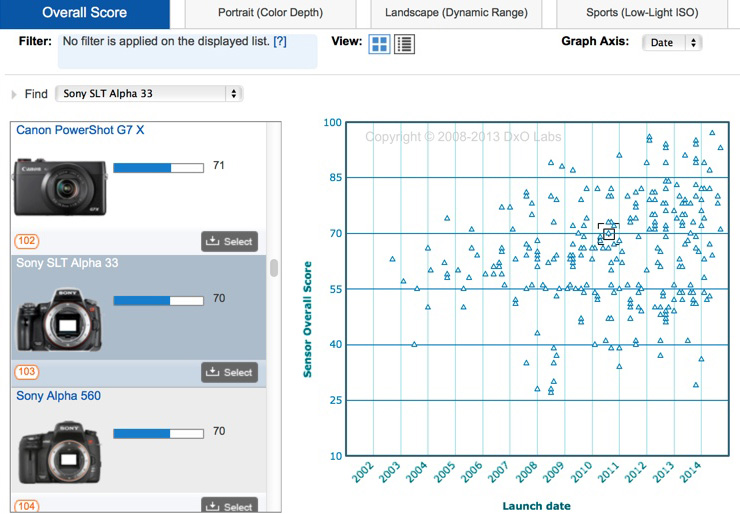
Желаю удачи!
Дата публикации: 14.01.2016 |
Вернуться к разделу «Фотооборудование»
Перейти к полному списку статей
Антимаркетинг: сравниваем камеры популярных смартфонов
Производители смартфонов прибегают к разным трюкам, показывая возможности встроенных камер и «забывая» сказать, почему вы вряд ли получите аналогичный результат. Мы попробуем подкинуть пищу для размышлений и помочь вам противостоять такой недобросовестной рекламе.
Методика тестирования
В этой статье сравниваются самые ходовые модели 2018 – 2019 года выпуска из среднего ценового сегмента. Формально в него же попадают и подешевевшие флагманы прошлых лет, но давайте ограничимся смартфонами одного исходного класса.
За снимками обратимся к специалистам из GSMArena. Они тестируют камеры смартфонов с 2010 года и накопили очень внушительную базу. Обычному покупателю будет сложно понять результат из тестовых таблиц, поэтому мы сделаем необходимые пояснения.
В сравнении принимают участие только основные (тыловые) камеры, работающие в автоматическом режиме при съёмке одиночных кадров цветных постеров и специальной тестовой карточки – фотографической миры PIMA/ISO 12233.
На всех смартфонах отключены бьюти-фильтры, искусственный недоинтеллект и прочие улучшалки, а где это возможно – установлен стиль изображения «точное». Смартфоны установлены на штатив. Делается серия кадров, из которой вручную выбирается самое резкое изображение. Для полноты картины съёмка повторяется в условиях нормальной и низкой освещённости. Значения ISO и выдержки, а также баланс белого устанавливаются камерами автоматически.
Матрицы и фокусные расстояния у всех разные, поэтому размер изображения тоже будет отличаться. Мы приводим идентичные фрагменты исходных кадров в формате PNG безо всякого масштабирования.
Мы приводим идентичные фрагменты исходных кадров в формате PNG безо всякого масштабирования.
Оптическое разрешение
Если говорить о макро-режиме при ярком освещении, то здесь на разрешение больше всего влияет объектив. У всех смартфонов среднего уровня оптика одного класса, поэтому оно примерно одинаковое и находится в районе 12 – 16 линий на миллиметр. Вот как это выглядит на оказавшейся под рукой координатной сетке для цифровых микроскопов (100% кроп без обработки с 12 МП матрицы при ISO 100, съёмка со штатива).
Координатная сетка с шагом 0,1 мм (кликните, чтобы открыть на отдельной вкладке).
Между рисками миллиметровой шкалы есть ещё девять тонких линий (цена деления 0,1 мм), и они чётко видны. 20 и более линий на миллиметр (lpmm) смартфон уже не покажет – они просто визуально сольются.
При обычной съёмке (с расстояния 40 см и более) широкоугольный объектив смартфона не способен передать мелкие детали из-за их малого углового размера. На общее восприятие картинки в большей степени влияет уже матрица, а она в любом смартфоне оставляет желать лучшего из-за очень низкого соотношения сигнал/шум. Алгоритмы шумоподавления всегда скрадывают детализацию. Теряется текстура, а эффективное разрешение падает до пары линий на миллиметр.
Алгоритмы шумоподавления всегда скрадывают детализацию. Теряется текстура, а эффективное разрешение падает до пары линий на миллиметр.
Вообще измерение оптического разрешения камеры – довольно сложная и дорогая задача. Мы возьмём профессиональные таблицы, но не будем вас мучить математикой. Просто скажем, что коэффициент пересчёта в lpmm для них составляет 0,075. То есть, если вы видите отдельные линии до маркера «20», а на промежуточной отметке «22» они уже слились, значит – разрешение составит полторы линии на миллиметр.
Насколько это много? Такая характеристика типична для цифромыльниц, которые сегодня вытеснили смартфоны. Системные камеры и зеркалки любительского уровня со съёмным объективом в комплекте обычно дают 20-30 lpmm (в самой резкой зоне по центру), а профессиональные – до 100 lpmm, но разглядеть это великолепие можно только при использовании полнокадровых и среднеформатных матриц. В смартфоне такие просто негде разместить.
Сравнение физических размеров матриц у смартфонов и разной фототехники (картинка кликабельна).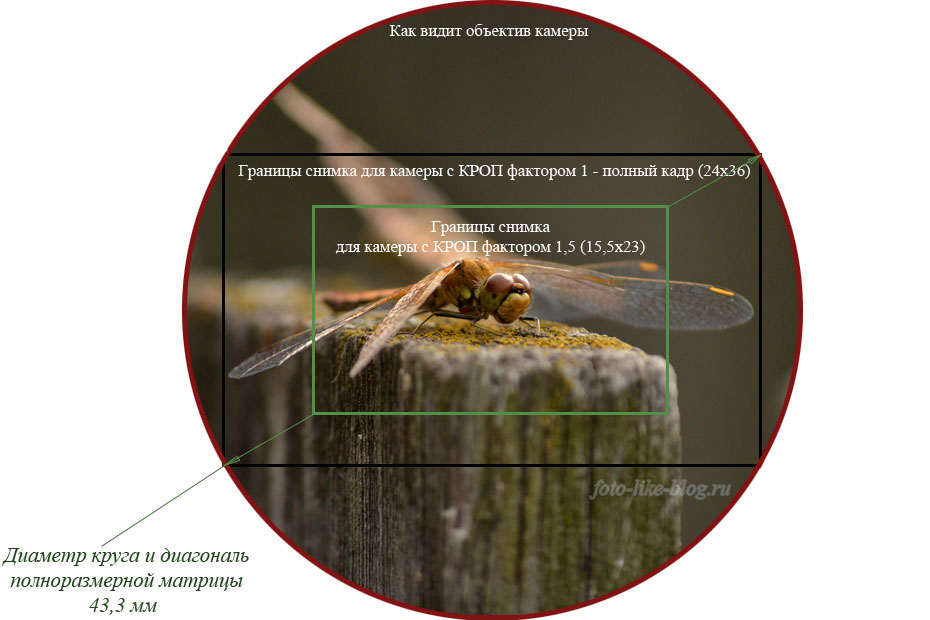
Оценка результатов
В верхнем ряду каждого снимка представлена пара фрагментов миры. Смотрим, где линии впервые видны по-отдельности. Настолько чётко, что их легко сосчитать. Чем левее (больше значение в подписи), тем выше реальная разрешающая способность камеры. Для наглядного сравнения относительных результатов этого достаточно, а определение точных частотно-контрастных характеристик оставим лабораториям, специализирующимся на оптике.
Второй ряд демонстрирует цветную вышивку на сером фоне. Он хорошо показывает степень детализации изображения и характер его огрубления при съёмке в полутьме.
Третий ряд показывает точность автофокуса на цветном фоне и качество цветопередачи в разных условиях освещения. Некоторые смартфоны искусственно усиливают яркость и/или насыщенность отдельных оттенков, делая цвета неестественными.
Huawei P Smart (2019)
Характеристики камеры: 13 MP, f/1.8, PDAF (подробнее см. раздел «Краткий словарь терминов»).
раздел «Краткий словарь терминов»).
(кликните для увеличения)
У Huawei P Smart (2019) камера «мылит» вплоть до отметки «24». Действительно отдельными линии начинают восприниматься с промежуточного маркера 22 и далее (подробнее см. раздел «Оптическое разрешение»). Точнее трудно сказать из-за того, что изображение слегка не в фокусе (напомню, что это лучшая попытка в серии). Автофокус у P Smart явно оставляет желать лучшего.
Правый верхний угол снимка показывает диапазон яркости камеры. На нём видны провалы в тенях. Полутона после отметки 15 сливаются в сплошной чёрный. Впрочем, это совершенно типичный результат для смартфонов. Немного расширить диапазон яркости поможет съёмка в HDR (только статичных объектов со штатива) или в RAW (хотя у смартфонов это повышает разрядность каждого канала всего до 10-12 бит, а не до 14 бит, как у зеркалок).
Пара изображений посередине демонстрирует детализацию при минимальном ISO (слабое или выключенное шумоподавление) и высоком ISO (сильное шумоподавление). На левой картинке текстура вышивки сильно смазана (отчасти это объясняется и небольшой промашкой автофокуса), а на правой сглаживание затронуло даже крупные стежки. Также ожидаемо видим ухудшение цветопередачи – серые вертикальные линии теперь выглядят зелёными (цвета окружающего их фона).
На левой картинке текстура вышивки сильно смазана (отчасти это объясняется и небольшой промашкой автофокуса), а на правой сглаживание затронуло даже крупные стежки. Также ожидаемо видим ухудшение цветопередачи – серые вертикальные линии теперь выглядят зелёными (цвета окружающего их фона).
Вообще с цветопередачей тёмных полутонов у Huawei P Smart (2019) дела обстоят неважно, особенно на высоких значениях ISO. Это видно и на картинке с цветными карандашами, где тёмно-зелёный и тёмно-синий грифель на ISO 64 ещё хоть как-то различимы, а при ISO 800 уже выглядят практически одинаково чёрными. Баланс белого также далёк от идеального. Серый фон миры в левом верхнем углу имеет зеленоватый оттенок.
Huawei P20 Lite
Камера: 16 MP, f/2.2, PDAF
(кликните для увеличения)
У P20 lite лучше сработал автофокус (изображение более резкое), однако из-за мелких пикселей (1,0 мкм) видим сильные цветовые шумы. В результате их подавления итоговое разрешение снимка даже чуть ниже, чем у P Smart – до маркера «20» линии сливаются.
На высоких ISO ослик выглядит бледным и зернистым даже в районе гладкой серой вставки. Кстати, ISO пришлось поднимать до 1000 единиц – сказывается сравнительно низкая светосила объектива.
Зато баланс белого очень хорош, а вертикальные полоски седла в полутьме сохранили настоящий серый цвет – огрубление цветопередачи у P20 Lite не такое сильное. При хорошей освещённости картинка и вовсе радует – угадываются средние по размеру стежки, а на карандашах можно разглядеть текстуру.
Huawei Mate 20 lite
Камера: 20 MP, f/1.8, PDAF.
(кликните для увеличения)
Число мегапикселей растёт, а эффективная разрешающая способность в лучшем случае остаётся такой же. При ярком освещении все изображения выглядят презентабельно. Цвета не вызывают каких-то сомнений, хотя баланс белого слегка смещён в область более низкой цветовой температуры (серый выглядит желтоватым).
При слабом освещении автофокус промахнулся – вышивка получилась очень смазанной и бледной. Цвета поплыли: серый фон порозовел, а тёмно-зелёный стал более синим (бирюзовым). От текстуры дерева не осталось и следа. В полутьме таким смартфоном даже не стоит пытаться фотографировать.
Цвета поплыли: серый фон порозовел, а тёмно-зелёный стал более синим (бирюзовым). От текстуры дерева не осталось и следа. В полутьме таким смартфоном даже не стоит пытаться фотографировать.
Honor 8X
Камера: 20 MP, f/1.8, PDAF
(кликните для увеличения)
Казалось бы, имеем те же 20 мегапикселей при диафрагме 1.8 и то же разрешение, но в итоге получаем немного другой результат. Баланс белого смещён в противоположную сторону: занижен синий канал и слегка завышен зелёный. Провалы в тенях чуть глубже – уже с маркера «13» всё сливается в чёрный. Зато автофокус точнее сработал, из-за чего вышивка выглядит детальнее – очень чёткие края. На высоких ISO изображение такое же замыленное, а серые стежки на зелёном фоне опять стали зелёными.
Honor 10 Lite
Камера: 13 MP, f/1.8, PDAF.
(кликните для увеличения)
Облегчённая версия десятого «Хонора» вытягивает разрешение до отметки «24» и даже чуть больше, но тёмные полутона сливаются как у всех. Баланс белого слегка смещён в сторону тёплых оттенков. Сами цвета выглядят естественно. Детализация средняя при хорошем освещении. Съёмка в темноте чуть лучше по сравнению с 8X – текстуры сглаживаются, но не пропадают. Тонкие серые полосы также стали зелёными, края объектов заметно размыты из-за сильного шумоподавления.
Баланс белого слегка смещён в сторону тёплых оттенков. Сами цвета выглядят естественно. Детализация средняя при хорошем освещении. Съёмка в темноте чуть лучше по сравнению с 8X – текстуры сглаживаются, но не пропадают. Тонкие серые полосы также стали зелёными, края объектов заметно размыты из-за сильного шумоподавления.
Motorola (Lenovo) Moto G6
Камера: 12 MP, f/1.8, PDAF.
(кликните для увеличения)
Отдельные линии видны от промежуточного маркера 22. При 12 Мп эффективное разрешение снимков почти такое же, как у Huawei Mate 20 lite с его 20 Мп сенсором. Сказывается увеличенный размер пикселей (1,4 мкм), дающий сравнительно низкие шумы.
Баланс белого плывёт в сторону низкой цветовой температуры (слегка желтит). Провалы в тенях довольно глубокие (столбики градиентной заливки 14 – 19 сливаются). Текстура карандашей немного смазана, цвета естественные.
При ярком освещении вышивка выглядит очень детально: видно даже мелкие стежки. Это один из самых резких кадров в обзоре. На высоких ISO автофокус наводится точнее, чем у большинства смартфонов, но сглаживание и огрубление цветопередачи при этом сильнее заметны.
Nokia 7.1
Камера: 12 MP, f/1.8, Dual Pixel PDAF
(кликните для увеличения)
Главное отличие – технология улучшенного фазового автофокуса. Как плоские, таки и объёмные предметы на всех снимках очень чёткие. Эффективное разрешение аналогично Moto G6 – линии сливаются в районе маркера «22».
Алгоритм подавления яркостных шумов здесь менее агрессивный, поэтому сравнительно высокая детализация сохраняется даже на высоких значениях ISO. Цвета почти не бледнеют и слабо искажаются – серые полоски на зелёном фоне остаются серыми.
Samsung Galaxy A7 (2018)
Камера: 24 МP, f/1.7, PDAF
(кликните для увеличения)
Работу автофокуса трудно назвать образцовой – фотографии карандашей смазаны даже при съёмке в условиях яркого освещения. Оптическое разрешение камеры весьма радует: отдельные линии видны вплоть до маркера «28», хроматических аберраций невооружённым глазом не наблюдается.
Очень заметна светосильная оптика: в то время как другие смартфоны поднимают ISO до 800 – 1000 единиц, A7 в тех же условиях достаточно 400. Как результат – меньше яркостных шумов и чище картинка.
Однако алгоритмы цветового шумоподавления зачем-то сделали очень агрессивными – текстура карандашей пропала полностью даже при ISO50, вместо рисунка дерева видно только мутные пятна. Мелкие стежки на вышивке превратились в группу артефактов. Вот так на уровне софта можно угробить хорошую аппаратную платформу.
Xiaomi RedMi Note 7
Камера: 48 MP, f/1.8, PDAF
(кликните для увеличения)
С яркостным диапазоном у этой камеры всё как обычно, поэтому мы пропустим 50 оттенков серого, чтобы показать иллюзию 48 мегапикселей за счёт технологии Quad Bayer Array. Здесь её работа отчётливо видна в верхнем ряду.
Повышение количества пикселей матрицы в четыре раза никак не влияет на реальное оптическое разрешение: на обоих снимках линии сливаются за маркером 22. Более того, на них очень заметны хроматические аберрации – это кривая работа алгоритма интерполяции «тетрапикселей» (см. Краткий словарь терминов) на этапе дематризации.
Автофокус не смог точно навестись на резкость, поэтому даже при хорошем освещении мелкие детали смазываются. Текстура карандашей выглядит как артефакты пикселизации. С таким же успехом вы можете растянуть вчетверо картинку, снятую на Honor 8X, Moto G6 или Nokia 7.1.
Xiaomi Mi8 Lite
Камера: 12 МP, f/1.9, Dual Pixel PDAF
(кликните для увеличения)
Оптическое разрешение чуть выше среднего для группы прямых конкурентов – линии сливаются за маркером «22». Диапазон яркости максимальный для восьмибитной растровой картинки – различимы все градиентные столбики до маркера 16 (B) включительно.
Радуют щадящие алгоритмы шумоподавления. На всех снимках хорошо видна текстура и мелкие детали. Их можно разглядеть даже на ISO 800, что большая редкость.
Баланс белого смещён в сторону жёлто-зелёного оттенка. Автофокус Dual Pixel PDAF работает менее точно, чем аналогичный у Nokia 7.1.
Краткий словарь терминов
PDAF – Phase Detection Auto Focus, фазовый автофокус. Для проверки автоматической фокусировки в нём определяется схождение лучей из нескольких точек с центра и краёв объектива. В «зеркалках» он работает шустро и довольно точно, а в телефонах – гораздо хуже из-за габаритных ограничений. В темноте часто промахивается, так как часть лучей просто не фиксируется и проверить их сходимость не удаётся.
Dual Pixel PDAF – улучшенный фазовый автофокус, в котором для оценки резкости используется почти вся площадь матрицы. Гораздо быстрее и точнее PDAF. Разница особенно заметна при низкой освещённости.
Laser AF – лазерный автофокус. Работает как лазерный дальномер. Объект съёмки подсвечивается ИК-лазером, после чего оценивается время получения отражённого от него света. По этим данным вычисляется расстояние до объекта, а блок линз быстро перемещается на заранее заданную величину. В целом работает быстрее PDAF и даёт меньше ошибок (особенно в темноте), но из-за низкой мощности лазера его заявленная дальность ограничена пятью метрами, а реально эффективная – двумя-тремя.
f/x.y – диафрагменное число, или просто диафрагма. Показывает светопропускание объектива через отношение входного зрачка объектива (принимается за единицу) к заднему фокусному расстоянию. У смартфонов регулируемой диафрагмы нет, поэтому f принимается соответствующим её максимально открытому положению. Условно говоря, чем меньше знаменатель – тем лучше. Например, камера с f/1.8 пропускает за единицу времени больше света (обладает большей светосилой), чем с f/2.2. В одинаковых условиях первая будет снимать на более коротких выдержках и/или устанавливать меньшее значение ISO, что положительно скажется на качестве снимка.
ISO – светочувствительность матрицы, оцениваемая по стандарту ISO 12232:2006. Чем выше ISO, тем при более низкой освещённости можно снимать, но достигается это ценой повышения яркостных шумов. На ISO 50 – 200 эти шумы незначительны и картинка выглядит максимально чёткой. На ISO 800 и выше включаются алгоритмы агрессивного шумоподавления, из-за чего изображение становится блёклым и сильно сглаженным. Мелкие детали теряются полностью, цветопередача огрубляется.
1/x.y» – эквивалентный размер матрицы. Чем меньше число в знаменателе, тем крупнее матрица (см таблицу в начале статьи). Сами пиксели (при одинаковом разрешении) тоже крупнее, поэтому ниже уровень цветовых шумов. Проще говоря, в пределах одного поколения матрица 1/1.7″ даёт более детальное изображение, чем 1/2.7″.
X мм – фокусное расстояние в эквиваленте кадра 35-мм плёнки. Чем меньше это значение, тем более широкий угол обзора у камеры. Больше объектов влезает в кадр ценой усиления геометрических искажений.
MP – разрешение матрицы в мегапикселях (миллионах точек). Правило «чем больше, тем лучше» здесь работает только до определённого предела – пока размер пикселей не станет слишком мелким. Сейчас у лучших матриц для смартфонов пиксели от 1,2 мкм и более, но обратите внимание: 1,6 мкм обычно указывается как маркетинговый ход. У современных матриц 40 MP эквивалентны десяти «тетрапикселям» – квадрату из четырёх пикселей под общим светофильтром одного цвета (технология Quad Bayer Array). Здесь 1,6 мкм – сторона квадрата. Нетрудно подсчитать, что размер одного пикселя составляет 0,8 мкм.
Выводы
В нашем кратком сравнении участвовали десять смартфонов с матрицами от 12 до 48 Мп. С лёгкой руки маркетологов большинство покупателей считают, что чем больше мегапикселей, тем лучше изображение. Возможно, это и было так на заре цифровой фотографии (разница между 0,3 и 3 Мп действительно не вызывает сомнений), но сейчас дальнейшая гонка за разрешением КМОП-сенсора у смартфонов потеряла смысл. Картинка просто становится крупнее, а вот будет ли она детальнее – зависит совершенно от других факторов. Главные из них – свойства оптической системы, физические размеры матрицы и алгоритмы обработки.
Каждый элемент объектива вносит свои оптические аберрации, а процессор обработки изображений ещё сильнее искажает картинку, пытаясь подавить цифровой шум. Особенно это заметно на крошечных матрицах смартфонов. В какой-то момент достигается предел разрешающей способности системы, и вы больше не увидите новых деталей, как бы сильно ни увеличивали фотографию. Первые «зеркалки» с матрицами 3 – 5 Мп и нормальным объективом до сих пор снимают лучше любого смартфона, будь в нём хоть 48 миллионов подслеповатых наноглаз.
Гораздо большее значение для смартфона имеет система автофокуса, светосила и настройка программных алгоритмов шумоподавления. Большинство кадров снимаются с рук, поэтому оптическая стабилизация очень выручит. Если же её нет, или она формальная – добавьте света (это укоротит выдержку и/или ISO, сделав снимок чётче и чище), либо воспользуйтесь штативом.
Баланс белого не совсем корректно определяется всеми смартфонами даже в идеальных условиях съёмки, поэтому по возможности снимайте в RAW. Тогда при постобработке вы просто укажите нужную цветовую температуру, и все полутона автоматически исправятся без потерь. Также этот формат позволит вам немного увеличить диапазон яркости и скорректировать свет/тень без появления заметных артефактов.
Какая матрица для фотоаппарата лучше: как выбрать
Покупая фотоаппарат, неважно какой: профессионального класса или рядовой бюджетный компакт для съемок друзей и семьи на природе, хочется, чтобы снимки получались качественными, а сам аппарат давал как можно больше свободы. Зная, какая матрица для фотоаппарата лучше, можно не впадать в ступор в магазине при виде двух моделей разных марок, которые выглядят одинаково, но стоят очень по-разному. Все дело в сенсоре, который и отвечает за то, какое изображение будет получаться и насколько гибкие рамки пользования фотоаппаратом будут у владельца.
Немного технических сведений
Матрицы цифровых фотоаппаратов делятся на два основных типа по применяемым полупроводникам и технологии считывания информации.
- Тип матрицы ПЗС (CCD) – самый распространенный. Это достаточно дешевая технология, информация об изображении считывается последовательно с каждой ячейки.
- КМОП матрицы CMOS дороже, но эффективнее в плане скорости работы, поскольку позволяют считывать данные сразу со всех светочувствительных элементов. Такие сенсоры устанавливаются в дорогих камерах, поскольку ни один производитель не пройдет мимо шанса предоставить пользователю возможности съемки с очень малыми выдержками, что в свою очередь усложняет аппаратно-программный комплекс.
Большинство фотоаппаратов пользовательского класса оснащено ПЗС матрицами. При этом ставится вполне ожидаемое условие: для получения действительно качественных снимков при естественном освещении (или при недостаточном) лучше использовать штатив, поскольку время выдержки будет значительным. Аналогично – не получится делать снимки крайне быстро, поскольку нужно время на получение и обработку изображения.
Некоторые производители решают последнюю проблему достаточно просто: оснащают фотоаппараты буфером памяти. Туда помещаются кадры до обработки, когда ведется съемка в так называемом спортивном режиме – серией за короткий промежуток времени.
Дорогие фотокамеры, оснащенные КМОП матрицами, позволяют делать снимки “с рук” с малой выдержкой, имеют высокую светочувствительность и низкий уровень шума. С помощью такого оборудования можно проводить экспонометрию, снижается время автофокусировки, естественно, легко сделать хороший кадр.
Еще одна технология, которая применяется в самой дорогой фототехнике – многослойные матрицы. Это не очередной пункт в списке «виды матриц». Светочувствительная зона таких аппаратов состоит из трех слоев ПЗС, каждый из которых считывает только один цвет. В результате качество изображения просто потрясает. Техника с данной технологией особо маркируется: 3CCD.
Последнее, что стоит упомянуть, – технологические размеры матриц. ПЗС сенсоры можно сделать маленькими, они построены на кремниевых элементах. А КМОП матрицы достаточно большие, что является еще одним рациональным доводом в пользу их применения в дорогой профессиональной технике.
Количественный показатель качества
Задавая себе вопрос, какая матрица фотоаппарата лучше,- можно достаточно быстро получить ответ без необходимости вникать в технологические особенности. Обратите внимание на следующие характеристики:
- заявленное количество мегапикселей в характеристике камеры;
- эффективное количество пикселей, которое ответственные производители указывают в документации к фотоаппарату;
- возможные размеры изображений, которые можно делать с помощью камеры.
Производители дешевых моделей фотоаппаратов часто лукавят, указывая, прежде всего, размерность картинки и выставляя огромные цифры как эффективный рекламный ход. Это не говорит о качестве получаемых снимков. Типы матриц фотоаппаратов могут быть разного класса. Однако если сенсор не имеет достаточной разрешающей способности, большие изображения на выходе будут иметь низкую детализацию и высокий уровень шума.
Еще больше о качестве камеры скажет соотношение между заявленными мегапикселями матрицы и количеством эффективных точек. Это напрямую говорит о применяемой оптике. Если аппаратная часть выполнена ответственно, заявленное и эффективное количество пикселей будет почти одинаково, что не только положительно характеризует продажную цену, но и напрямую отвечает за качество снимков.
Светочувствительность и шумы
Светочувствительность матрицы – еще одна характеристика, которая описывает фотоаппарат. Покупать камеру стоит, ориентируясь на планируемые возможности применения. Сегодня в документации в графе светочувствительности можно встретить очень высокие цифры – до 51000 и больше. Однако это не говорит напрямую о возможности делать качественные снимки. Нет и рекомендаций, какой должна быть светочувствительность. Работает все следующим образом:
- для получения хорошего изображения требуется обеспечить выдержку, время которой зависит от уровня освещенности и светочувствительности матрицы;
- при среднем и низком освещении приходится применять штатив;
- если хочется продолжать снимать “с рук”, можно программно поменять уровень светочувствительности матрицы в настройках фотоаппарата.
Однако высокая светочувствительность при малой установленной выдержке – это прямой путь к появлению шумов на снимке. Повышенная зернистость, появление мозаики – это те черты, которые раздражают и требуют тщательной вторичной обработки изображения.
Уровень светочувствительности является определяющим только при четком осознании того, в каких именно условиях будет использоваться камера. К примеру, при работе со штативом можно покупать фотоаппарат с высоким показателем, это даст широкие возможности съемки при самых разных освещениях без применения вспышки.
Физическая геометрия сенсора
Физический размер матрицы фотоаппарата в миллиметрах – еще один фактор, который не только напрямую отвечает за качество снимков, но и очень сильно формирует цену камеры. У самых лучших моделей соотношение размерности, которое основано на стандартном формате пленки 35 мм, близко к единице. Чем дешевле модель, тем выше показатель “кроп”, обрезки, который сигнализирует о том, что матрица меньше по габаритам.
Чем меньше площадь сенсора, тем ниже охват визуального пространства перед объективом и:
- ниже общее количество света, которое падает на матрицу, следовательно, приходится повышать светочувствительность и увеличивать цифровой шум;
- больше теряется малых деталей, появляется размытие, это вызывают малые размеры, до которых преобразуется кадр.
Высокие значения кропа в фотоаппарате также означают, что разница в освещенности объектов в поле зрения фотоаппарата будет сглаживаться, что очень негативно сказывается на снимках, полученных в вечернее время без вспышки, например.
Коэффициент размерности указывается в документации к камере. Неважно, ориентируетесь ли на бюджетную или профессиональную модель – лучше будет купить аппарат с большой в геометрическом смысле матрицей.
Заключение
Невозможно сказать, какая матрица лучше. Выбирать фотоаппарат следует исходя из режимов, в которых он будет использоваться. Невозможно провести и всесторонне сравнение матриц фотоаппаратов – каждая проиграет в каком-то случае.
Правильно предсказанные условия съемок позволят камерам даже с относительно посредственными матрицами делать очень хорошие снимки. Главный фактор, который нужно учитывать обязательно – геометрические размеры матрицы. Тем, кто хочет получать действительно большие изображения в пикселях, также нужно обратить внимание на количество эффективных мегапикселей фотоаппарата.
Матрица фотоаппарата. Типы и характеристики.
Матрица фотоаппарата самая важная составляющая часть любой камеры. Именно она ответственна за создание изображения, после поступления на ее поверхность светового потока. Если описать матрицу научными словами, то это будет звучать следующим образом, микросхема состоящая из светочувствительных элементов, фотодиодов. Посмотрите следующий снимок, где показано месторасположение матрицы в блоке самого фотоаппарата («тушке»).
Матрица фотоаппарата самым прямым образом влияет на качество итогового изображения, что в сочетании с профессиональным фотообъективом приводит к точной и полной передаче всех деталей реальности.
1. Размер матрицы
2. Количество пикселей
3. Светочувствительность
Теперь подробнее о каждой из указанных характеристик.
Физический размер матрицы, т.е соотношение длины и ширины, измеряемой в миллиметрах, одна из самых важных характеристик матрицы. Чем больше размер, тем лучше будет качество фотографии. Почему? Большая по размеру матрицу, получает больше света, что в свою очередь связано с фактором ISO/светочувствительности. Даже при высоких значения ISO, количество шумов на фотоснимке, сделанном на профессиональную камеру с большой матрицей, будет минимальное. Чего нельзя сказать о фотоснимке сделанном, при участии маленькой матрицы.
Далее на картинке вы можете изучить самые распространенные размера матрицы в соотношение к диагонали.
Количество пикселей в матрице фотоаппарата влияет на размер изображения. Все профессиональные зеркальные фотокамеры снабжены матрицей с большим числом мегапикселей. Как результат, вы сможете распечатать большую фотографию, плакат или постер и все цвета и детали при этом, будут переданы в наилучшем качестве.
Типы матриц фотоаппарата.
По применяемой технологии матрицы бывают нескольких типов, но самые популярные из них:
— ПЗС (CCD — Charge Coupled Device). Данный тип матрицы выпускается практически всеми фирмами производителями фотокамер (Nikon, Canon, Sony и др.). Один из очевидных плюсов высокая чувствительность и маленький уровень шумов, что положительно влияет на качество фотографии, но высокое энергопотребление.
— КМПО (CMOS — Complementary Metal Oxide Semiconductor). Основные плюсы данного вида матрицы низкое энергопотребление и высокое быстродействие. В наши дни данный вид матрицы самый распространенный.
Далее, для примера я привела небольшую сравнительную характеристику фотокамер двух фирм лидеров производителей Nikon и Canon.
Профессиональные фотокамеры Nikon D5 (21,33 Мп), D810a (37,09 Мп) имеют КМОП-матрицу размером 35,9 x 24,0 мм. Компактные фотокамеры, например Nikon CoolPix L340, L2750 снабжены ПЗС матрицей.
Профессиональные фотокамеры Canon EOS – 1D X II Mark (21,5 Мп), EOS 5DS R (50,6 Мп) имеют CMOS матрицу. У Canon даже такие компактные камеры как PowerShot SX720 HS, SX 620HS также работают на КМПО матрице.
На этом я заканчиваю свою статью под названием «Матрица Фотоаппарата», дальше будет еще больше полезных и интересных статей. Подписывайтесь на обновления моего блога, и вы будете первыми получать новые статьи.
Матрица камеры
— обзор
3.2 Получение внутренних параметров камеры и трехмерных координат характерных точек
Предполагая, что мировые трехмерные координаты точки P в пространстве равны P w ( x w , y w , z w ) в опорном кадре камеры, а соответствующие координаты изображения — p ( x p , y p ).Согласно обычной модели камеры-обскуры и искажению объектива [11,12], они связаны следующими уравнениями проекции:
xn = xw / zwyw / zw = xy, r2 = x2 + y2,
xd = xd (1 ) xd (2) = (1 + k1r2 + k2r4) xn + 2p1xy + p2 (r2 + 2×2) p1 (r2 + 2y2) + 2p2xy,
(2) xpyp1 = Kxd (1) xd (2) 1withK = fxα · Fxu00fyv0001.
, где ( u 0 , v 0 ) — главная точка на плоскости изображения, x n и x d — идеальные и фактические координаты изображения p соответственно. f x и f y обозначают эффективное фокусное расстояние, k 1 , k 2 — коэффициенты радиального искажения, а p 1 , p 2 — коэффициенты тангенциального искажения. α — коэффициент перекоса, а K — матрица камеры. Все эти внутренние параметры могут быть получены заранее с помощью некоторых эффективных методов калибровки камеры [13,14], и они считаются фиксированными после калибровки камеры.
Учитывая, что интервал между характерными точками известен, можно получить трехмерные локальные координаты характерных точек в соответствующей системе координат камеры [9], которые обозначаются как aijl и bijr ( i = 1, 2, …, м , j = 1, 2,…, n ) соответственно. Если взять в качестве иллюстрации позу 1 на рис. особая точка b 11 , b 31 согласно RCCF соответственно.
Однако существует одна потенциальная проблема, заключающаяся в том, что выбросы, которые являются центрами характерных точек, извлеченных на изображении, выходят далеко за пределы их наземной истинности, могут не дать нам правильно вычислить трехмерные координаты характерной точки в пространстве. Хотя мы сделали характерные точки на наших целях светящимися, чтобы избежать этой проблемы в большинстве условий, все же существует вероятность того, что центры одной или двух характерных точек будут извлечены с большой ошибкой. В этом состоянии мы должны использовать алгоритм RANSAC [15] для проверки центра всех характерных точек, извлеченных на одном изображении, с целью обнаружения и устранения возможных выбросов заранее, а затем использовать следы, характерные точки с допустимым шумом. , чтобы продолжить калибровку.И в этой статье мы предполагаем, что все извлеченные точки центра являются промежуточными и действительными.
Предположим, что в точке j -е направления единиц цели a , b при LCCF и RCCF равны ajl, bjl и ajr, bjr, соответственно, поэтому их можно вычислить по следующему уравнению:
(3) ajl = amjl-a1jl / amjl-a1jl, bjr = bmjr-b1jr / bmjr-b1jr, (j∈ [1, n]).
% PDF-1.4
%
400 0 объект
>
эндобдж
xref
400 109
0000000016 00000 н.
0000003483 00000 н.
0000003712 00000 н.
0000003748 00000 н.
0000004227 00000 п.
0000004392 00000 н.
0000004535 00000 н.
0000004695 00000 н.
0000004839 00000 н.
0000004968 00000 н.
0000005111 00000 п.
0000005240 00000 п.
0000005383 00000 п.
0000005512 00000 н.
0000005655 00000 н.
0000005784 00000 н.
0000005927 00000 н.
0000006056 00000 н.
0000006199 00000 н.
0000006328 00000 н.
0000006471 00000 н.
0000006601 00000 п.
0000006744 00000 н.
0000006874 00000 н.
0000007017 00000 н.
0000007145 00000 н.
0000007288 00000 н.
0000007416 00000 н.
0000007560 00000 н.
0000007688 00000 н.
0000007832 00000 н.
0000007869 00000 н.
0000008225 00000 н.
0000008617 00000 н.
0000009177 00000 н.
0000009264 00000 н.
0000009367 00000 п.
0000009992 00000 н.
0000010142 00000 п.
0000010556 00000 п.
0000011223 00000 п.
0000012683 00000 п.
0000013991 00000 п.
0000014174 00000 п.
0000014232 00000 п.
0000014655 00000 п.
0000014877 00000 п.
0000015541 00000 п.
0000016841 00000 п.
0000017175 00000 п.
0000017458 00000 п.
0000018776 00000 п.
0000024044 00000 п.
0000024387 00000 п.
0000024994 00000 п.
0000026034 00000 п.
0000026702 00000 п.
0000027149 00000 п.
0000027246 00000 п.
0000027739 00000 п.
0000027993 00000 п.
0000028206 00000 п.
0000029544 00000 п.
0000030846 00000 п.
0000031983 00000 п.
0000032805 00000 п.
0000040421 00000 п.
0000426541 00000 н.
0000429274 00000 н.
0000436155 00000 н.
0000440319 00000 п.
0000440383 00000 п.
0000440769 00000 н.
0000440992 00000 н.
0000441064 00000 н.
0000441174 00000 н.
0000441279 00000 н.
0000441328 00000 н.
0000441450 00000 н.
0000441499 00000 н.
0000441630 00000 н.
0000441678 00000 н.
0000441841 00000 н.
0000441889 00000 н.
0000442010 00000 н.
0000442120 00000 н.
0000442301 00000 н.
0000442349 00000 н.
0000442486 00000 н.
0000442624 00000 н.
0000442772 00000 н.
0000442820 00000 н.
0000442942 00000 н.
0000443060 00000 н.
0000443108 00000 п.
0000443241 00000 н.
0000443289 00000 н.
0000443429 00000 н.
0000443477 00000 н.
0000443525 00000 н.
0000443573 00000 н.
0000443621 00000 н.
0000443669 00000 н.
0000443807 00000 н.
0000443855 00000 н.
0000443992 00000 н.
0000444040 00000 н.
0000444088 00000 н.
0000002476 00000 н.
трейлер
] / Назад 795936 >>
startxref
0
%% EOF
508 0 объект
> поток
h ޔ Smlu ~ X [lf \ h5۵] hFM (/ j * (_ P | a:
S8 $ & | 2f_> а $!% ~ W! =? TjPXP
T6b * 9) mѹzc99f} K?) 7 @ jG: ZZp {ܽ Y7u5n [z | # ʸ 鶨 / o
46zw {| `g, UL? 56Ch ‘؛ ku y
ҳ) = L!> j; H./{‘-RF5LTZr.25XTi%Ci ו * MUɓx% gg) ~; Żaxbx6BzD`
Оценка современных методов калибровки камеры для стандартных диагностических настроек рентгеновского изображения
Selby BP, Sakas G, Groch WD, Stilla U • Позиционирование пациента с помощью самокалибровки рентгеновского детектора для терапии под визуальным контролем. Aust Phys Eng Sci Med. 2011; 34: 391–400.
Артикул
Google Scholar
Маркель П., Ликар Б. Регистрация медицинских изображений 3D и 2D.Докторская диссертация, Университет Любляны; 2010.
Миллер Т., Кинтана Э. Калибровка стереофонической рентгеновской системы для трехмерных измерений. Springer, 2014. С. 201–207.
Rougé A, Picard C, Ponchut C, Trousset Y. Геометрическая калибровка цепочек рентгеновского изображения для трехмерной реконструкции. Comput Med Imaging Graph. 1993; 295–300.
Trucco E, Verri A. Введение в методы трехмерного компьютерного зрения. Прентис Холл Энглвуд Клиффс, 1998.
Moura DC, Barbosa JG, Reis AM, Tavares JMRS. Гибкий подход к калибровке бипланарной рентгенографии позвоночника на обычных радиологических системах. Comput Model Eng Sci. 2010; 115–137.
Schumann S, Thelen B, Ballestra S, Nolte L-P, Buchler P, Zheng G. Калибровка рентгеновского изображения и ее применение в клинической ортопедии. Med Eng Phys. 2014; 36: 968–74.
Артикул
PubMed
Google Scholar
Селби Б., Сакас Г., Уолтер С., Стилла У. Калибровка геометрии рентгеновского оборудования в устройствах для лучевой терапии. 2007. С. 968–974.
де Моура Д.С., Барбоса Дж.М.Г., да Силва Таварес Дж.М.Р., Рейс А. Калибровка биплоскостной рентгенографии с минимальным количеством фантомов. В кн .: Симпозиум по информатике. 2008. С. 1–10.
Medioni G, Kang SB. Новые темы компьютерного зрения. Прентис Холл. 2004.
Бушонг С. Радиологическая наука для технологов: физика, биология и защита.Эльзевир. 2012.
Rowlands JA. Физика компьютерной радиографии. Phys Med Biol. 2002; 47: 123–66.
Артикул
Google Scholar
Доббинс Дж.Т., Эргун Д.Л., Рутц Л., Хиншоу Д.А., Блюм Х., Кларк Д.К. DQE (f) четырех поколений устройств для получения компьютерной рентгенографии. Med Phys. 1995; 22: 1581–93.
Артикул
PubMed
Google Scholar
Хартли Р. Самокалибровка по нескольким изображениям с вращающейся камерой. В: Европейская конференция по компьютерному зрению. 1994. С. 471–478.
Цай Р. Универсальный метод калибровки камеры для высокоточной метрологии трехмерного машинного зрения с использованием стандартных телекамер и объективов. IEEE J Robot Autom. 1985. 3 (4): 323–44.
Артикул
Google Scholar
Хартли Р., Зиссерман А. Множественная геометрия представления в компьютерном зрении.Издательство Кембриджского университета. 2004.
Zhang Z. Новый гибкий метод калибровки камеры. IEEE Trans Pattern Anal Mach Intell. 2000; 22: 1330–4.
Артикул
Google Scholar
Ремондино Ф., Фрейзер К. Методы калибровки цифровых фотоаппаратов: соображения и сравнения. Symposium Image Eng Vis Metrol. 2006; 36: 266–72.
Google Scholar
Zollner H, Sablatnig R. Сравнение методов геометрической калибровки камеры с использованием планарных калибровочных мишеней. В: Цифровые изображения в СМИ и образовании. 2004. С. 237–244.
Гупта М., Упадхьяй С., Нагават А.К. Методика калибровки камеры с использованием алгоритма Цая. В: Международный журнал корпоративных вычислений и бизнес-систем. 2011.
Mckerrow PJ, Abrantes J. Проблемы, возникшие при реализации алгоритма Цая для калибровки камеры.В: Австралазийская конференция по робототехнике и автоматизации. 2002. С. 66–70.
Азиз АЙИ, Карара Х.М. DLT в координаты пространства объекта в фотограмметрии ближнего действия. В: Симпозиум по фотограмметрии ближнего действия. 1971. С. 1–18.
Альбиоль А.Дж., Альбиоль А., Фернандес А., Родриго Дж., Альбиоль Ф. Диспетчерские процедуры и методы работы с физическими объектами, объединяющими средние радиологические системы и профильные камеры. Consejo Superior de Investigaciones Científicas.2012.
Armangué X, Salvi J. Общий взгляд на оценку фундаментальной матрицы. Image Vis Comput. 2003. 21: 205–20.
Артикул
Google Scholar
Луонг Q-T, Фаугерас О. Фундаментальная матрица: теория, алгоритмы и анализ устойчивости. Int J Comput Vision. 1996; 17: 43–75.
Артикул
Google Scholar
Санчес Дж. А., Дестефанис Е. А., Канали, Л. Р..Калибровка камеры по плоскости без алгоритмов прямой оптимизации. IV Хорнадас Аргентинас де Роботика. 2006.
компьютерное зрение — Как я могу рассчитать положение камеры, сравнивая две фотографии?
Я бы посоветовал вам использовать для этого OpenCV. Я также думаю, что этот вопрос больше подошел бы для StackOverflow.
Учебником по этому предмету будет «Многоканальная геометрия» Хартли и Зиссермана. http://www.robots.ox.ac.uk/~vgg/hzbook/ (На этом веб-сайте есть образец главы о фундаментальной матрице.)
По сути, сначала найдите фундаментальную матрицу, а затем, зная внутренние параметры камеры, найдите решение для положения.
Алгоритм
Вот как я бы сделал это в OpenCV. Я делал это раньше, так что это должно сработать.
1. Запустите Feature Detection и Detector Extractor на обоих изображениях.
2. Особенности матча.
3. Используйте F = cv :: findFundamentalMatrix с Ransac.
4. E = K.t () * F * K. // K нужно найти заранее.
5. Выполните разложение по SingularValue для E так, чтобы E = U * S * V.t ()
6. R = U * W.inv () * V.t () // W = [[0, -1, 0], [1, 0, 0], [0, 0, 1]]
7. Tx = V * Z * V.t () // Z = [[0, -1, 0], [1, 0, 0], [0, 0, 0]]
8. получить t из Tx (матричная версия кросс-произведения)
9. Найдите правильное решение. Возможны R.t () и -t.
10. Получите общий масштаб, зная длину кубика Рубрика.
Я уверен, что может сработать и более простой подход. Преимущество этого подхода в том, что не требуется участия человека (без присмотра). Это неверно для необязательного шага 10 (определение масштаба).
Другое решение могло бы использовать знание геометрии куба Рубрика. Например, шесть (5.5) точек необходимы для оценки положения камеры, если известно трехмерное положение точки.
К сожалению, мне неизвестно какое-либо программное обеспечение, которое делает это за вас автоматически.
Вот альтернативный алгоритм:
Запишите координаты углов куба как (X_i, Y_i, Z_i) и, возможно, также точки с другими известными позициями.
Отметьте соответствующие точки u_i = (x_i, y_i).Для каждой корреспонденции создайте две строки в матрице A.
(X_i, Y_i, Z_i, 1, 0, 0, 0, 0, -x_i X_i, -x_i Y_i, -x_i Z_i -x_i)
(0, 0, 0, 0, X_i, Y_i, Z_i, 1, -y_i X_i, -y_i Y_i, -y_i Z_i -y_i)
Затем найдите p такое, что Ap = 0. Т.е. p — правое ядро A или решение Ap = 0 с наименьшими квадратами.
De-Flatten p, чтобы создать матрицу 3×4. С.
Камера
— Как получить матрицу проекции из данных одометрии / тф?
Вы уверены, что хотите проекционную матрицу? Матрица проекции камеры обычно представляет собой матрицу 3×4, которая проецирует (однородные) точки в R 3 на (однородные) точки в R 2 в плоскости изображения в некотором масштабе (см. Запись в википедии).Похоже, вы заинтересованы в сравнении вашей вычисленной визуальной одометрии с одометрией наземной истинности, представленной на веб-сайте KITTI; в этом случае вы будете сравнивать жесткие матрицы преобразования из вашей оценки VO с наземным истинным преобразованием KITTI.
Если вы используете «сырые» наборы данных, «наземная истина» предоставляется в виде записей данных OXTS, т. Е. Комбинированных данных IMU и GPS. Эти данные находятся в глобальном фрейме, и потребуется немного больше работы для сравнения с вашими данными.Однако похоже, что вы используете данные теста одометрии; основные преобразования уже находятся в кадре левой камеры, что должно немного облегчить задачу (и это то, что я буду обсуждать).
Поскольку вы не указали язык, я буду говорить здесь в более общем плане, но ROS действительно предоставляет инструменты на C ++ (tf и Eigen) и Python (transformations.py) для выполнения таких задач, как преобразование из кватернионов в матрицы вращения …
У вас есть t и q , перемещение и вращение представлены в виде кватерниона.Вы можете преобразовать кватернион в матрицу вращения (обычно в форму sxyz) и наоборот. Данные KITTI задаются как матрица 3×4, и это матрица вращения, объединенная с вектором трансляции (т. Е. 4-й столбец t gt ).
r 11 r 12 r 13 t 1
r 21 r 22 r 23 t 2
r 31 r 32 r 33 t 3
Вы можете просто вычислить ошибку перевода, вычислив норму L2: || t — t gt ||.Вычислить ошибку вращения немного сложнее; один из способов сделать это — использовать такую функцию, как QuaternionBase :: angularDistance () из Eigen, поскольку оба измерения должны быть в одной системе координат. Для этого вам нужно преобразовать матрицу вращения наземной истины в кватернион, используя либо Eigen, либо библиотеку transformations.py.
Имейте в виду, что это ошибка в кадре одометрии — то есть ошибка вашей i-й оценочной позы относительно i-й основной истинной позы в кадре исходной позы.Иногда также полезно сравнить среднюю ошибку от кадра к кадру, особенно потому, что одометрия имеет тенденцию к значительному смещению со временем, даже если алгоритм относительно точен в среднем между кадрами.
Итого:
- преобразовать матрицы вращения в кватернионы для вычисления угловой ошибки (обратите внимание на системы координат),
- и используйте формулу || t — t gt || для вычисления ошибки перевода.
- снова, обратите внимание на свои системы координат.
Матрицы преобразования цветов в цифровых камерах: учебное пособие
1.
Введение
Рассмотрите возможность преобразования сцены, снятой цифровой камерой в необработанном пространстве камеры, в цифровое изображение, подходящее для отображения с использованием цветового пространства, ориентированного на вывод. По крайней мере, есть два принципиально важных вопроса, которые необходимо решить, пытаясь правильно воспроизвести внешний вид цвета. Во-первых, функции отклика цифровых фотоаппаратов отличаются от функций зрительной системы человека (HVS).Широко используемый подход к этой проблеме состоит в том, чтобы рассматривать цветовые пространства как векторные пространства и учитывать различия в ответах путем введения матрицы преобразования цветов. Типом матрицы преобразования цвета, который обычно встречается, является матрица характеристик 3 × 3 T_, которая определяет линейную взаимосвязь между необработанным пространством камеры и эталонным цветовым пространством CIE XYZ:
В целом, необработанные пространства камеры не являются колориметрическими, поэтому преобразование приблизительное. Отношения могут быть оптимизированы для данного источника света путем минимизации цветовой ошибки.Примечательно, что это означает, что оптимальная T_ зависит от характера источника света сцены, 1 , 2 , включая его точку белого (WP). Методология характеристики для определения оптимального T_ описана в разд. 2.4, вместе с иллюстрацией того, как T_ следует нормализовать на практике.
Вторая проблема, которую необходимо решить, — это восприятие освещения сцены WP. Хотя различные механизмы адаптации, используемые HVS, сложны и не до конца понятны, считается, что HVS естественным образом использует механизм хроматической адаптации для регулировки своего восприятия WP освещения сцены для достижения постоянства цвета при различных условиях освещения. 3 , 4 Поскольку датчики цифровых камер не адаптируются естественным образом, неправильный баланс белого (WB) будет возникать, когда WP освещения сцены отличается от эталонного белого цветового пространства, связанного с выходом, используемого для кодировать выходное изображение, созданное камерой. Как показано в разд. 3, цифровые камеры должны пытаться имитировать этот механизм хроматической адаптации, используя соответствующее преобразование хроматической адаптации (CAT).
Как обсуждалось в разд.4, современные смартфоны и коммерческие необработанные преобразователи обычно вычисляют оптимальную характеристическую матрицу T_ путем интерполяции между двумя предварительно установленными характеристическими матрицами в соответствии с оценкой WP освещения сцены, и CAT реализуется после применения T_. В традиционных цифровых камерах преобразование цвета обычно переформулируется в терминах множителей необработанных каналов и матриц вращения цвета R_. Этот подход предлагает несколько преимуществ, как обсуждалось в разд. 5. Аналогичный, но более простой в вычислительном отношении подход используется конвертером исходных файлов DCRaw с открытым исходным кодом, как обсуждалось в разд.6. Конвертер цифровых негативов Adobe ® с открытым исходным кодом (DNG) предлагает два метода преобразования цветов, и природа цветовых матриц Adobe и прямых матриц обсуждается в разд. 7. Наконец, в разд. 8.
2.
Camera Raw Space
2.1.
Gamut
Необработанное пространство камеры для данной модели камеры возникает из ее набора функций спектральной чувствительности или функций отклика камеры:
Eq. (2)
Ri (λ) = QEi (λ) eλhc, где e — заряд элемента, λ — длина волны, h — постоянная Планка, а c — скорость света.Внешний квантовый выход для мозаики i определяется уравнением
. (3)
QEi (λ) = TCFA, i (λ) η (λ) T (λ) FF, где TCFA, i — функция пропускания матрицы цветных фильтров (CFA) для мозаики i, η (λ) — заряд эффективность сбора или внутренняя квантовая эффективность фотоэлемента, а T (λ) — функция пропускания границы раздела SiO2 / Si. 5 Коэффициент заполнения определяется как FF = Adet / Ap, где Adet — это светочувствительная область обнаружения на фотосайте, а Ap — это площадь фотосайта. Спектральная полоса пропускания камеры должна идеально соответствовать видимому спектру, поэтому требуется фильтр, блокирующий инфракрасное излучение.
Аналогично функциям отклика конуса глаза HVS, которые можно интерпретировать как определение количества основных цветов конуса глаза, которые глаз использует для восприятия цвета при заданном λ, функции отклика камеры можно интерпретировать как указание количества основные цвета необработанного пространства камеры на каждом λ. Например, измеренные функции отклика камеры Nikon D700 показаны на рис. 1. Однако необработанное пространство камеры является колориметрическим только в том случае, если выполняется условие Лютера-Айвса, 7 — 9 , что означает, что функция отклика камеры должно быть точным линейным преобразованием функций отклика конуса глаза, которые косвенно представлены как линейное преобразование из функций согласования цвета CIE для стандартного наблюдателя.
Рис. 1
Функции отклика камеры Nikon D700. Пиковая спектральная чувствительность нормирована на единицу. Данные получены из исх. 6.
Хотя функции отклика конуса глаза подходят для захвата деталей с помощью простого объектива человеческого глаза, в цифровых камерах используются составные линзы, которые были скорректированы на хроматическую аберрацию. Следовательно, функции отклика камеры разработаны с учетом других соображений. 10 , 11 Например, лучшее соотношение сигнал / шум достигается за счет уменьшения перекрытия функций отклика, что соответствует характеристической матрице с меньшими недиагональными элементами. 10 — 12 Действительно, незначительные цветовые ошибки могут быть заменены на лучшее соотношение сигнал / шум. 10 — 13 С другой стороны, повышенная корреляция в измерении длины волны может улучшить производительность процедуры цветовой демозаики. 14 Из-за таких компромиссов наряду с ограничениями производства фильтров, функции отклика камеры на практике не являются точными линейными преобразованиями функций отклика конуса глаза.Следовательно, необработанные пространства камеры не являются колориметрическими, поэтому камеры показывают метамерную ошибку. Метамеры — это разные спектральные распределения мощности (SPD), которые HVS воспринимают как один и тот же цвет при просмотре в одинаковых условиях. Камеры с метамерной ошибкой дают разные цветовые отклики на эти метамеры. Метамерная ошибка камеры может быть определена экспериментально и количественно оценена с помощью индекса метамерии чувствительности цифровой фотокамеры (DSC / SMI). 8 , 15
На рисунке 2 показан спектральный локус HVS на диаграмме цветности xy, которая представляет собой двумерную проекцию цветового пространства CIE XYZ, которая описывает относительные пропорции трехцветных значений.Обратите внимание, что сам спектральный локус имеет форму подковы, а не треугольника из-за того, что перекрытие функций отклика глаз-конус предотвращает независимую стимуляцию глазных колбочек, поэтому цветности, соответствующие координатам цветности (x, y), расположены за пределами спектральные локусы невидимы или воображаемы, поскольку они более насыщены, чем чистые цвета спектра. Цветовой охват необработанного пространства камеры Nikon D700 также показан на рис. 2 и сравнивается с несколькими стандартными цветовыми пространствами для вывода, а именно sRGB, 16, Adobe ® RGB, 17 и ProPhoto RGB. 18 Из-за положений основных цветов необработанного пространства камеры на диаграмме цветности xy, некоторые области гаммы необработанного пространства камеры не достигают спектрального геометрического места HVS, поскольку эти области лежат за пределами треугольной формы, доступной для аддитивных линейных комбинаций три праймериз. Кроме того, заметным следствием метамерной ошибки камеры является то, что необработанная пространственная гамма камеры искажается от треугольной формы, доступной для аддитивных линейных комбинаций трех основных цветов.Некоторые области даже вытеснены за пределы треугольника, доступного для цветового пространства CIE XYZ. 19 См. Исх. 19 для дополнительных примеров.
Рис. 2
Цветовая гамма необработанного пространства камеры для Nikon D700 (голубая заштрихованная область), нанесенная на диаграмму цветности xy. Цветовая гамма не является идеальным треугольником, поскольку нарушается условие Лютера-Айвса, что также объясняет, почему определенные области выталкиваются за пределы треугольника, доступного для цветового пространства CIE XYZ, определенного основными цветами, расположенными в (0,0), (0,1 ) и (1,0).Граница серой заштрихованной области в форме подковы определяет спектральный локус HVS. Насыщенность уменьшается по мере удаления от спектрального локуса внутрь. Для сравнения указаны (треугольные) гаммы нескольких цветовых пространств, относящихся к стандартному выводу.
Чтобы определить гамму необработанного пространства камеры, первым шагом является измерение функций отклика камеры с использованием монохроматора на дискретном наборе длин волн в соответствии с методом A стандарта ISO 17321-1. 15 Для каждой длины волны функции отклика камеры выдают необработанные относительные трехцветные значения RGB в необработанном пространстве камеры.Второй шаг — преобразовать RGB в относительные значения CIE XYZ путем применения матрицы характеристик, которая удовлетворяет уравнению. (1). Впоследствии координаты цветности (x, y), соответствующие спектральному локусу необработанного пространства камеры, могут быть вычислены с использованием обычных формул, x = X / (X + Y + Z) и y = Y / (X + Y + Z ).
Так как заданная матрица характеристик оптимизирована для использования с освещающим источником, то есть освещением сцены, используемым для выполнения характеристики, другим следствием метамерной ошибки камеры является то, что необработанная пространственная гамма камеры может изменяться в зависимости от применяемой матрицы характеристик.Палитра необработанного пространства камеры Nikon D700, показанная на рис. 2, была получена с использованием матрицы характеристик, оптимизированной для источника света D65 CIE. На рисунке 3 показано, как изменяется цветовая гамма, когда вместо нее применяется матрица характеристик, оптимизированная для источника A CIE.
Рис. 3
То же, что и на рис. 2, за исключением того, что для получения необработанного пространственного охвата камеры использовалась матрица характеристик, оптимизированная для источника света CIE A, а не матрица характеристик, оптимизированная для источника света CIE D65.
2.2.
Необработанные значения
Значения цвета в необработанном пространстве камеры выражаются в виде цифровых необработанных значений для каждого необработанного цветового канала, которые аналогичны трехцветным значениям в цветовом пространстве CIE. Для CFA, который использует три типа цветных фильтров, таких как CFA Байера, 20 , необработанные значения, выраженные с использованием единиц, относящихся к выходу, т. Е. Данных / цифровых чисел (DN) или аналого-цифровых единиц, относятся к следующим набор необработанных каналов, обозначенных здесь каллиграфическими символами:
Eq.(4)
[nDN, 1nDN, 2nDN, 3nDN, 4] = [RG1G2B]. Хотя здесь для представления блока Байера использовалась векторная нотация, истинный необработанный вектор пикселей получается только после выполнения цветной демозаики в в этом случае с каждым фотосайтом будет связано четыре необработанных значения. CFA Байера использует в два раза больше зеленых фильтров, чем красный и синий, что означает, что в целом будут получены два значения G1 и G2, связанные с разными позициями в каждом блоке Байера. Это выгодно с точки зрения общего отношения сигнал / шум, поскольку фотосайты, принадлежащие зеленой мозаике, более эффективны с точки зрения фотопреобразования.Кроме того, шаблон Байера оптимален с точки зрения уменьшения артефактов наложения спектров, когда три типа фильтров расположены на квадратной сетке. 14 Хотя считается, что большее количество зеленых фильтров обеспечивает повышенное разрешение для сигнала яркости, поскольку стандартная функция яркости 1924 CIE для пиков фотопического зрения на 555 нм, 20 утверждалось, что CFA Байера с двукратным увеличением больше синих пикселей, чем красных и зеленых было бы оптимальным для этой цели. 14 При демозаике необработанных данных, соответствующих стандартному CFA Байера, окончательный результат покажет ложные лабиринты или сетки, если соотношение между G1 и G2 изменяется по изображению. 21 Программные необработанные преобразователи могут усреднять G1 и G2 вместе, чтобы устранить такие артефакты. 21
Поскольку в принципе существует только три функции отклика камеры, R1 (λ), R2 (λ) и R3 (λ), цветовая характеристика для CFA Байера рассматривает G1 и G2 как один канал, G. Необработанные значения можно выразить следующим образом:
Ур.(5)
R = k∫λ1λ2R1 (λ) E˜e, λdλ, G = k∫λ1λ2R2 (λ) E˜e, λdλ, B = k∫λ1λ2R3 (λ) E˜e, λdλ. Функции отклика камеры определены формулой. В уравнении (2) интегрирование производится по спектральной полосе пропускания камеры, E˜e, λ — средняя спектральная освещенность на фотосайте, а k — постоянная величина. Выражения для E˜e, λ и k приведены в Приложении.
Фактические необработанные значения, полученные на практике, представляют собой квантованные значения, смоделированные путем взятия целой части уравнения. (5). При преобразовании из необработанного пространства камеры полезно нормализовать исходные значения до диапазона [0,1] путем деления уравнения.(5) необработанной точкой отсечения, которая является наивысшим доступным DN.
2.3.
Эталонный белый
Используя приведенную выше нормализацию, эталонный белый цвет необработанного пространства камеры определяется единичным вектором
, выраженным в терминах трехцветных значений CIE XYZ или координат цветности (x, y) с Y = 1, эталонный белый необработанного пространства камеры — это WP освещения сцены, которая дает максимально равные исходные значения для нейтрального объекта. (WP SPD определяется трехцветными значениями CIE XYZ, которые соответствуют 100% нейтральному диффузному отражателю, освещенному этим SPD.)
Отсюда следует, что эталонный белый цвет необработанного пространства камеры в принципе можно определить экспериментально, найдя источник света, который дает равные исходные значения для нейтрального объекта. Обратите внимание, что если для декодирования необработанного файла используется конвертер RAW с открытым исходным кодом DCRaw, необходимо отключить WB. С точки зрения колориметрии CIE, эталонный белый цвет необработанного пространства камеры формально определяется формулой
Eq. (7)
[X (WP) Y (WP) Z (WP)] сцена = T_ [R (WP) = 1G (WP) = 1B (WP) = 1] сцена, где Y (WP) = 1 и нижние индексы означают, что WP — это точка освещения сцены.Матрица характеристик 3 × 3 T_ преобразуется из необработанного пространства камеры в CIE XYZ и должна быть оптимизирована для требуемого освещения сцены. Оптимальное значение T_ на данном этапе неизвестно, но в принципе может быть определено с помощью процедуры оптимизации, описанной в разд. 2.4.
Хотя цветовые пространства CIE используют нормализованные единицы, так что их эталонные белые цвета соответствуют WP стандартных источников света CIE, необработанные пространства камеры не нормализуются естественным образом таким образом. Следовательно, эталонный белый цвет необработанного пространства камеры не обязательно является нейтральным цветом, поскольку он обычно расположен далеко от планковского локуса и поэтому не обязательно имеет связанную коррелированную цветовую температуру (CCT).
Обратите внимание, что WP может быть связан с CCT при условии, что его координаты цветности (x, y) достаточно близки к планковскому локусу, но существует много таких координат, которые соответствуют одной и той же CCT. Чтобы различать их, может быть присвоено значение Duv, неофициально называемое цветовым оттенком. 22 Это определяется путем преобразования (x, y) в координаты цветности (u, v) на диаграмме цветности UCS CIE 1960, 23 , 24 , где изотермы нормальны для локуса Планка.В этом представлении CCT является допустимой концепцией только для координат (u, v), расположенных на расстоянии от планковского локуса, которое находится в пределах Duv = ± 0,05 вдоль изотермы. 25
Чтобы увидеть, что эталонный белый цвет необработанного пространства камеры далек от планковского локуса, рассмотрим исходные значения Nikon D700 для нейтрального диффузного отражателя, освещенного источниками освещения CIE A и D65, соответственно,
Eq. (8)
[R (WP) = 0,8878G (WP) = 1,0000B (WP) = 0,4017] A = T_A − 1 [X (WP) = 1,0985Y (WP) = 1,0000Z (WP) = 0.3558] A [R (WP) = 0,4514G (WP) = 1,0000B (WP) = 0,8381] D65 = T_D65−1 [X (WP) = 0,9504Y (WP) = 1,0000Z (WP) = 1,0888] D65, где T_A и T_D65 — это примерные характеристические матрицы, оптимизированные для осветительных приборов CIE A и D65, соответственно. Как показано на рис. 4, WP этих стандартных источников света очень близки к планковскому локусу. Источник света A имеет CCT = 2856 K и Duv = 0,0, а источник света D65 имеет CCT = 6504 K и Duv = 0,0032. Очевидно, что приведенные выше необработанные значения Nikon D700 сильно отличаются от единичного вектора необработанного пространства камеры, и в обоих случаях необходимо применить большие множители к необработанным значениям красных и синих пикселей.Эти множители известны как умножители необработанных каналов, поскольку они обычно применяются к необработанным красным и синим каналам перед цветовой демозаикой как часть стратегии преобразования цвета, используемой внутренними механизмами обработки изображений традиционных цифровых камер.
Рис. 4
Расчетные эталонные белые пространства необработанных пространств фотокамер Nikon D700 и Olympus E-M1 по сравнению с WP осветительных приборов CIE A и D65. Планковский локус представлен черной кривой. Цветом отображаются только видимые цветности, содержащиеся в цветовом пространстве sRGB.
Оценка эталонного белого цвета Nikon D700 может быть получена путем аппроксимации уравнения. (7) с использованием легко доступной матрицы характеристик вместо T_. Применение T_A дает (x, y) = (0,3849,0,3058), что соответствует Duv = -0,0378. Это связано с CCT = 3155 K, так как значение Duv находится в пределах допустимого предела, но на рис. 4 показано, что цветовой оттенок является сильным пурпурным. Это справедливо для типичных пространств необработанного снимка в целом. 21 Аналогичная оценка для камеры Olympus E-M1 дает (x, y) = (0.3599,0,2551), что соответствует Duv = −0,0637. У этого нет связанной CCT, а цветовой оттенок — очень сильный пурпурный.
Хотя тот факт, что эталонные белые цвета необработанного пространства камеры не являются нейтральными с точки зрения колориметрии CIE, не влияет на окончательное воспроизводимое изображение, он будет показан в разд. 5 видно, что эталонный белый цвет необработанного пространства камеры используется в качестве полезного промежуточного шага в стратегии преобразования цвета, используемой традиционными цифровыми камерами.
2.4.
Цветовая характеристика камеры
Вспомните линейное преобразование из необработанного пространства камеры в CIE XYZ, определенное уравнением.(1):
, где T_ — матрица характеристик 3 × 3:
Eq. (9)
T _ = [T11T12T13T21T22T23T31T32T33]. Преобразование цветов является приблизительным, поскольку условие Лютера-Айвса не выполняется точно. Как упомянуто во введении, T_ может быть оптимизирован для характеристического источника света, то есть освещения сцены, используемого для выполнения характеризации. 1 , 2 Оптимальная матрица T_ зависит от самого SPD, но в значительной степени зависит от характеристического освещения WP при условии, что источник света представляет реальный SPD.
Матрицы характеристик, оптимизированные для известных источников света, могут быть определены с помощью процедур минимизации цветовых ошибок, основанных на фотографиях, сделанных на стандартной цветовой диаграмме. 2 Хотя были разработаны различные методы минимизации, включая методы сохранения WP, 26 процедура, описанная ниже, основана на стандартизированном методе B ISO 17321-1. 15
Обратите внимание, что ISO 17321-1 использует обработанные изображения, выводимые камерой, а не необработанные данные, и, следовательно, требует инверсии функции оптоэлектронного преобразования камеры (OECF). 27 OECF определяет нелинейную взаимосвязь между освещенностью на плоскости датчика и уровнями цифрового вывода видимого выходного изображения, такого как файл JPEG, созданный камерой. Чтобы обойти необходимость экспериментального определения OECF, ниже описывается вариант метода B из ISO 17321-1. В этом методе для декодирования необработанного файла используется конвертер исходных данных с открытым исходным кодом DCRaw, чтобы исходные данные можно было использовать напрямую. 28 , 29
1.Сделайте снимок таблицы цветов, освещенной указанным источником света. Поскольку исходные значения масштабируются линейно, важны только их относительные значения. Однако число f N и продолжительность экспозиции t следует выбирать так, чтобы избежать клиппирования.
2. Рассчитайте относительные значения тристимула XYZ для каждого участка цветовой диаграммы:
Eq. (10)
X = k∫λ1λ2x¯ (λ) Ee, λR (λ) dλY = k∫λ1λ2y¯ (λ) Ee, λR (λ) dλZ = k∫λ1λ2z¯ (λ) Ee, λR (λ) dλ , где Ee, λ — спектральная освещенность, падающая на цветовую диаграмму, измеренная с помощью спектрометра; x¯ (λ), y‾ (λ) и z¯ (λ) — функции согласования цветов цветового пространства CIE XYZ; и интегрирование дискретизируется в сумму с шагом 10 нм и ограничивает λ1 = 380 нм и λ2 = 780 нм.Если не используется трехцветный колориметр, расчет требует знания спектральной отражательной способности каждого участка. Спектральная отражательная способность в приведенных выше уравнениях обозначена R (λ), и ее не следует путать с функциями отклика камеры. Константу нормализации k можно выбрать так, чтобы Y находился в диапазоне [0,1] с использованием белого пятна в качестве белого эталона.
3. Получите линейное выходное изображение с демозаикой прямо в необработанном пространстве камеры без преобразования в любое другое цветовое пространство.Гамма-кодирование, кривые тона и баланс белого должны быть отключены. Поскольку настоящий метод позволяет обойтись без необходимости определять и инвертировать OECF, очень важно отключить WB; в противном случае к необработанным каналам могут применяться множители сырых каналов. При использовании конвертера RAW с открытым исходным кодом DCRaw подходящей командой является
dcraw -v -r 1 1 1 1-o 0 -4 -T filename. Это дает 16-битный линейный выходной файл TIFF с демозаикой в необработанном пространстве камеры. Если вы работаете с необработанными каналами, а не с необработанными пиксельными векторами с демозаикой, подходящей командой является dcraw -v -D -4 -T filename.Вышеупомянутые команды DCRaw объяснены в таблице 3.
4. Измерьте средние значения R, G и B по блоку пикселей размером 64 × 64 в центре каждого фрагмента. Затем каждый патч может быть связан с соответствующим средним необработанным вектором пикселей.
5. Постройте матрицу A_ 3 × n, содержащую векторы цветового пространства XYZ для каждого фрагмента 1,…, n в виде столбцов:
Eq. (11)
A _ = [X1X2 ⋯ XnY1Y2 ⋯ YnZ1Z2 ⋯ Zn]. Точно так же постройте матрицу B_ 3 × n, содержащую соответствующие необработанные векторы пикселей в виде столбцов:
Eq.(12)
B _ = [R1R2 ⋯ RnG1G2 ⋯ GnB1B2 ⋯ Bn].
6. Оцените характеристическую матрицу 3 × 3 T_, которая преобразует B_ в A_:
Предварительное решение получается с использованием минимизации линейных наименьших квадратов: 2 , 15
Ур. (14)
T_ = A_B_T (B_B_T) -1, где верхний индекс T обозначает оператор транспонирования.
7. Используйте предварительную оценку T_, чтобы вычислить новый набор оцененных значений тристимула CIE XYZ A_ ‘в соответствии с формулой. (13).Преобразуйте A_ и A′_ в перцептивно однородное эталонное цветовое пространство CIE LAB и вычислите цветовую разницу ΔEi между оцененными значениями трехцветного стимула и реальными значениями трехцветного стимула для каждого фрагмента i. Набор {ΔEi} можно использовать для вычисления DSC / SMI. 8 , 15 Обратите внимание, что для точного удовлетворения условия Лютера-Айвса необходимо, чтобы A _ ′ = A_, и в этом случае будет получен показатель DSC / SMI, равный 100.
8. Оптимизируйте T_, минимизируя {ΔEi}, используя метод нелинейной оптимизации, рекомендованный ISO 17321-1.Окончательный DSC / SMI определяет окончательную потенциальную цветовую ошибку. В идеале, включите ограничение, которое сохраняет характеристический источник света WP.
9. Масштабируйте окончательный T_ в соответствии с нормализацией, необходимой для его практического применения. Это обсуждается ниже.
Если WB был отключен на шаге 3, характеристическая матрица T_ может использоваться с произвольным освещением сцены. Тем не менее, оптимальные результаты будут получены для освещения сцены с помощью WP, который точно соответствует таковой характеристического источника света.
На рисунке 5 показано, как матричные элементы оптимизированной матрицы характеристик изменяются в зависимости от CCT характеристического источника света для камеры Olympus E-M1.
Рис. 5
Изменение элементов матрицы характеристической матрицы для камеры Olympus E-M1 в зависимости от характеристического источника света CCT.
Для той же камеры на рис. 6 (a) показана фотография цветовой диаграммы в необработанном пространстве камеры, сделанная при освещении D65. Когда значения RGB необработанного пространства камеры интерпретируются как значения RGB в цветовом пространстве sRGB для целей отображения без применения какой-либо матрицы цветовых характеристик, проявляется сильный оттенок зеленого цвета, который возникает из-за большей передачи зеленого фильтра Байера.На рисунке 6 (b) показана та же фотография, преобразованная в цветовое пространство sRGB путем применения оптимизированной матрицы характеристик T_, за которой следует матрица, преобразующая цвета из цветового пространства CIE XYZ в sRGB. Видно, теперь цвета отображаются правильно.
Рис. 6
(a) Фотография цветовой диаграммы в необработанном пространстве камеры, сделанная при освещении D65. (b) Та же фотография, преобразованная в цветовое пространство sRGB.
2,5.
Нормализация матрицы характеристик
Нормализация матрицы характеристик относится к масштабированию всей матрицы таким образом, чтобы все элементы матрицы масштабировались одинаково.Типичная нормализация, применяемая на практике, заключается в том, чтобы гарантировать, что матричные карты между характеризующим источником света WP, выраженным с использованием цветового пространства CIE XYZ, и необработанным пространством камеры, так что необработанные данные просто насыщаются, когда 100% нейтральный диффузный отражатель фотографируется под характеризующим источником света. . Зеленый необработанный канал обычно насыщается первым.
Например, если характеристический источник света — D65, то T_ может быть нормализовано таким образом, чтобы его обратное значение обеспечивало следующее отображение:
Eq.(15)
[R (WP) G (WP) B (WP)] D65 = T_ − 1 [X (WP) = 0,9504Y (WP) = 1,0000Z (WP) = 1,0888] D65, где max {R ( WP), G (WP), B (WP)} = 1. Поскольку необработанный зеленый канал обычно первым насыщается при большинстве типов освещения, обычно бывает, что G (WP) = 1, тогда как R (WP) <1 и B (WP) <1.
Например, матрицы характеристик Olympus E-M1, используемые на рис. 5 для калибровочных осветительных приборов 4200 и 6800 K, определяются формулой
Eq. (16)
T_4200 K = [0,86800,33950,21330,28830,8286-0,02160.0425−0.26471.7637], T_6800 K = [1.21050.25020.18820.45860.8772−0.13280.0936−0.27881.9121]. Эти матрицы нормализованы так, что WP характеристического источника света отображается в исходные значения, где зеленый необработанный канал только достигает насыщения. :
Ур. (17)
[R (WP) = 0,6337G (WP) = 1,0000B (WP) = 0,5267] 4200 K = T_4200 K − 1 [X (WP) = 1,0019Y (WP) = 1,0000Z (WP) = 0,6911 ] 4200 K, [R (WP) = 0,4793G (WP) = 1,0000B (WP) = 0,7312] 6800 K = T_6800 K − 1 [X (WP) = 0,9682Y (WP) = 1,0000Z (WP) = 1,1642 ] 6800 K.
3.
Баланс белого
Замечательным свойством HVS является его способность естественным образом приспосабливаться к условиям окружающего освещения.Например, если на снимке, освещенном дневным светом, установить 100% нейтральный диффузный отражатель, отражатель будет иметь нейтральный белый цвет. Позже в тот же день, когда происходит изменение цветности или CCT освещения сцены, можно ожидать, что цвет отражателя изменится соответствующим образом. Однако отражатель по-прежнему будет иметь нейтральный белый цвет. Другими словами, воспринимаемый цвет объектов остается относительно постоянным при различных типах освещения сцены, что известно как постоянство цвета. 3 , 4
Механизм хроматической адаптации, с помощью которого HVS обеспечивает постоянство цвета, сложен и не до конца понятен, но упрощенное объяснение состоит в том, что HVS направлен на снижение цветности источника света. 30 Еще в 1902 году фон-Крис постулировал, что это достигается за счет независимого масштабирования каждой функции отклика конуса глаза. 3 , 4 Цветовой стимул, который наблюдатель, адаптированный к окружающим условиям, считает нейтральным белым (идеально ахроматическим со 100% относительной яркостью), определяется как адаптированный белый. 31
Поскольку функции отклика камеры естественным образом не имитируют HVS за счет дисконтирования цветности освещения сцены, выходное изображение будет выглядеть слишком теплым или слишком холодным, если оно отображается с использованием освещения с WP, которое не соответствует адаптированному белому для фотографической сцены во время съемки. Это называется неправильным ББ. Проблема может быть решена путем реализации следующей вычислительной стратегии.
1. Сообщите камере об адаптированном белом цвете, прежде чем делать снимок.Из-за сложной зависимости истинно адаптированного белого от окружающих условий эта задача на практике заменяется более простой задачей, а именно идентифицировать освещение сцены WP. Например, предустановка баланса белого, соответствующая освещению сцены, может быть выбрана вручную, оценка CCT освещенности сцены может быть введена вручную, или камера может вычислить свою собственную оценку путем анализа необработанных данных с использованием автоматической функции баланса белого. Во всех случаях оценка камеры для WP освещения сцены известна как нейтральный 32 камеры или принятый белый (AW). 31 (Этот этап оценки освещенности не следует путать с WB. Оценка освещенности относится к вычислительным подходам, используемым автоматической функцией WB для оценки освещенности сцены WP. Очень простой подход к оценке освещенности — это метод «серого мира», 33 , который предполагает, что среднее значение всех цветов сцены окажется ахроматическим.Другой простой подход состоит в предположении, что самый яркий белый, вероятно, будет соответствовать освещению сцены WP. 34 Однако практические алгоритмы оценки освещенности намного сложнее. 35 , 36 )
2. Выберите стандартный эталонный белый цвет, который будет использоваться при отображении выходного изображения. Если изображение будет отображаться с использованием стандартного цветового пространства, связанного с выводом, такого как sRGB, выбранный эталонный белый будет соответствовать цветовому пространству с указанием вывода, которым в случае sRGB является источник света CIE D65.
3.Хроматически адаптируйте цвета изображения, адаптируя оценку WP освещения сцены (AW) так, чтобы он стал опорным белым для выбранного цветового пространства, ориентированного на вывод. Этот шаг балансировки белого достигается применением CAT.
CAT необходимо применять как часть общего преобразования цвета из необработанного пространства камеры в выбранное цветовое пространство, относящееся к выходу. Существуют разные подходы к объединению этих компонентов. Типичный подход, используемый в науке о цвете, — это преобразование из необработанного пространства камеры в CIE XYZ, применение CAT, а затем преобразование в выбранное цветовое пространство, указанное на выходе.В случае sRGB,
Eq. (18)
[RLGLBL] D65 = M_sRGB − 1 CAT_AW → D65 T_ [RGB] сцена, где T_ — это матрица характеристик, которая преобразует необработанное пространство камеры в CIE XYZ и оптимизирована для сцены AW, матрица CAT_AW → D65 в цветовом пространстве CIE XYZ применяется CAT, который адаптирует AW к эталонному белому D65 цветового пространства sRGB, и, наконец, M_sRGB-1 — это матрица, которая преобразует из CIE XYZ в линейную форму цветового пространства sRGB:
Eq . (19)
M_sRGB − 1 = [3,24 · 10−1.5374-0.4986-0.96921.87600.04160.0556-0.20401.0570]. В частности, AW в необработанном пространстве камеры сопоставляется с эталонным белым цветовым пространством, указанным на выходе, определенным единичным вектором в цветовом пространстве, указанном на выходе. :
Ур. (20)
[RL = 1GL = 1BL = 1] D65 = M_sRGB − 1 CAT_AW → D65 T_ [R (AW) G (AW) B (AW)] сцена. Когда закодированное выходное изображение просматривается на откалиброванном мониторе. , объект сцены, который HVS считал белым на момент съемки фотографии, теперь будет отображаться с использованием эталонного белого цвета D65.В идеале окружающие условия просмотра должны соответствовать условиям, определенным как подходящие для просмотра цветового пространства sRGB.
Если оценка WP освещения сцены далека от истинного WP освещения сцены, то для HVS будет очевиден неверный WB. Если оценка CCT освещенности сцены выше, чем истинная CCT, фотография будет выглядеть слишком теплой. И наоборот, если оценка CCT освещенности сцены ниже, чем истинная CCT, тогда фотография будет выглядеть слишком холодной.
На рис. 7 (а) показана фотография цветовой диаграммы, сделанная при вольфрамовом освещении 2700 K CCT с помощью камеры Olympus E-M1.Матрица характеристик T_ была применена для преобразования цветов в CIE XYZ, а затем M_sRGB-1 для преобразования цветов в sRGB. Очевидно, истинный цвет освещения сцены выявляется, поскольку хроматическая адаптация камерой не выполняется. Другими словами, фотография выглядит слишком теплой по сравнению с эталонным белым цветом D65 в цветовом пространстве sRGB. На рисунке 7 (b) показана та же фотография после балансировки белого путем включения CAT, который хроматически адаптирует освещение сцены WP к эталонному белому цветовому пространству sRGB D65, имеющему 6504 K CCT и Duv = 0.0032 цветовой оттенок.
Рис. 7
(a) Фотография цветовой диаграммы, сделанная при вольфрамовом освещении 2700 K CCT и преобразованная в цветовое пространство sRGB для отображения без какой-либо хроматической адаптации. (b) Фотография с балансировкой белого, полученная путем включения CAT для адаптации WP освещения сцены к эталонному белому D65 цветового пространства sRGB.
3.1.
Хроматические адаптационные преобразования
CAT — это вычислительная техника для настройки WP данного SPD. Он достигает этой цели, пытаясь имитировать механизм хроматической адаптации HVS.В контексте цифровых камер наиболее важными CAT являются CAT Брэдфорда и масштабирование необработанных каналов.
В 1902 году фон-Крис постулировал, что механизм хроматической адаптации может быть смоделирован как независимое масштабирование каждой функции отклика конуса глаза, 3 , 4 , что эквивалентно масштабированию трехцветных значений L, M и S. в цветовом пространстве LMS. Чтобы проиллюстрировать CAT фон-Криса, рассмотрите возможность адаптации оценки WP освещения сцены (AW) к WP освещения D65:
Eq.(21)
[XYZ] D65 = CAT_AW → D65 [XYZ] сцена. В этом случае CAT фон Криса, который должен применяться ко всем необработанным векторам пикселей, может быть записан как
Eq. (22)
CAT_AW → D65 = M_vK − 1 [L (D65) L (AW) 000M (D65) M (AW) 000S (D65) S (AW)] M_vK. Матрица M_vK преобразует каждый необработанный вектор пикселей в диагональ матрица в цветовом пространстве LMS. Современные формы M_vK включают матрицы, основанные на основных принципах конуса, определенных CIE в 2006 г. 37 , и матрицу преобразования Ханта – Пойнтера – Эстевеса 38 , определяемую формулой
Eq.(23)
M_vK = [0,389710.68898−0.07868−0.229811.183400.046410.000000.000001.00000]. После применения M_vK значения L, M и S независимо масштабируются в соответствии с гипотезой фон-Криса. В данном примере коэффициенты масштабирования возникают из соотношения между WP AW и D65. Их можно получить из следующих векторов WP:
Eq. (24)
[L (AW) M (AW) S (AW)] = M_vK [X (WP) Y (WP) Z (WP)] сцена [L (D65) M (D65) S (D65)] = M_vK [X (WP) = 0.9504Y (WP) = 1.0000Z (WP) = 1.0888] D65. Наконец, применяется обратная матрица преобразования M_vK для преобразования каждого необработанного вектора пикселей обратно в цветовое пространство CIE XYZ.
Bradford CAT 39 можно рассматривать как улучшенную версию CAT von-Kries. ICC рекомендует упрощенную линеаризованную версию для использования в цифровых изображениях. 40 Линейный КПП Брэдфорда может быть реализован аналогично КАТ фон-Криса, с той разницей, что значения трехцветного стимула L, M и S заменены на ρ, γ и β, которые соответствуют ”Искусственный глазной конус. Матрица преобразования определяется формулой
Eq. (25)
M_BFD = [0.89510.2664-0.1614-0.75021.71350.03670.0389-0.06851.0296].
Аналогично независимому масштабированию функций отклика конуса глаза, предложенному фон-Крисом, тип CAT может применяться в необработанном пространстве камеры путем прямого масштабирования необработанных каналов. Рассмотрим блок Байера для AW, полученный путем фотографирования 100% нейтрального диффузного отражателя при освещении сцены. Следующая операция адаптирует AW к эталонному белому в необработанном пространстве камеры:
Eq. (26)
[RGB] RW = CAT_AW → RW [RGB] сцена, где
Eq.(27)
CAT_AW → RW = D _ = [1R (AW) 0001G (AW) 0001B (AW)] сцена. Коэффициенты масштабирования по диагонали, известные как множители необработанных каналов, могут быть получены непосредственно из исходных данных с использованием AW, рассчитанного с помощью камера. Например, AW = D65 для освещения сцены D65, в этом случае
Eq. (28)
CAT_D65 → RW = D_D65 = [1R (D65) 0001G (D65) 0001B (D65)], где R (D65), G (D65) и B (D65) извлекаются из блока Байера для 100 % нейтральный диффузный отражатель, сфотографированный при освещении сцены D65.
Было обнаружено, что в контексте цифровых камер тип CAT, определяемый множителями необработанных каналов, лучше работает на практике, особенно в крайних случаях. 21 , 32 Причина в том, что множители необработанных каналов применяются в необработанном пространстве камеры до применения матрицы преобразования цвета. Необработанное пространство камеры соответствует физическому устройству захвата, но CAT, такие как линейный CAT Брэдфорда, применяются в цветовом пространстве CIE XYZ после применения матрицы преобразования цвета, содержащей ошибку. В частности, цветовые ошибки, которые были минимизированы в нелинейном цветовом пространстве, таком как CIE LAB, будут неравномерно усилены, поэтому преобразование цвета больше не будет оптимальным. 41
4.
Камеры смартфонов
Производители смартфонов вместе с разработчиками коммерческого программного обеспечения для преобразования необработанных данных обычно реализуют традиционный тип вычислительной стратегии преобразования цвета, используемый в науке о цвете, который был представлен в разд. 3. Поскольку необработанное пространство камеры преобразуется в CIE XYZ в качестве первого шага, методы обработки изображений могут применяться в цветовом пространстве CIE XYZ (или после преобразования в какое-либо другое промежуточное цветовое пространство) перед окончательным преобразованием в ориентированное на вывод Цветовое пространство RGB.
Рассмотрим преобразование с балансировкой белого из необработанного пространства камеры в цветовое пространство RGB, ориентированное на вывод. В отличие от традиционных цифровых камер, цветная демозаика обычно выполняется в первую очередь, поэтому векторная нотация, используемая для необработанного пространства камеры ниже, относится к необработанным векторам пикселей, а не к блокам Байера. В случае sRGB преобразование, которое должно применяться к каждому необработанному вектору пикселей, определяется формулой
Eq. (29)
[RLGLBL] D65 = M_sRGB − 1 CAT_AW → D65 T_ [RGB] сцена.Преобразование можно разбить на три этапа.
1. После того, как камера оценила освещенность сцены WP (AW), применяется матрица характеристик T_, оптимизированная для AW, которая преобразует необработанное пространство камеры в CIE XYZ:
Eq. (30)
[XYZ] scene = T_ [RGB] scene. Оптимизированная матрица T_ обычно нормализуется так, что AW в пространстве CIE XYZ получается, когда необработанный вектор пикселей, соответствующий нейтральному диффузному отражателю, освещенному AW, достигает насыщение:
Ур.(31)
[X (AW) Y (AW) Z (AW)] сцена = T_ [R (AW) G (AW) B (AW)] сцена, где Y (WP) = 1 и макс {R (AW) ), G (AW), B (AW)} = 1. Как обсуждалось в разд. 2.5, зеленый компонент обычно насыщается первым, поэтому R (AW) <1 и B (AW) <1 в целом.
2. Поскольку T_ не изменяет AW, применяется CAT для достижения WB путем адаптации AW к опорному белому в выбранном цветовом пространстве, относящемся к выходу. Это D65 в случае sRGB:
Eq. (32)
[XYZ] D65 = CAT_AW → D65 [XYZ] сцена. ICC рекомендует реализовать CAT, используя линейную матрицу CAT Брэдфорда, определенную уравнением.(25).
3. Применяется матрица, которая преобразует из CIE XYZ в линейную форму выбранного цветового пространства, ориентированного на вывод. В случае sRGB,
Eq. (33)
[RLGLBL] D65 = M_sRGB-1 [XYZ] D65.
Наконец, уровни цифрового вывода выходного изображения определяются путем применения кривой нелинейного гамма-кодирования цветового пространства, указанного на выходе, и уменьшения битовой глубины до 8. В современных цифровых изображениях гамма-кривые кодирования предназначены для минимизации видимых артефакты полос, когда битовая глубина уменьшается, а внесенная нелинейность позже отменяется гаммой дисплея. 28
Чтобы убедиться, что WB достигается правильно, вышеупомянутые шаги могут быть выполнены для конкретного случая необработанного вектора пикселей, который соответствует AW. Как требуется по формуле. (20) было обнаружено, что это отображается на эталонный белый цвет упомянутого на выходе цветового пространства, определенного единичным вектором в этом цветовом пространстве:
[RL = 1GL = 1BL = 1] D65 = M_sRGB − 1 CAT_AW → D65 T_ [R (AW) G (AW) B (AW)] сцена.
Хотя матричное преобразование, определенное формулой. (29) кажется простым, матрица характеристик T_ в принципе должна быть оптимизирована для AW.Однако непрактично определять матрицу характеристик, оптимизированную для каждой возможной WP освещения сцены, которая может возникнуть. Например, если CCT указаны с точностью до ближайшего к Кельвина, а цветовым оттенком пренебрегают, то потребуется 12000 матриц для покрытия WP освещения сцены от 2000 до 14000 K.
Самое простое в вычислительном отношении решение, используемое на некоторых камерах мобильных телефонов, — это приблизить оптимизированная матрица характеристик T_ с использованием единственной фиксированной матрицы, оптимизированной для репрезентативного источника света.Например, это может быть освещение D65, и в этом случае T_, оптимизированное для AW, аппроксимируется как T_D65. Недостатком этого очень простого подхода является то, что преобразование цвета теряет некоторую точность, когда WP освещения сцены значительно отличается от WP репрезентативного источника света.
Как описано ниже, передовым решением проблемы является принятие типа подхода, используемого конвертером Adobe DNG. 32 Идея состоит в том, чтобы интерполировать между двумя предварительно заданными характеристическими матрицами, которые оптимизированы для использования с источником света с низкой или высокой CCT.Для заданного освещения сцены может быть определена интерполированная матрица, оптимизированная для CCT AW.
4.1.
Алгоритм интерполяции
Если используется продвинутый подход, упомянутый выше, оптимизированная матрица характеристик T_, требуемая уравнением. (29) можно вычислить путем интерполяции между двумя характеристическими матрицами T1_ и T2_ на основе оценки CCT освещения сцены, обозначенной CCT (AW), вместе с CCT двух характеризующих осветительных приборов, обозначенных CCT1 и CCT2, соответственно, с CCT1 Первый шаг — надлежащим образом нормализовать T1_ и T2_. Хотя характеристические матрицы обычно нормализуются в соответствии с их соответствующими характеристиками WP осветительных приборов, как показано в разд. 2.5, при реализации алгоритма интерполяции удобнее нормализовать T1_ и T2_ в соответствии с общим WP. К сожалению, на данном этапе невозможно выразить AW с использованием цветового пространства CIE XYZ, поскольку T_ еще предстоит определить.Вместо этого можно выбрать общий WP в качестве эталонного белого цветового пространства, связанного с выводом, то есть D65 для sRGB. В этом случае T1_ и T2_ должны быть масштабированы согласно формуле. (15): [R (WP) G (WP) B (WP)] D65 = T1_ − 1 [X (WP) = 0,9504Y (WP) = 1,0000Z (WP) = 1,0888] D65, [R (WP) G (WP) B (WP)] D65 = T2_ − 1 [X (WP) = 0,9504Y (WP) = 1,0000Z (WP) = 1,0888] D65, где Y (WP) = 1 и max {R (WP) , G (WP), B (WP)} = 1. Если в смартфоне не используется датчик цвета, который может напрямую оценивать WP освещенности сцены с точки зрения координат цветности (x, y), AW рассчитывается камерой в терминах исходных значений R (AW), G (AW) и B (AW), поэтому AW не может быть выражено с использованием цветового пространства CIE XYZ до интерполяции.Однако соответствующий CCT (AW) требует знания координат цветности (x, y), что означает преобразование в CIE XYZ посредством матричного преобразования T_, которое само зависит от неизвестного CCT (AW). Эта проблема может быть решена с помощью самосогласованной итерационной процедуры. 32 1. Сделайте предположение для координат цветности AW, (x (AW), y (AW)). Например, могут использоваться координаты цветности, соответствующие одному из характеризующих осветительных приборов. 2. Найдите значение CCT CCT (AW), которое соответствует координатам цветности (x (AW), y (AW)). Широко используемый подход заключается в преобразовании (x (AW), y (AW)) в соответствующие координаты цветности (u (AW), v (AW)) на диаграмме цветности UCS 1960 года, 23 , 24 где изотермы нормальны к планковскому локусу. Это позволяет определять CCT (AW) с использованием метода Робертсона. 42 В качестве альтернативы могут быть реализованы приблизительные формулы 43 — 45 или более поздние алгоритмы 46 . 3. Выполните интерполяцию так, чтобы T_ (AW) = f [T1_ (CCT1), T2_ (CCT2)], где f — функция интерполяции. Интерполяция действительна, если CCT (AW) 4. Используйте T_ для преобразования AW из необработанного пространства камеры в цветовое пространство CIE XYZ: [X (AW) Y (AW) Z (AW)] сцена = T_ [R (AW) G (AW) B (AW)] сцена. Это дает новое предположение для (x (AW), y (AW)). 5. Повторяйте процедуру, начиная с шага 2, до тех пор, пока (x (AW), y (AW)), CCT (AW) и T_ все не сойдутся к стабильному решению. После того, как интерполяция была выполнена, T_ наследует нормализацию уравнения. (34). Однако теперь AW может быть выражено с использованием цветового пространства CIE XYZ, поэтому T_ можно перенормировать, чтобы удовлетворить уравнению. (31). Если в смартфоне используется датчик цвета, который может напрямую оценивать WP освещенности сцены с точки зрения координат цветности (x, y), то требуются только шаги 2 и 3, указанные выше. Рассмотрим снова сбалансированное по белому преобразование из необработанного пространства камеры в цветовое пространство RGB, ориентированное на вывод. В случае sRGB преобразование определяется формулой. (29): [RLGLBL] D65 = M_sRGB − 1 CAT_AW → D65 T_ [RGB] сцена, где CAT_AW → D65 адаптирует оценку WP освещения сцены (AW) к эталонному белому цветовому пространству sRGB D65. Традиционные производители камер обычно переформулируют приведенное выше уравнение следующим образом: [RLGLBL] D65 = R_D_ [RGB] сцена. Это уравнение можно интерпретировать, разложив преобразование на два этапа. 1. Матрица D_ — это диагональная матрица баланса белого, содержащая необработанные множители каналов, подходящие для AW: D _ = [1R (AW) 0001G (AW) 0001B (AW)] сцена. Они применяются к необработанным каналам перед цветной демозаикой. Как показано формулой. (27), множители необработанного канала, в частности, служат для хроматической адаптации AW к эталонному белому необработанному пространству камеры: [R = 1G = 1B = 1] ссылка = сцена D_ [R (AW) G (AW) B (AW)]. 2. Матрица R_ — это матрица поворота цвета, оптимизированная для освещения сцены. После выполнения цветовой демозаики применяется R_ для преобразования непосредственно из необработанного пространства камеры в линейную форму выбранного цветового пространства, ориентированного на вывод. По сравнению с уравнениями. (29) и (37), R_ алгебраически определяется как R_ = M_sRGB − 1 CAT_AW → D65 T_ D_ − 1. Матрицы поворота цвета обладают тем важным свойством, что каждая из их строк суммируется до единицы: R (1,1) + R (1,2) + R (1,3) = 1, R (2,1) + R (2,2) + R (2,3) = 1, R (3,1) + R (3,2) + R (3,3) = 1. Следовательно, R_ сопоставляет эталонный белый цвет необработанного пространства камеры непосредственно с эталонным белым цветовым пространством, указанным на выходе. 21 В случае sRGB [RL = 1GL = 1BL = 1] D65 = R_ [R = 1G = 1B = 1] эталон. Объединение уравнений. (39) и (42) показывают, что общий WB достигается, поскольку необработанный вектор пикселей, соответствующий AW, отображается на опорный белый цвет упомянутого на выходе цветового пространства: [RL = 1GL = 1BL = 1] D65 = R_D_ [R (AW) G (AW) B (AW)] сцена. Как и характеристическая матрица T_, матрица поворота цвета R_ в принципе должна быть оптимизирована для освещения сцены. Вместо того, чтобы использовать подход, основанный на интерполяции, переформулировка в форме уравнения. (37) позволяет традиционным производителям камер принять альтернативный и простой в вычислительном отношении подход, который может быть напрямую реализован на архитектуре с фиксированной точкой. Хотя уравнение.(37) кажется простой переформулировкой уравнения. (29), он имеет несколько преимуществ, которые возникают из-за извлечения необработанных множителей канала, содержащихся в матрице D_ ББ. Как показано на фиг. 8, изменение элементов матрицы поворота цвета относительно CCT очень мало. Стабильность выше, чем у элементов обычной характеристической матрицы T_, как видно из сравнения фиг. 5 и 8. Изменение элементов матрицы матрицы вращения R_ raw-to-sRGB, используемой камерой Olympus E-M1, в зависимости от CCT. Следовательно, достаточно определить небольшой набор из n предварительно установленных матриц поворота цветов, которые покрывают диапазон WP или CCT, причем каждая матрица оптимизирована для конкретной предварительно установленной WP или CCT: R_i = M_sRGB − 1 CAT_AW → D65 T_i D_i − 1, где i = 1… n. Когда AW рассчитывается камерой, может быть выбрана матрица поворота цвета R_i, оптимизированная для наиболее подходящей предустановки WP или CCT. Однако матрица WB D_, соответствующая AW, всегда применяется до R_i, поэтому полное преобразование цвета может быть выражено как [RLGLBL] D65 = (M_sRGB − 1 CAT_AW → D65 T_i D_i − 1) D_ [RGB] сцена. Поскольку D_ отделен от матриц вращения, этот подход позволит добиться правильного баланса белого без необходимости интерполировать матрицы вращения. . Следует отметить, что необработанное пространство камеры правильно представляет сцену (хотя и с помощью нестандартной цветовой модели) и что множители необработанного канала, содержащиеся в D_, не применяются для «исправления» чего-либо, касающегося представления истинного белого цвета сцены с помощью необработанное пространство камеры, как это часто предполагается.Множители применяются для хроматической адаптации AW к эталонному белому в необработанном пространстве камеры как часть общей CAT, необходимой для достижения WB, путем имитации механизма хроматической адаптации HVS. Как показано на рис.4, эталонный белый цвет необработанного пространства камеры обычно является пурпурным цветом при использовании колориметрии CIE, но он служит полезным промежуточным этапом в требуемом преобразовании цвета, поскольку он облегчает выделение компонента масштабирования канала, который можно отделить от матричной операции.К другим преимуществам переформулировки можно отнести следующее. • Множители сырых каналов, содержащиеся в D_, могут быть применены к необработанным каналам до выполнения цветной мозаики. В результате получается демозаика лучшего качества. 21 • Метод может быть эффективно реализован в архитектуре с фиксированной точкой. 47 • При желании, часть масштабирования необработанного канала может быть выполнена в аналоговой области с использованием аналогового усиления.Это полезно для качества изображения, если аналого-цифровой преобразователь (АЦП) не имеет достаточно высокой битовой глубины. Обратите внимание, что этот тип аналогового усиления будет влиять на коэффициенты преобразования единицы измерения gi, относящиеся к входу и выходу, определенные уравнением. (80) в Приложении. • Необработанные множители каналов, содержащиеся в D_, которые появляются в уравнении. (37) хранятся в метаданных проприетарных необработанных файлов и применяются внутренним механизмом обработки изображений JPEG камеры. Поскольку множители необработанных каналов не влияют на необработанные данные, они могут использоваться внешним программным обеспечением для преобразования необработанных данных, предоставляемым производителем камеры, и могут быть легко настроены пользователем. • Предварительные настройки освещения сцены, которые включают в себя цветовой оттенок, могут быть напрямую реализованы путем сохранения соответствующих предварительно установленных матриц поворота цветов и множителей необработанных каналов, как показано в разд. 5.2. Хотя цветовые матрицы, используемые производителями камер, как правило, неизвестны, некоторые производители, такие как Sony и Olympus, раскрывают информацию о матрицах поворота цвета, используемых их камерами, которую можно извлечь из необработанных метаданных. . В таблице 1 перечислены данные, показанные на рис. 8, для предварительно установленных матриц поворота цвета, используемых цифровой камерой Olympus E-M1, а также диапазоны CCT освещения сцены, в которых применяется каждая матрица. На рисунке 9 показано, как множители необработанных каналов для одной и той же камеры меняются в зависимости от CCT. Данные были извлечены из необработанных метаданных с помощью бесплатного приложения ExifTool. 48 Стратегию преобразования цвета камеры можно резюмировать следующим образом. 1.Камера определяет оценку WP освещения сцены (AW), используя алгоритм автоматического баланса белого, выбранную предустановку освещения сцены или настраиваемую CCT, предоставленную пользователем. AW используется для расчета соответствующих множителей необработанных каналов с помощью уравнения. (38) так, чтобы диагональная матрица WB D_ могла быть применена к необработанным каналам. В частности, D_ служит для адаптации AW к эталонному белому в необработанном пространстве камеры. 2. После выполнения цветовой демозаики камера выбирает предварительно установленную матрицу поворота цвета R_i, оптимизированную для освещения с помощью CCT, которая обеспечивает наиболее близкое соответствие CCT, связанного с AW, или наиболее близкую предустановку освещения сцены. 3. Камера применяет R_i для преобразования в цветовое пространство с привязкой к выходу, выбранное пользователем в камере, например sRGB. В частности, эталонный белый цвет необработанного пространства камеры отображается на эталонный белый цвет выбранного цветового пространства, ориентированного на вывод, которым является D65 в случае sRGB. Камера Olympus E-M1 также включает несколько предустановок освещения сцены. Матрицы поворота цвета и соответствующие множители необработанных каналов для этих предустановок сцены перечислены в таблице 2.Обратите внимание на то, что для заданного CCT предварительно заданные матрицы и множители сцены не обязательно совпадают с теми, что перечислены в таблице 1. Это связано с тем, что визуализации предварительно заданных сцен включают цветовой оттенок вдали от планковского локуса, поэтому координаты цветности не обязательно являются такие же, как перечисленные в таблице 1 для данной CCT. По той же причине обратите внимание, что предустановки сюжетных режимов «хорошая погода», «под водой» и «вспышка» фактически используют одну и ту же матрицу поворота цвета, но используют очень разные множители необработанных каналов. Матрицы поворота цвета Raw-to-sRGB, соответствующие диапазонам настраиваемых CCT в камере для камеры Olympus E-M1 с объективом 12-100 / 4 и прошивкой v4.1. В среднем столбце перечислены матрицы, извлеченные из необработанных метаданных, которые представляют собой 8-битные числа с фиксированной запятой. При делении на 256 в правом столбце отображаются одни и те же матрицы с четырьмя десятичными знаками, так что сумма каждой строки равна единице, а не 256. Множители необработанных каналов, используемые камерой Olympus E-M1, как функция CCT. Камера использует одинаковые множители для обоих зеленых каналов. Матрицы поворота цвета Raw-to-sRGB и соответствующие множители необработанных каналов, соответствующие режимам сцены в камере для камеры Olympus E-M1 с объективом 12-100 / 4 и v4.1 прошивка. Все значения представляют собой 8-битные числа с фиксированной запятой, которые можно разделить на 256. Поскольку предустановки режима сцены включают цветовой оттенок вдали от планковского локуса, множители и матрицы не обязательно имеют те же значения, что и пользовательские предустановки CCT с тот же CCT, указанный в таблице 1. 10000 Для любой данной модели камеры все предустановленные матрицы поворота цвета зависят от таких факторов, как цветовое пространство на выходе, выбранное пользователь в настройках камеры (например, sRGB или Adobe ® RGB), модель объектива, с которой был сделан снимок, и версия прошивки.Из-за различий в калибровке датчиков между разными примерами одной и той же модели камеры также может быть зависимость от отдельной камеры, используемой для съемки. Например, на рис. 10 (а) показана фотография цветовой диаграммы в необработанном пространстве камеры, сделанная при освещении D65. Как и на рис. 6 (a), оттенок зеленого цвета возникает из-за того, что значения RGB необработанного пространства камеры интерпретируются как значения RGB в цветовом пространстве sRGB для целей отображения без применения какой-либо матрицы цветовых характеристик для преобразования цветов.На рисунке 10 (b) показана та же фотография после применения диагональной матрицы баланса белого D_ для хроматической адаптации AW к исходному белому пространству камеры. Множители необработанных каналов удаляют зеленый оттенок, но фотография остается в необработанном пространстве камеры. Примечательно, что цвета кажутся реалистичными, хотя и ненасыщенными. Чтобы проиллюстрировать, что эталонный белый цвет необработанного пространства камеры на самом деле является пурпурным цветом при использовании колориметрии CIE, рис.10 (c) преобразует (b) в цветовое пространство sRGB без какой-либо дальнейшей хроматической адаптации путем применения стандартной матрицы характеристик T_, за которой следует M_sRGB. −1.Напротив, рис. 10 (d) был получен путем применения соответствующих умножителей необработанных каналов, за которыми следовала матрица поворота цветов sRGB R_ вместо T_ и M_sRGB-1. Матрица поворота цвета включает в себя CAT, который адаптирует эталонный белый цвет необработанного пространства камеры к эталонному белому цветовому пространству sRGB D65. В этом конкретном случае D_ = D_D65, поэтому матрица поворота цвета R_, определенная формулой. (40) становится R_≡R_D65 = M_sRGB − 1 T_D65 D_D65-1. Подставляя в уравнение. (37) дает [RLGLBL] D65 = M_sRGB-1 T_D65 D_D65-1 D_D65 [RGB] сцена. Следовательно, матрица вращения обращает эффект матрицы WB, поскольку освещение сцены и дисплея одинаковое. (a) Фотография цветовой диаграммы в необработанном пространстве камеры, сделанная при освещении D65. (b) После применения соответствующих коэффициентов необработанных каналов. Они удаляют зеленый оттенок, но фотография остается в необработанном пространстве камеры. (c) После применения соответствующих умножителей необработанных каналов и преобразования в sRGB без какой-либо дальнейшей хроматической адаптации.Белый участок показывает истинный цвет эталонного белого космического пространства камеры. (d) После применения соответствующих умножителей необработанных каналов и матрицы поворота цветов sRGB R_. Широко используемый преобразователь RAW с открытым исходным кодом DCRaw (произносится как «dee-see-raw»), написанный Д. Коффином, может обрабатывать большое количество форматов необработанных файлов изображений. Он особенно полезен для научного анализа, поскольку он может декодировать необработанные файлы без демозаики, он может применять линейные кривые тона и может напрямую выводить в необработанное пространство камеры и цветовое пространство CIE XYZ.Некоторые соответствующие команды перечислены в таблице 3. Однако DCRaw по умолчанию выводит непосредственно в цветовое пространство sRGB с WP подсветкой D65, используя вариант традиционной стратегии цифровой камеры, описанной в предыдущем разделе. 28 Напомним, что матрица вращения цвета, оптимизированная для использования с освещением сцены, определяется формулой. (40): R_ = M_sRGB − 1 CAT_AW → D65 T_ D_ − 1. Хотя цифровые камеры обычно используют небольшой набор предустановленных матриц поворота, оптимизированных для выбора предустановленных источников света, DCRaw вместо этого использует очень простой в вычислительном отношении подход, который использует только матрица одиночного вращения, оптимизированная для освещения сцены D65, R_≈R_D65.Это достигается с помощью характеристической матрицы T_D65, оптимизированной для освещения D65, что означает, что матрица D_-1, содержащаяся в R_, заменяется на D_D65-1, и матрица CAT_AW → D65 не требуется: R_D65 = M_sRGB-1 T_D65 D_D65-1. Диагональная матрица баланса белого D_D65 содержит множители сырых каналов, подходящие для освещения D65: D_D65 = [1R (WP) 0001G (WP) 0001B (WP)] D65 = [1R (D65) 0001G (D65) 0001B (D65)]. Общее преобразование из необработанного пространства камеры в линейную форму sRGB определяется формулой [RLGLBL] D65≈R_D65 D_ [RGB] сцена, которую можно более явно записать как [RLGLBL] D65≈M_sRGB − 1 T_D65 [R (D65) R (AW) 000G (D65) G (AW) 000B (D65) B (AW)] [RGB] сцена. Следовательно, вся хроматическая адаптация выполняется выполняется с использованием множителей сырых каналов. Обратите внимание, что матрица WB D_, соответствующая оценке освещенности сцены, всегда применяется к необработанным данным в формуле. (50), поэтому WB всегда в принципе достигается правильно. Выбор соответствующих команд DCraw, доступных в версии 9.28. Обратите внимание, что параметры цветового пространства вывода RGB используют матрицы поворота цветов и поэтому должны использоваться только с правильными множителями сырых каналов из-за встроенного CAT. Хотя матрица преобразования цвета T_D65 оптимизирована для освещения сцены D65, Применение матрицы поворота цвета R_D65 для преобразования из необработанного пространства камеры в sRGB допустимо для любого CCT освещения сцены, поскольку матрицы поворота цвета изменяются очень медленно в зависимости от CCT, как видно из рис.8. Однако R_D65 является оптимальным выбором для освещения сцены D65, поэтому недостатком этого упрощенного подхода является то, что общее преобразование цвета теряет некоторую точность, когда освещение сцены значительно отличается от D65. DCRaw использует матрицы поворота цвета, полученные с помощью уравнения. (48), поэтому для данной модели камеры требуется матрица характеристик T_D65. Для этой цели DCRaw использует матрицы Adobe «ColorMatrix2» из конвертера Adobe ® DNG. 32 Из-за требований к логике восстановления, матрицы Adobe отображаются в противоположном направлении по отношению к традиционным матрицам характеристик, определенным в разд. 2.4, и, следовательно, T_D65 = (1cColorMatrix2 _) — 1, где c — нормировочная константа. Для цифровой камеры Olympus E-M1 исходный код DCRaw хранит записи ColorMatrix2 следующим образом: 7687, −1984, −606, −4327, 11928, 2721, −1381, 2339, 6452. Деление на 10000 и преобразование в матричная форма дает ColorMatrix2 _ = [0,7687-0,1984-0,0606-0,43271,19280.2721-0,13810,23390,6452]. Вызов из разд. 2.5 следует, что характеристические матрицы обычно нормализуются таким образом, что WP характеристического источника света отображается на необработанные значения, так что максимальное значение (обычно зеленый канал) просто достигает насыщения, когда 100% нейтральный диффузный отражатель фотографируется под характеристическим источником света. Хотя матрицы ColorMatrix2 оптимизированы для освещения CIE D65, они по умолчанию нормализованы в соответствии с WP осветителя CIE D50, а не D65: [R (WP) G (WP) B (WP)] D50 = ColorMatrix2_ [X (WP) = 0,9642Y (WP) = 1,0000Z (WP) = 0,8249] D50, где max {R (WP) , G (WP), B (WP)} = 1. Соответственно, их необходимо масштабировать для использования с DCRaw: [R (WP) G (WP) B (WP)] D65 = 1cColorMatrix2_ [X (WP) = 0.9504Y (WP) = 1.0000Z (WP) = 1.0888] D65, где max {R (WP) , G (WP), B (WP)} = 1. В данном примере найдено, что c = 1,0778, поэтому T_D65-1 = [0,7133-0,1841-0,0562-0,40151,10680,2525-0,12810,21700,5987]. С учетом единичного вектора в цветовом пространстве sRGB указанная выше матрица может использоваться для получения необработанных значений трехцветного изображения для D65. освещение WP: [R (WP) = 0,4325G (WP) = 1,0000B (WP) = 0,7471] D65 = T_D65−1 M_sRGB [RL = 1GL = 1BL = 1] D65, где M_sRGB преобразуется из линейной формы sRGB. в CIE XYZ. Теперь уравнение. (49) можно использовать для извлечения множителей сырых каналов для освещения сцены с помощью D65 WP: D_D65 = [2.311700010001.3385]. Наконец, матрица вращения цвета может быть рассчитана по формуле. (48): R_D65 = [1,7901-0,6689-0,1212-0,21671,7521-0,53540,0543-0,55821,5039]. Сумма в каждой строке при необходимости сводится к единице. Форма матрицы аналогична встроенным в камеру матрицам Olympus, перечисленным в таблице 1.Для целей сравнения соответствующая приведенная матрица является той, которая действительна для CCT источников света сцены в диапазоне от 5800 до 6600 K. Ожидаются некоторые численные различия, поскольку освещение D65 имеет цветовой оттенок Duv = 0,0032. Другие численные различия, вероятно, связаны с разницей в методах характеризации Olympus и Adobe. Кроме того, Adobe использует таблицы HSV (оттенок, насыщенность и значение) для имитации окончательной цветопередачи встроенного в камеру механизма обработки JPEG. Как показано в таблице 3, DCRaw включает множество команд, которые полезны для научных исследований.Однако важно отметить, что параметры цветового пространства вывода RGB используют матрицы поворота цвета, а не конкатенацию необработанных матриц с CIE XYZ и CIE XYZ с матрицами RGB. Поскольку матрицы поворота цвета включают встроенный CAT, эти параметры позволят достичь ожидаемого результата только в сочетании с правильными множителями необработанных каналов. Например, установка множителя каждого необработанного канала на единицу не предотвратит выполнение некоторой частичной хроматической адаптации, если выбран выход sRGB, поскольку матрица вращения цвета DCRaw включает в себя матрицу D_D65-1, которая является типом CAT_RW → D65. Надежным способом использования DCRaw для научных исследований является команда «dcraw -v -D -4 -T filename», которая обеспечивает линейный 16-битный вывод TIFF в необработанном цветовом пространстве без балансировки белого, демозаики или преобразования цвета. . Последующая обработка может быть выполнена после импорта файла TIFF в MATLAB ® с использованием обычной команды «imread». Ссылка 49 предоставляет учебное пособие по обработке. Цветные диаграммы фотографий в данной статье были получены с использованием этой методики. Например, после импорта файла в MATLAB с помощью приведенных выше команд видимое выходное изображение в цветовом пространстве sRGB без какой-либо балансировки белого может быть получено путем применения соответствующей матрицы характеристик T_ после цветовой демозаики с последующим прямым применением стандартная матрица CIE XYZ в sRGB, M_sRGB − 1. Adobe ® DNG — это формат необработанных файлов с открытым исходным кодом, разработанный Adobe. 32 , 50 Бесплатная программа DNG Converter может быть использована для преобразования любого необработанного файла в формат DNG. Хотя конвертер DNG не нацелен на создание видимого выходного изображения, он выполняет преобразование цвета из необработанного пространства камеры в пространство соединения профиля (PCS) на основе цветового пространства CIE XYZ с освещением D50 WP. 40 (Это не фактический эталонный белый цвет CIE XYZ, который является источником света CIE E.) Следовательно, модель обработки цвета, используемая конвертером DNG, должна обеспечивать соответствующие матрицы характеристик вместе со стратегией для достижения правильного баланса белого по отношению к Шт.При обработке файлов DNG необработанные преобразователи могут напрямую отображать из PCS в любое выбранное цветовое пространство, указанное на выходе, и связанный с ним эталонный белый цвет. Спецификация DNG предоставляет две разные модели обработки цвета, называемые здесь методом 1 и методом 2. Метод 1 использует ту же стратегию, что и смартфоны и коммерческие преобразователи необработанных данных, с той разницей, что данные остаются в PCS. Метод 2, использующий умножители необработанных каналов, использует ту же стратегию, что и традиционные цифровые камеры.Однако множители применяются вместе с так называемой прямой матрицей вместо матрицы вращения, поскольку отображение выполняется на PCS, а не на цветовое пространство RGB, относящееся к выходу. Преобразование из необработанного пространства камеры в PCS определяется следующим образом: [XYZ] D50 = CAT_AW → D50 C_ − 1 [RGB] сцена. Здесь C_ — это цветовая матрица Adobe, оптимизированная для сцены AW. Из-за требований логики восстановления выделения, цветовые матрицы Adobe отображаются в направлении от цветового пространства CIE XYZ до необработанного пространства камеры: [RGB] scene = C_ [XYZ] scene. Это направление противоположно традиционной матрице характеристик T_, поэтому после обратного преобразования C_ из необработанного пространства камеры в CIE XYZ для адаптации применяется линейный Брэдфордский CAT AW к WP PCS. Аналогично проблеме, описанной в гл. 4 для смартфонов, реализация уравнения. (60) усложняется тем, что C_ следует оптимизировать для сцены AW. Оптимизированная матрица C_ определяется путем интерполяции между двумя цветовыми матрицами, обозначенными ColorMatrix1 и ColorMatrix2, где ColorMatrix1 должен быть получен из характеристики, выполненной с использованием источника света с низким CCT, такого как источник света CIE A, и ColorMatrix2 должен быть получен из характеристики, выполненной с использованием высокого Источник света CCT, такой как осветитель CIE D65. 32 Оптимизированная матрица C_ вычисляется путем интерполяции между ColorMatrix1 и ColorMatrix2 на основе оценки CCT освещения сцены, обозначенной CCT (AW), вместе с CCT, связанных с каждым из двух характеризующих источников света, обозначенных CCT1 и CCT2, соответственно. , с CCT1 Вызов из разд. 2.5, что характеристические матрицы обычно нормализованы так, что характеризующий источник света WP в цветовом пространстве CIE XYZ просто насыщает необработанные данные в необработанном пространстве камеры и что зеленый необработанный канал обычно насыщается первым.Однако в данном контексте матрицы Adobe ColorMatrix1 и ColorMatrix2 требуют общей нормализации, которая удобна для выполнения интерполяции. Аналогично разд. 4.1 AW неизвестен в терминах цветового пространства CIE XYZ до интерполяции. Вместо этого ColorMatrix1 и ColorMatrix2 по умолчанию нормализованы, так что WP PCS просто насыщает необработанные данные: [R (WP) G (WP) B (WP)] D50 = ColorMatrix1_ [X (WP) = 0,9642Y (WP) = 1,0000Z (WP) = 0,8249] D50, [R (WP) G ( WP) B (WP)] D50 = ColorMatrix2_ [X (WP) = 0.9642Y (WP) = 1,0000Z (WP) = 0,8249] D50, где max {R (WP), G (WP), B (WP)} = 1. Например, значения по умолчанию ColorMatrix1 и ColorMatrix2 для камеры Olympus E-M1, соответственно, нормализованы следующим образом: [R (WP) = 0,5471G (WP) = 1,0000B (WP) = 0,6560] D50 = [1,1528-0,57420,0118-0,24531,02050,2619-0,07510,1890,6539] [X (WP) = 0,9642Y ( WP) = 1,0000Z (WP) = 0,8249] D50, [R (WP) = 0,4928G (WP) = 1,0000B (WP) = 0,6330] D50 = [0,7687-0,1984-0,0606-0,43271,19280,2721-0,13810,23390,6452] [X (WP) = 0,9642Y (WP) = 1,0000Z (WP) = 0,8249] D50. Интерполированный C_ изначально наследует эту нормализацию.Однако после определения C_ значения CIE XYZ для AW будут известны. Следовательно, исходный код Adobe DNG SDK позже повторно нормализует Eq. (60), так что AW в необработанном пространстве камеры отображается на WP PCS, когда необработанные данные просто насыщаются: [X (WP) = 0.9641Y (WP) = 1.0000Z (WP) = 0.8249] D50 = CAT_AW → D50 C_ − 1 [R (AW) G (AW) B (AW)] сцена, где макс. {R (WP), G (WP), B (WP)} = 1. Это эквивалентно перенормировке C_ следующим образом: [R (AW) G (AW) B (AW)] сцена = C_ [X (AW) Y (AW) Z (AW)] сцена, где Y (AW) = 1 и max {R (WP ), G (WP), B (WP)} = 1. Алгоритм интерполяции метода 1 такой же, как описанный в разд. 4.1, за исключением того, что ColorMatrix1, ColorMatrix2 и C_ заменяют T1_, T2_ и T_ соответственно. Кроме того, спецификация Adobe DNG требует, чтобы метод интерполяции был линейной интерполяцией на основе обратной CCT. 32 Опять же, сама интерполяция усложняется тем фактом, что AW обычно рассчитывается камерой в терминах необработанных значений R (AW), G (AW) и B (AW), но соответствующие CCT ( AW) требует знания координат цветности (x, y).Это означает преобразование в CIE XYZ с помощью матричного преобразования C_, которое само зависит от неизвестного CCT (AW), которое может быть решено с помощью процедуры самосогласованного итерационного анализа. 1. Сделайте предположение для координат цветности AW, (x (AW), y (AW)). Например, могут использоваться координаты цветности, соответствующие одному из характеризующих осветительных приборов. 2. Найдите значение CCT CCT (AW), которое соответствует координатам цветности (x (AW), y (AW)), используя один из методов, перечисленных в шаге 2 разд.4.1. 3. Выполните линейную интерполяцию: C_ = α ColorMatrix1 _ + (1 − α) ColorMatrix2_, где α — зависимое от CCT взвешивание, которое зависит от обратного CCT: α = (CCT (AW)) — 1− (CCT2) −1 (CCT1) −1− (CCT2) −1. Эти веса (обозначены g и 1 − g в исходном коде Adobe DNG SDK) проиллюстрированы на рис. 11 для пары примерных значений CCT1 и CCT2. Интерполяция действительна для CCT (1) ≤CCT (AW) ≤CCT (2). Если CCT (AW) 4. Используйте C_ для преобразования AW из необработанного пространства камеры в CIE XYZ: [X (AW) Y (AW) Z (AW)] сцена = C_ − 1 [R (AW) G (AW) B (AW)] сцена. Это дает новое предположение для (x (AW) , y (AW)). 5. Повторяйте процедуру, начиная с шага 2, пока (x (AW), y (AW)), CCT (AW) и C_ все не сойдутся к стабильному решению. 6. Нормализуйте преобразование цвета в соответствии с формулой. (65). На рисунке 12 показаны результаты линейной интерполяции на основе обратной CCT с использованием цветовых матриц Adobe, определенных формулой.(64) для камеры Olympus E-M1. Обратите внимание, что ColorMatrix2 такая же, как определенная формулой. (53), который был извлечен из исходного кода DCRaw. Весовые коэффициенты линейной интерполяции α и 1 − α на основе обратной CCT с CCT1 = 2855 K и CCT2 = 6504 K. Оптимизированная цветовая матрица C_, построенная как функция CCT и полученные с помощью линейной интерполяции на основе обратной CCT матриц преобразования цвета Adobe ColorMatrix1 (источник света A, CCT2 = 2855 K) и ColorMatrix2 (источник света D65, CCT2 = 6504 K) для камеры Olympus E-M1. Поскольку C_ отображается в направлении от цветового пространства CIE XYZ к необработанному пространству камеры, инверсию интерполированного C_ можно сравнить с традиционной характеристической матрицей T_ при заданном CCT источника света. На рисунке 13 показан график, обратный интерполированному C_ как функция CCT, и этот рисунок можно сравнить с рисунком 5, на котором показаны стандартные матрицы характеристик для той же камеры, оптимизированные для выбора CCT. Хотя на этих двух графиках используются разные нормализации, поскольку характеристические матрицы нормализованы в соответствии с их характеристическим источником света WP, а не WP PCS, вариации относительно CCT аналогичны.Однако очевидно, что интерполированный C_ теряет точность для CCT ниже CCT1. Инверсия интерполированной цветовой матрицы C_, представленной на рис. 12. Рассмотрим преобразование из необработанного пространства камеры в PCS, определенное уравнением. (60): [XYZ] D50 = CAT_AW → D50 C_ − 1 [RGB] сцена, где C_ — это цветовая матрица Adobe, оптимизированная для сцены AW. Метод 2 переформулирует вышеуказанное преобразование следующим образом: [XYZ] D50 = F_D_ [RGB] сцена. Преобразование цвета можно разделить на два этапа. 1. Аналогично стратегии преобразования цвета традиционных цифровых фотоаппаратов, описанной в разд. 5 диагональная матрица D_, определенная формулой. (38) содержит множители необработанных каналов, подходящие для AW, т. Е. Оценочную оценку WP освещения сцены: D _ = [1R (AW) 0001G (AW) 0001B (AW)] сцена. В частности, множители необработанных каналов служат для хроматической адаптировать AW к эталонному белому цвету необработанного пространства камеры: [R = 1G = 1B = 1] = D_ [R (AW) G (AW) B (AW)] сцена. Обратите внимание, что спецификация Adobe DNG также учитывает необработанные множители каналов, применяемые в аналоговой области. 32 Однако в последних цифровых камерах используются АЦП с относительно высокой битовой глубиной порядка 12 или 14, и, следовательно, в цифровой области используются умножители необработанных каналов. 2. Прямая матрица F_ — это тип характеристической матрицы, которая отображает необработанное пространство камеры в PCS и оптимизирована для освещения сцены.Поскольку PCS основана на цветовом пространстве CIE XYZ с WP освещенности D50, передняя матрица F_ включает в себя встроенную CAT, поскольку она также должна адаптировать эталонный белый необработанного пространства камеры к WP освещения D50: [X (WP) = 0,9642Y (WP) = 1,0000Z (WP) = 0,8249] D50 = F_ [R = 1G = 1B = 1]. Поскольку прямая матрица F_ должна быть оптимизирована для сцены AW, на практике она определяется интерполяцией между двумя прямыми матрицами аналогично подходу интерполяции, используемому в методе 1.Спецификация Adobe DNG предоставляет теги для двух прямых матриц, обозначенных ForwardMatrix1 и ForwardMatrix2, которые должны снова быть получены из характеристик, выполненных с использованием источника света с низким CCT и источника света с высоким CCT, соответственно. Следует использовать тот же метод интерполяции, который описан в предыдущем разделе, с ForwardMatrix1, ForwardMatrix2 и F_ вместо ColorMatrix1, ColorMatrix2 и C_, соответственно, F_ = α ForwardMatrix1 _ + (1 − α) ForwardMatrix2_. На рисунке 14 показана оптимизированная прямая матрица, интерполированная из ForwardMatrix1 и ForwardMatrix2 и выраженная как функция CCT для камеры Olympus E-M1. Оптимизированная прямая матрица F_, построенная как функция CCT и полученная с помощью линейной интерполяции на основе обратной CCT матрицы Adobe ForwardMatrix1 (источник света A, CCT2 = 2855 K) и прямой матрицы 2 (источник света D65, CCT2 = 6504 K ) матрицы для фотоаппарата Olympus E-M1. Очевидно, что элементы оптимизированной прямой матрицы F_ изменяются очень медленно и стабильно как функция CCT, аналогично элементам матрицы поворота цвета, показанным на рис. 8. Путем сравнения формул.(60) и (70), F_ алгебраически связана с цветовой матрицей C_ следующим образом: F_ = CAT_AW → D50 C_ − 1 D_ − 1. Поскольку на практике F_ интерполируется из ForwardMatrix1 и ForwardMatrix2, они определяются как ForwardMatrix1_ = CAT_AW → D50 ColorMatrix1_ − 1 D_ − 1ForwardMatrix2_ = CAT_AW → D50 ColorMatrix2_ − 1 D_ − 1 Согласно уравнению. (72) оптимизированная прямая матрица F_ по определению нормализована так, что единичный вектор в необработанном пространстве камеры отображается на WP D50 PCS. 32 Это означает, что ForwardMatrix1 и ForwardMatrix2 также должны быть нормализованы таким образом. Например, значения по умолчанию ForwardMatrix1 и ForwardMatrix2 для камеры Olympus E-M1, соответственно, нормализованы следующим образом: [X (WP) = 0,9643Y (WP) = 0,9999Z (WP) = 0,8251] D50 = [0,47340,36180,12910,27650,68270.04070,21160,00060,6129] [R = 1G = 1B = 1], [X ( WP) = 0.9643Y (WP) = 1.0000Z (WP) = 0.8252] D50 = [0.46330.32440.17660.27790.66610.05600.17220.00330.6497] [R = 1G = 1B = 1]. Официальный WP D50 PCS на самом деле X = 0.9642, Y = 1,0000 и Z = 0,8249, 40 , что является 16-битным дробным приближением истинного WP D50, определяемого как X = 0,9642, Y = 1,0000 и Z = 0,8251. В первом разделе этой статьи показано, как RAW-конвертер с открытым исходным кодом DCRaw можно использовать для непосредственного определения характеристик камеры без необходимости определять и инвертировать OECF, а также показано, как матрицы характеристик нормализуются на практике. Как следствие метамерной ошибки камеры, необработанное пространство камеры для типичной камеры оказалось деформированным от треугольной формы, доступной для аддитивных линейных комбинаций трех фиксированных основных цветов на диаграмме цветности xy, а доступная гамма оказалась зависимой. по характеристике осветительного прибора.Также было показано, что эталонный белый цвет типичного необработанного пространства камеры имеет сильный пурпурный оттенок. Впоследствии в этой статье были исследованы и сопоставлены типы стратегий преобразования цвета, используемые камерами смартфонов и коммерческими преобразователями RAW, механизмами обработки изображений традиционных цифровых камер, DCRaw и преобразователем Adobe DNG. Смартфоны и приложения для преобразования необработанных данных обычно используют стратегию преобразования цвета, знакомую в науке о цвете.Это включает в себя применение матрицы характеристик T_ для преобразования из необработанного пространства камеры в цветовое пространство CIE XYZ, CAT для хроматической адаптации оцененного WP освещения сцены к эталонному белому цветового пространства, упомянутого на выходе (например, D65 для sRGB), и, наконец, преобразование из CIE XYZ в линейную форму выбранного цветового пространства, ориентированного на вывод. Поскольку оптимизированная матрица характеристик зависит от CCT, если не выполняется условие Лютера-Айвза, оптимизированная матрица может быть определена путем интерполяции между двумя предварительно установленными характеристическими матрицами, одна оптимизирована для источника света с низкой CCT, а другая оптимизирована для источника света с высокой CCT. .Более простые решения включают использование фиксированной матрицы характеристик, оптимизированной для репрезентативного освещения сцены. Для традиционных цифровых камер в этой статье показано, как общее преобразование цвета обычно переформулируется в терминах множителей сырых каналов D_ вместе с набором матриц поворота цветов R_. Множители необработанных каналов действуют как тип CAT, хроматически адаптируя оценку WP освещения сцены к эталонному белому необработанного пространства камеры. Поскольку каждая строка матрицы поворота цвета равна единице, матрица поворота впоследствии преобразуется из необработанного пространства камеры непосредственно в выбранное цветовое пространство RGB, относящееся к выходу, и в то же время хроматически адаптирует исходный белый цвет исходного пространства камеры к эталонному белому пространству камеры. цветовое пространство, указанное на выходе.Было показано, что вариация элементов матрицы поворота цвета относительно CCT очень мала, поэтому требуется лишь небольшой выбор предварительно заданных матриц поворота, каждая из которых оптимизирована для заданного предварительно заданного источника света. Это позволяет применять необработанные множители каналов, подходящие для оценки WP освещения сцены, в сочетании с предварительно установленной матрицей поворота, связанной с наиболее подходящим WP. Основное преимущество переформулировки состоит в том, что интерполяция не требуется, и метод может быть эффективно реализован в архитектуре с фиксированной точкой.Кроме того, качество изображения может быть улучшено путем применения умножителей необработанных каналов до цветовой демозаики. Было показано, что DCRaw использует модель, аналогичную традиционным цифровым камерам, за исключением того, что для каждой камеры используется только одна матрица поворота цветов, в частности матрица R_D65, оптимизированная для освещения D65. Хотя общее преобразование цвета теряет некоторую точность, когда освещение сцены значительно отличается от D65, преимущество отделения множителей необработанного канала от характеристической информации, представленной матрицей поворота цвета, заключается в том, что WB может быть правильно достигнут для любого типа освещения сцены при условии необработанного применяются канальные множители, подходящие для освещения сцены.Было показано, что матрицы вращения, используемые DCRaw, могут быть получены из инверсий матриц цветовых характеристик ColorMatrix2, используемых конвертером Adobe DNG. Преобразователь Adobe DNG отображает необработанное пространство камеры и оценку WP освещения сцены на промежуточный этап в общем преобразовании цвета, а именно на PCS на основе цветового пространства CIE XYZ с WP D50. Метод 1 определяет подход, который также используется в коммерческих преобразователях необработанных данных и современных смартфонах. Цветовая матрица C_, оптимизированная для освещения сцены, получается посредством интерполяции между предварительно заданными матрицами «ColorMatrix1» с низким CCT и «ColorMatrix2» с высоким CCT.Из-за требований логики восстановления выделения эти цветовые матрицы отображаются в противоположном направлении по сравнению с обычными характеристическими матрицами. Кроме того, матрицы ColorMatrix1 и ColorMatrix2 изначально нормализованы в соответствии с WP PCS, а не их соответствующими характеристическими осветительными приборами. Поскольку цветовые матрицы Adobe находятся в свободном доступе, их соответствующим образом нормализованные инверсии могут служить полезными высококачественными характеристическими матрицами, когда оборудование для определения характеристик камеры недоступно. Метод 2, предлагаемый конвертером Adobe DNG, использует множители необработанных каналов аналогично традиционным цифровым камерам. Однако они применяются в сочетании с так называемой прямой матрицей, а не с матрицей вращения, поскольку преобразователь Adobe DNG напрямую не сопоставляется с цветовым пространством RGB, указанным на выходе, поэтому каждая строка прямой матрицы не суммируется до единицы. Хотя оптимизированная прямая матрица определяется путем интерполяции предварительно установленных матриц «ForwardMatrix1» и «ForwardMatrix2», изменение оптимизированной прямой матрицы относительно CCT очень мало, аналогично матрице вращения. Рассмотрим необработанные значения, выраженные как интегрирование по спектральной полосе пропускания камеры в соответствии с формулой. (5): R = k∫λ1λ2R1 (λ) E˜e, λdλ, G = k∫λ1λ2R2 (λ) E˜e, λdλ, B = k∫λ1λ2R3 (λ) E˜e, λdλ. Хотя E˜ e, λ можно рассматривать как среднюю спектральную освещенность на фотосъёмке, более точно это описывается как спектральная освещённость, свёрнутая с функцией рассеяния точки (PSF) системы камеры (x, y, λ) и измеренная в позиционных координатах ( x, y) на плоскости датчика: E˜e, λ (x, y) = [Ee, λ, ideal (x, y) * h (x, y, λ)] comb [xpx, ypy], где px и py — пиксель смолы в горизонтальном и вертикальном направлениях. Также может быть включена модель шума. 28 , 51 Величина, обозначенная Ee, λ, ideal (x, y), представляет собой идеальную спектральную освещенность в плоскости датчика, которая теоретически может быть получена в отсутствие системы PSF: Eλ, ideal (x, y) = π4Le, λ (xm, ym) 1Nw2T cos4 {φ (xm, ym)}, где Le, λ — соответствующая спектральная яркость сцены, m — увеличение системы, Nw — рабочее f-число объектива, T — коэффициент пропускания линзы, а φ — угол между оптической осью и указанными координатами сцены.Если известен профиль виньетирования объектива, четвертый член косинуса можно заменить коэффициентом относительной освещенности, который представляет собой функцию пространства изображения, описывающую реальный профиль виньетирования. 52 Константа k, которая появляется в уравнении. (5) устанавливает верхнюю границу величины необработанных значений. Можно показать 28 , что k задается как , где t — продолжительность воздействия, а gi — коэффициент преобразования между счетчиками электронов и исходными значениями для мозаики i, выраженный в единицах e- / DN. 53 , 54 Коэффициент преобразования обратно пропорционален усилению ISO GISO, которое является аналоговой настройкой усиления усилителя с программируемым усилением, расположенного перед АЦП: gi = UGISO, i, U = ne, i, FWCnDN, i, clip. Здесь U — единичный коэффициент усиления, который представляет собой настройку усиления, при которой gi = 1. Полнолуночная емкость обозначается символами ne, i, FWC и nDN, i, clip — это точка отсечения необработанного сигнала, которая представляет собой максимально доступный необработанный уровень. Это значение не обязательно равно максимальному необработанному уровню, обеспечиваемому АЦП с учетом его битовой глубины M, которая составляет 2M-1 DN, особенно если камера включает смещение смещения, которое вычитается перед записью необработанных данных. 28 , 53 Наименьшее аналоговое усиление определяется GISO = 1, что соответствует базовому усилению ISO. 28 , 51 Числовые значения соответствующих настроек ISO камеры S определяются с использованием выходных данных JPEG, а не необработанных данных. 55 , 56 Эти пользовательские значения также учитывают цифровое усиление, применяемое через градационную кривую JPEG. При сравнении необработанного вывода с камер, основанных на различных форматах датчиков, по возможности следует использовать эквивалентные, а не одинаковые настройки экспозиции. 57 Как указано в разд. 2.2, фактические необработанные значения, полученные на практике, представляют собой квантованные значения, смоделированные путем взятия целой части уравнения. (5), и полезно впоследствии нормализовать их до диапазона [0,1], разделив уравнение. (5) по необработанной точке отсечения. % PDF-1.5 Ур. (34)
Eq. (35)
Eq. (36)
5.
Традиционные цифровые камеры
Eq.(37)
Eq. (38)
Eq.(39)
Eq. (40)
Eq.(41)
Eq. (42)
Eq.(43)
5.1.
Умножитель и развязка матрицы
Рис. 8
Eq. (44)
Eq.(45)
5.2.
Пример: Olympus E-M1
Таблица 1
Диапазон CCT (K) Матрица вращения (фиксированная точка) Матрица вращения 2000 → 3000 [320−36−28−683081614−248490] [1.2500-0.1406-0.1094-0.26561.20310.06250.0547-0.96881.9141] 3100 → 3400 [332-52-24-58320-612-192436] [1.2969-0.2031-0.0938-0.22661.2500 −0.02340.0469−0.75001.7031] 3500 → 3700 [340−60−24−56324−1212−172416] [1.3281−0.2344−0.0938−0.21881.2656−0.04690.0469−0.67190.67190. 6250] 3800 → 4000 [346-68-22-52332-2410-160406] [1,3516-0,2656-0,0859-0,20311,2969-0.09380.0391−0.62501.5859] 4200 → 4400 [346−68−22−48332−2812−160404] [1.3516−0.2656−0.0859−0.18751.2969−0.10940.0107−06 4600 → 5000 [354−76−22−44336−3610−148394] [1,3828−0,2969−0,0859−0,17191,3125−0,14060,0391−0,57811,5391] 09 521000 → 56 [366−88−22−42340−4210−136382] [1.4297−0,3438−0,0859−0,16411,3281−0,16410,0391−0,53131,4922] 5800 → 6600 22 [374−96 −42348−508−124372] [1.4609-0,3750-0,0859-0,16411,3594-0,19530,0313-0,48441,4531] 6800 → 14000 [388-108-24-38360-668-112360] [1,51541-0,40219 .4063−0.25780.0313−0.43751.4063] Рис. 9
Таблица 2
Режим сцены CCT (K) Множители Матрица вращения (фиксированная точка) Хорошая погода 5300 474 256 414 [366–88 −22−42340−4210−136382] Прекрасная погода с тенью 7500 552 256 326 [388−108−24−38360−668−112360] Облачно 6000 510 256 380 [374−96−22−42348−508−124372] Вольфрам (накаливания) 3000 276 256 728 [320−36−28−683081614−248410090] Холодный белый люминесцентный 4000 470 256 580 [430−168−6−50300612−132376] Под водой 450 256 444 [366−88−22−42340−4210−136382] 009 Flash 5500 562 256 366 [366−88−22−42340−4210−136382] Ур. (46)
Ур.(47)
Рис. 10
6.
Конвертер RAW с открытым исходным кодом DCRaw
Eq. (48)
Eq. (49)
Eq.(50)
Eq. (51)
Таблица 3
-v Печатать подробные сообщения -w По возможности использовать WB камеры -A Среднее значение серого прямоугольника для WB -r Установить индивидуальный WB + M / -M Использовать / не использовать встроенную цветовую матрицу -H [0-9] Режим выделения (0 = клип, 1 = отсоединить, 2 = смешивание, 3+ = восстановление) -o [0-6] Цветовое пространство вывода (raw, sRGB, Adobe, Wide, ProPhoto, XYZ, ACES) -d Режим документа ( без цвета, без интерполяции) -D Режим документа без масштабирования (полностью необработанный) -W Не повышать яркость изображения автоматически -b Отрегулировать яркость по умолчанию = 1.0) -g Установить пользовательскую кривую гаммы (по умолчанию = 2,222 4,5) -q [0-3] Установить качество интерполяции -h Half -размер цветного изображения (вдвое быстрее, чем «-q 0») -f Интерполировать RGGB как четыре цвета -6 Записать 16-битное вместо 8-битного — 4 Линейный 16-битный, такой же, как «-6 -W -g 1 1» -T Записать TIFF вместо PPM 6.1.
Пример: Olympus E-M1
Ур. (52)
Ур.(53)
Eq.(54)
Eq. (55)
Eq. (56)
Ур.(57)
Eq. (58)
Ур. (59)
6.2.
DCRaw и MATLAB
7.
Adobe DNG
7.1.
Метод 1: Цветовые матрицы
Eq. (60)
Eq.(61)
7.2.
Нормализация цветовой матрицы
Eq. (63)
Eq. (64)
Eq. (65)
Eq. (66)
7.3.
Линейная интерполяция на основе обратной CCT
Eq. (67)
Eq. (68)
Eq. (69)
Рис. 11
Рис. 12
Рис. 13
7.4.
Метод 2: Прямые матрицы
Eq.(70)
Eq.(71)
Eq . (72)
Eq. (73)
Рис. 14
7.5.
Спецификация прямой матрицы
Ур. (74)
Eq. (75)
Eq. (76)
8.
Выводы
9.
Приложение: Модель необработанных данных
Eq.(77)
Eq. (78)
Eq. (80)
%
4 0 obj
>
эндобдж
7 0 объект
(Вступление)
эндобдж
8 0 объект
>
эндобдж
11 0 объект
(Определения и обозначения)
эндобдж
12 0 объект
>
эндобдж
15 0 объект
(Общие обозначения)
эндобдж
16 0 объект
>
эндобдж
19 0 объект
(Риманова геометрия)
эндобдж
20 0 объект
>
эндобдж
23 0 объект
(Дифференциалы, градиенты и гессианы)
эндобдж
24 0 объект
>
эндобдж
27 0 объект
(Группы Ли)
эндобдж
28 0 объект
>
эндобдж
31 0 объект
(Факторные пробелы)
эндобдж
32 0 объект
>
эндобдж
35 0 объект
(Римановы субмерсии)
эндобдж
36 0 объект
>
эндобдж
39 0 объект
(Группы Ли вращений SO \ (3 \) и SO \ (3 \) SO \ (3 \))
эндобдж
40 0 объект
>
эндобдж
43 0 объект
(Вывод существенной матрицы)
эндобдж
44 0 объект
>
эндобдж
47 0 объект
(Нормализованное существенное пространство)
эндобдж
48 0 объект
>
эндобдж
51 0 объект
(Нормализованное каноническое разложение)
эндобдж
52 0 объект
>
эндобдж
55 0 объект
(Неопределенность канонической формы)
эндобдж
56 0 объект
>
эндобдж
59 0 объект
(Геометрическая интерпретация с векторами изображений)
эндобдж
60 0 объект
>
эндобдж
63 0 объект
(Нормализованное существенное многообразие со знаком)
эндобдж
64 0 объект
>
эндобдж
67 0 объект
(Глубинная триангуляция)
эндобдж
68 0 объект
>
эндобдж
71 0 объект
(Нормализованное существенное пространство со знаком)
эндобдж
72 0 объект
>
эндобдж
75 0 объект
(Структура риманова фактор-многообразия)
эндобдж
76 0 объект
>
эндобдж
79 0 объект
(Геодезические и экспоненциальная карта)
эндобдж
80 0 объект
>
эндобдж
83 0 объект
(Расстояние и карта логарифма)
эндобдж
84 0 объект
>
эндобдж
87 0 объект
(Кривизна)
эндобдж
88 0 объект
>
эндобдж
91 0 объект
(\ (Беззнаковое \) нормальное существенное многообразие)
эндобдж
92 0 объект
>
эндобдж
95 0 объект
(Знаковое нормальное существенное многообразие как риманово накрытие)
эндобдж
96 0 объект
>
эндобдж
99 0 объект
(Сравнение с предыдущими составами)
эндобдж
100 0 объект
>
эндобдж
103 0 объект
(Оптимизация на существенном многообразии)
эндобдж
104 0 объект
>
эндобдж
107 0 объект
(Минимизация функции от E)
эндобдж
108 0 объект
>
эндобдж
111 0 объект
(Алгоритм Вайсфельда и усреднение позы)
эндобдж
112 0 объект
>
эндобдж
115 0 объект
(Заключение)
эндобдж
116 0 объект
>
эндобдж
119 0 объект
(Приложение.

 В реальной жизни, скорее всего, разница будет заметна ещё меньше. Стоит оно того или нет, решать только вам.
В реальной жизни, скорее всего, разница будет заметна ещё меньше. Стоит оно того или нет, решать только вам.