Что важнее размер матрицы фотоаппарата или количество мегапикселей?
Физический размер матрицы фотоаппарата, мегапиксели и качество снимков
По мере развития цифровой фото и видеотехники число мегапикселей, которыми производители приманивают покупателей, становится все больше. Но мало кто знает, что на самом деле для получения качественных фотографий гораздо важнее не разрешение, а физический размер самой матрицы.
Давайте разберем понятие мегапиксели. Пиксель — это одна маленькая точка из миллиона других, из которых состоит изображение.
Эти точки разные по размеру. Применительно к цифровой матрице, каждый пиксель — это миниатюрный датчик, на который при фотосъемке попадает свет, затем он преобразуется в цифровой сигнал и в таком виде передается в компьютер фотоаппарата. Таких датчиков на матрице огромное количество. Чем больше размер самой матрицы, тем больше размер каждого пикселя и их общее количество.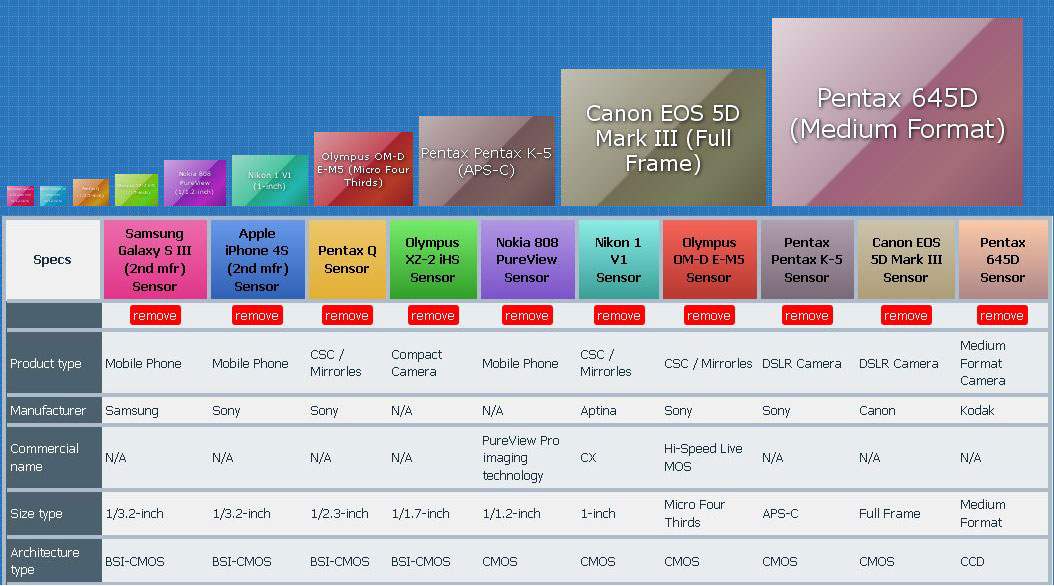 Поэтому зависимость между матрицей и качеством снимков – самая прямая.
Поэтому зависимость между матрицей и качеством снимков – самая прямая.
Вроде бы логично было бы писать эту площадь в виде длины и ширины, и желательно в миллиметрах. Но поскольку почти все параметры цифровой техники пришли к нам из-за границы, принято указывать размер матрицы в так называемых обратных дюймах, т.е. дробью, где в числителе единица, а в знаменателе – дюймовый размер матрицы. Например: 1/3.2 , 1/2.7 и т.д.
Большинству покупателей эти цифры мало о чем говорят.
Как правило, чем дешевле камера, тем меньше у нее физический размер матрицы и тем хуже качество сделанных ею фотографий.
Среди дорогих компактных камер иногда можно встретить модели с матрицей 2/3 , что обеспечивает неплохую детализацию снимков и достаточно высокую светочувствительность.
Матрицы 1/5 или 1/6 мы найдем в большинстве бюджетных зеркальных камер, это примерно половина кадра пленки 35 мм. Во многом именно за счет размера матрицы фотографии, сделанные зеркалкой, обычно выгодно отличаются от тех, которые сняты компактами.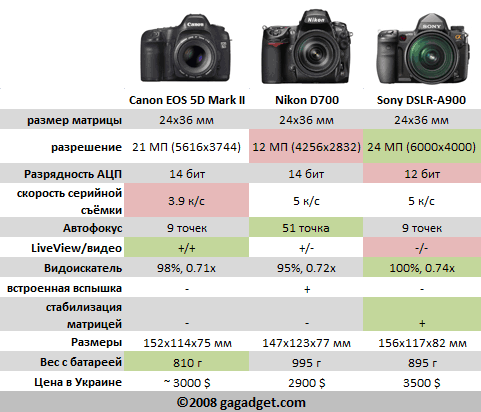
Есть еще полнокадровые матрицы (36х24 мм), которые по размеру соответствуют полному кадру 35 мм, и матрицы среднего формата (60х45 мм), которые больше этого стандартного кадра и применяются в дорогих зеркальных камерах.
Итак, на что же, собственно, влияет размер матрицы?
Первое – на размер и вес самой камеры. Фотоаппараты с небольшими матрицами компактны, их можно носить в кармане.
Камеры с большими матрицами, например, средний формат, приходится таскать в специальных кофрах, а то и вовсе использовать только в студии.
Второе – на увеличение цифрового шума — или, как еще по старинке говорят, зерна — на ваших снимках. «Шумные» фотографии выглядят так, будто изображение разбито на множество заметных цветных точек. Вид у них неопрятный, грязноватый.
Появление шума обусловлено тем, что на большую по площади матрицу попадает больше света, чем на маленькую. В результате передаваемый ею полезный сигнал будет лучшего качества, а отсюда – и лучшая проработка деталей, и более качественная цветопередача, и большая яркость картинки.
В результате передаваемый ею полезный сигнал будет лучшего качества, а отсюда – и лучшая проработка деталей, и более качественная цветопередача, и большая яркость картинки.
Кроме того, датчики большой матрицы расположены дальше друг от друга и изоляция между ними лучше, поэтому меньше пробивающих эту изоляцию токов, которые создают помехи, ухудшающие качество фотографий.
Отсюда, кстати, следует, что большое разрешение (те самые большие мегапиксели) при маленьком размере матрицы – скорее вредно, чем полезно.
Что будет, если на матрицу одного размера впихнуть 8 000 000 пикселей и 12 000 000? Во втором случае это приведет к уменьшению размера датчиков, ухудшению слоя изоляции между ними — и увеличению цифрового шума.
От разрешения матрицы в мегапикселях зависит то, какого размера снимки вы сможете напечатать без заметной потери качества. Разрешения 8 мегапикселей достаточно для печати фотографий формата А4 (альбомный лист). И при малом размере матрицы такое разрешение еще не приводит к заметному цифровому шуму.
Разрешения 8 мегапикселей достаточно для печати фотографий формата А4 (альбомный лист). И при малом размере матрицы такое разрешение еще не приводит к заметному цифровому шуму.
Выбирая себе фотоаппарат, обязательно обращайте внимание на физический размер матрицы, желательно чтобы он был максимально большим, насколько вы сможете себе позволить по финансам. От этого напрямую зависит качество сделанных фотографий, конечно если вы выберите зеркальную камеру, советую вам не покупать стандартный «китовый» объектив, который предлагают чаще всего в комплекте. Так как оптически он очень слабый и не надежный.
Но будьте готовы, что зеркальная камера с хорошим объективом будет стоить дороже компактного фотоаппарата да и будет не совсем миниатюрной.
Так что смотрите сами, что для вас важнее. Любые вопросы по фототехнике вы можете смело задать нашим фотографам:
+375-29-122-92-40 (Viber)
+375-29-122-92-40 (whatsApp)
E-mail: sales@sigma-foto. by
by
Skype: sigma-by
Пишите в чат фотографу!
Какой размер матрицы фотоаппарата лучше: таблица размеров
Рад вновь приветствовать вас, дорогой читатель. С вами на связи, Тимур Мустаев. Ранее на нашем блоге уже обозревались светочувствительные элементы фотоаппаратов, их свойства, кроп-фактор, количество мегапикселей и прочие параметры. Сегодня настал тот день, когда я вам расскажу более подробно, какой размер матрицы фотоаппарата лучше и почему.
В чём подвох?
Итак, если вы заинтересовались этой темой, значит, вы заинтересованы в улучшении качества своих фотографий. Вы, наверняка, уже слышали байку от рекламщиков, что на качество фотографии влияет только лишь количество мегапикселей. На самом деле, это не совсем так. Почему? Давайте разбираться.
Практически в каждом магазине фотооборудования есть, как минимум, один постер, кричащий о новой камере со встроенной матрицей супер высокого разрешения.
Естественно, стоить она будет много больше, чем «скромные» конкуренты, поэтому рекламировать их гораздо выгоднее.
Размер матрицы
Если говорить о габаритах датчика, то здесь любого читателя ожидает огромный диапазон вариантов. От миллиметровых сенсоров смартфонов до огромных светочувствительных элементов кинокамер. Я постараюсь затронуть лишь фотокамеры, насколько это будет возможно.
Итак, существует специальная классификация размеров матриц фотоаппаратов. Таблица, приведённая ниже, показывает более наглядно различия в их длине и ширине.
Как мы здесь видим, начинается с 1/3-½ дюйма. Как правило, такие сенсоры устанавливаются в наиболее дешёвых вариантах любительских мыльниц. Соотношение сторон таких матриц составляет 4:3. Вообще, этого достаточно для формирования семейного фотоальбома, но ведь мы не для этого начали так подробно изучать фотографию, верно?
Камеры с соотношением 2/3, 4/3 дюйма имеют такое же соотношение сторон, однако, пикселям на них более «комфортно», что положительно сказывается на качестве, потому применяются такие элементы на более дорогих фотоаппаратах.
Остальные варианты представляют собой сенсоры, с соотношением сторон 3:2, а также составляют половину от полного кадра. Последний пункт таблицы – Full Frame. Он полностью соответствует своему названию и представляет собой золотой стандарт – 35-миллиметровый светочувствительный элемент. 35-мм сенсор, кстати говоря, соответствует размеру плёнки старых камер, о чём уже говорилось ранее, в одной из прошлых статей.
Каков итог?
Настал тот момент, когда нужно формулировать тезисы. Итак, первый из них – чем шире и выше матрица, тем дальше пиксели находятся друг от друга. Как результат, пиксели «чувствуют себя более комфортно» в таких условиях: они меньше подвергаются перегреву и, сами по себе, имеют большие габариты, за счёт чего каждый из них может захватить большее количество света.
Исходя из этого, делаем вывод, что две камеры с одинаковым количеством мегапикселей и разной величиной сенсора получат различный конечный снимок. Камера с большим датчиком получит фотографию более качественную.
Мегапиксели
Как бы реклама не заверяла, что их количество сильно влияет на качество фотографии, это не совсем так. Вообще, число фотодиодов определяет не столько качество, сколько количество занимаемого в памяти объёма светового отпечатка, который передаётся на процессор. Конечно, высокое разрешение – это хорошо, только если они расположены на матрице соответствующего размера. Иначе, элементы будут перегревать друг друга, из-за чего на фотографиях может образоваться шум.
Благодаря тому, что огромное количество фотографов начинает разбираться в этом вопросе, производители начали создавать пиксели большей величины, чем раньше. А какой от этого толк?
Всё просто: площадь пикселя обширнее, следовательно, он способен захватить большее количество света и передать его на процессор для обработки.
Как мы знаем, многие камеры имеют определённый диапазон регулировки разрешения конечной фотографии. Так вот, подавляющая часть зеркалок имеют показатель от 12 до 24 Мп, а профессиональные – 10-36 Мп, причём площади сенсоров отличаются в 2 и более раз.
В чём смысл всего этого? Можно выбрать среднее разрешение меж двух крайних значений. Это обеспечит быструю обработку снимка и задействует лишь часть пикселей, из-за чего увеличится расстояние между работающими элементами. Такой лайфхак позволит избавиться от лишних шумов.
В чём же итог? Всё просто: под каждый случай будет хороша определённая матрица, однако, сравнение конечных результатов покажет превосходство полнокадрового датчика. Причиной тому универсальность последнего.
Если у вас есть зеркальная фотокамера и вы хотите научиться ею пользоваться, чтобы получать красивые фотографии, предлагаю вашему вниманию «Цифровая зеркалка для новичка 2.0» или «Моя первая ЗЕРКАЛКА». Данный видео курс, просто находка для новичка. Ознакомившись с его содержимым, вы получите отличные знания о зеркалки. Помните, саморазвитие — это большой шаг в будущее своего успеха.
Цифровая зеркалка для новичка 2.0 — у вас NIKON? Этот курс для вас.
Моя первая ЗЕРКАЛКА — у вас CANON? Этот курс для вас.
Надеюсь, у меня получилось рассказать о матрицах в фотоаппаратах, какая лучше и почему стоит выбирать больший сенсор. Если статья была интересна, а также полезна для вас – расскажите о ней друзьям, подпишитесь на обновления блога, впереди нас ждёт масса полезных фотостатей.
Всех вам благ, Тимур Мустаев.
Типы и размеры матриц камер видеонаблюдения
Светочувствительная матрица — важнейший элемент видеокамеры, который обеспечивает качество изображения на 90%. Представляет собой интегральную микросхему, состоящую из фотодиодов. Сенсор генерирует видеопоток, преобразуя проецируемое в него оптическое изображение в аналоговые электрические импульсы. В сетевых видеокамерах эти импульсы сразу преобразовываются в цифровой поток данных за счет наличия в системе АЦП, сразу обрабатывающего сигнал.
Сенсоры имеют ряд характеристик, важнейшие из которых — вид, разрешение и размер матрицы камеры видеонаблюдения. От этих параметров зависит быстродействие устройства, уровень его энергозатратности, а также конечное качество воспроизводимого камерой видео.
Типы матриц, которые используют в современных камерах видеонаблюдения
- CCD (ПЗС). Характеризуются лучшей светочувствительностью, обеспечивают хорошую цветопередачу и низкий уровень шума на изображении. Это достигается за счет последовательного считывания зарядов в каждой ячейке сенсора. Однако принцип действия таких матриц слишком медленный и не удовлетворяет современное видеонаблюдение с большими разрешениями и высокой кадровой частотой. Кроме того, такие сенсоры энергозатратны, дороже в производстве и сложнее в эксплуатации. В современных цифровых камерах важно какая матрица используется. Поэтому, чтобы не тормозить процесс передачи видеопотока, технологию CCD практически не применяют;
- Live-MOS. Разработка компании Panasonic. Применяется для трансляций «живого» изображения за счет технологии, которая позволяет упрощенно организовать передачу сигналов управления и преобразование света в электрические импульсы.
 Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;
Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех; - CMOS (КМОП). Главное достоинство — более низкое энергопотребление. Ячейки в сенсоре считываются в произвольном порядке, что позволяет избежать размытия изображения при съемке движущихся объектов. Камерой с типом матрицы CMOS гораздо проще управлять, поскольку большая часть электроники расположена на ячейке. Однако такая конструкция сенсора уменьшает светочувствительную площадь.
Для современного видеонаблюдения в соотношении быстродействия, энергопотребления и цены КМОП матрицы предпочтительнее. Поэтому крупнейшие производители камер сосредоточились на закупке или производстве собственных CMOS сенсоров. Например, компании Hikvision и Dahua разрабатывают собственные светочувствительные элементы, которые использует при производстве оборудования. В топовых видеокамерах Dahua DH-SD50430I-HC-S2 или HIKVISION DS-2CD2942F используются именно КМОП матрицы.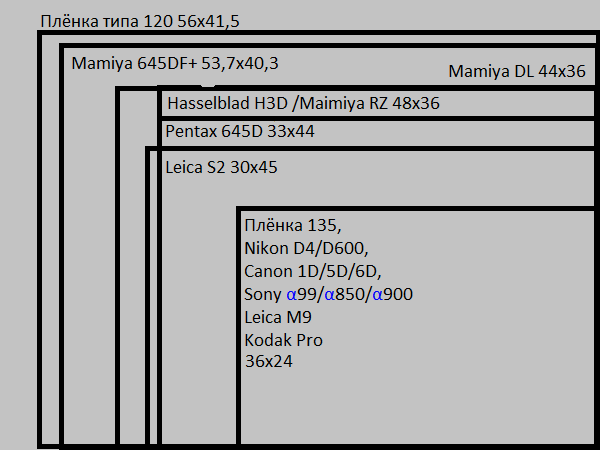
DH-SD50430I-HC-S2
Видеокамера HDCVI Скоростная купольная поворотная 4Мп разрешения
DS-2CD2942F
Панорамная купольная камера Fish Eye с высоким разрешением до 4Мп
ПЗС или КМОП матрица?
Размеры матриц видеокамер наблюдения
Физические размеры матриц выражаются условной длиной, приведенной к диагонали видикона.
Видикон — родоначальник современной фото- и видеотехники. Его диаметр равнялся 1 условному дюйму при рабочей диагонали 16 мм. «Видиконовый дюйм» принят стандартом для определения типоразмера матрицы. Таким образом, если указано, что сенсор имеет размер 1/2”, это значит, что его диагональ равна 8 мм.
Таким образом, если указано, что сенсор имеет размер 1/2”, это значит, что его диагональ равна 8 мм.
Современные видеокамеры чаще всего используют следующие типоразмеры: 1/2”; 1/3”; 1/4”; 1/6” и реже 1/10”.
На что влияет размер матрицы в камере?
От диагонали сенсора напрямую зависит качество изображения. Чем больше размер матрицы, тем крупнее у нее пиксели, следовательно, они улавливают большее количество света и расположены менее густо. Это позволяет уменьшить уровень помех, наводок и паразитных шумов. Кроме того, крупные сенсоры дают большие углы обзора для оптики с одинаковым фокусным расстоянием.
Какой размер матрицы лучше для видеокамеры
Это зависит от конкретных задач, стоящих перед видеонаблюдением. Важно помнить, что при выборе устройства характеристики нужно рассматривать комплексно. Например, хорошее разрешение при маленьком размере сенсора дадут плохое изображение. Кроме того, чем больше матрица, тем она дороже. Поэтому при выборе видеокамеры необходимо рассматривать вариант, в котором будут учитываться оптимальное соотношение трех показателей, удовлетворяющих потребности видеонаблюдения — это цена, разрешение и типоразмер.
Кроме того, чем больше матрица, тем она дороже. Поэтому при выборе видеокамеры необходимо рассматривать вариант, в котором будут учитываться оптимальное соотношение трех показателей, удовлетворяющих потребности видеонаблюдения — это цена, разрешение и типоразмер.
Типы и размеры матриц камер видеонаблюдения
Разберем характеристику первой попавшейся камеры.
| Матрица | 1/4″ Progressive Scan CMOS |
| Эффективных пикселей | 1Мп, 1280 х 720 |
Такую таблицу вы встретите на странице каждой камеры, меняются лишь значения, подставляемые к перечню характеристик. Как понять, что вам нужно и на какие данные стоит обратить внимание в первую очередь? Ведь матрица – это и есть та главная часть камеры, которая получает изображение, как фотопленка в старых фотоаппаратах.
Рассмотрим типы матриц. И начнем от обратного.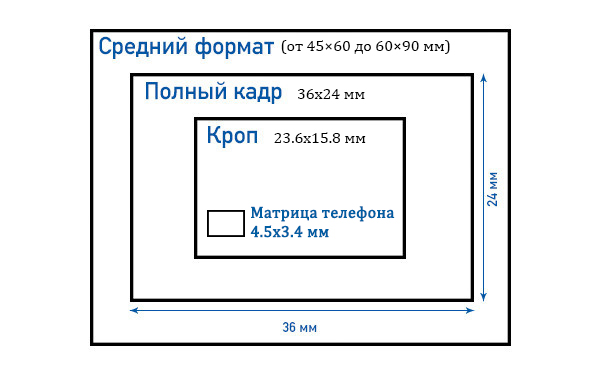 Матрицы, не использующиеся Hikvision – CCD-матрицы.
Матрицы, не использующиеся Hikvision – CCD-матрицы.
По сравнению с технологией CMOS, которую применяет в своих камерах Hikvision, CCD-матрицы позволяют создавать высококачественное изображение. В процессе съемки возникает гораздо меньше шумов, а бороться с все же возникшими намного легче, чем в матрицах CMOS.
Еще одним важным показателем является их высокая эффективность. Например, коэффициент заполнения у матриц CCD приближается к 100%, а соотношение зарегистрированных матрицей фотонов к их общему числу – 95%. Если сравнивать с нашими глазами, то при расчёте в тех же единицах соотношение составит только 1%.
К недостаткам CCD-матриц можно отнести сложность процесса. Для фиксации изображения в камере необходимо дополнительное наличие целого перечня устройств. Это приводит к более высокому энергопотреблению, делает их дороже в производстве и “капризнее” в эксплуатации.
Теперь о CMOS-матрицах.
Главное достоинство CMOS-матриц – более низкое энергопотребление и возможность произвольного считывания ячеек, а это CCD-матрице недоступно, там считывание происходит одновременно.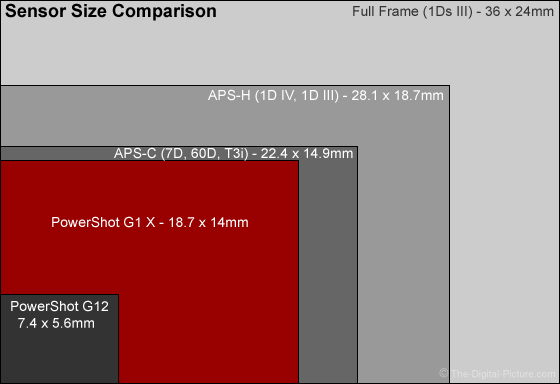 Благодаря произвольному считыванию в CMOS-матрицах нет размазывания изображения.
Благодаря произвольному считыванию в CMOS-матрицах нет размазывания изображения.
Еще одно достоинство – расположение значительной части электроники непосредственно на ячейке, благодаря этому появляются широкие возможности управления матрицей и изображением.
При всех имеющихся достоинствах данной технологии, недостатков хватает. Главный – незначительный размер светочувствительного элемента в соотношении к общей площади пикселя. Одно из основных достоинств – расположения электроники на ячейке. Но из него вытекает еще один недостаток – значительная часть площади пикселя занята электроникой, а значит, уменьшена площадь светочувствительного элемента.
В то же время нельзя не отметить, что CMOS был модифицирован несколько лет назад, и для видеонаблюдения CMOS-матрицы действительно подходят лучше (благодаря чёткому изображению, низкому энергопотреблению и возможности уменьшать битрейт видео.
типы, размер, разрешение, светочувствительность, чистка
Ни один фотоаппарат не может обойтись без матрицы.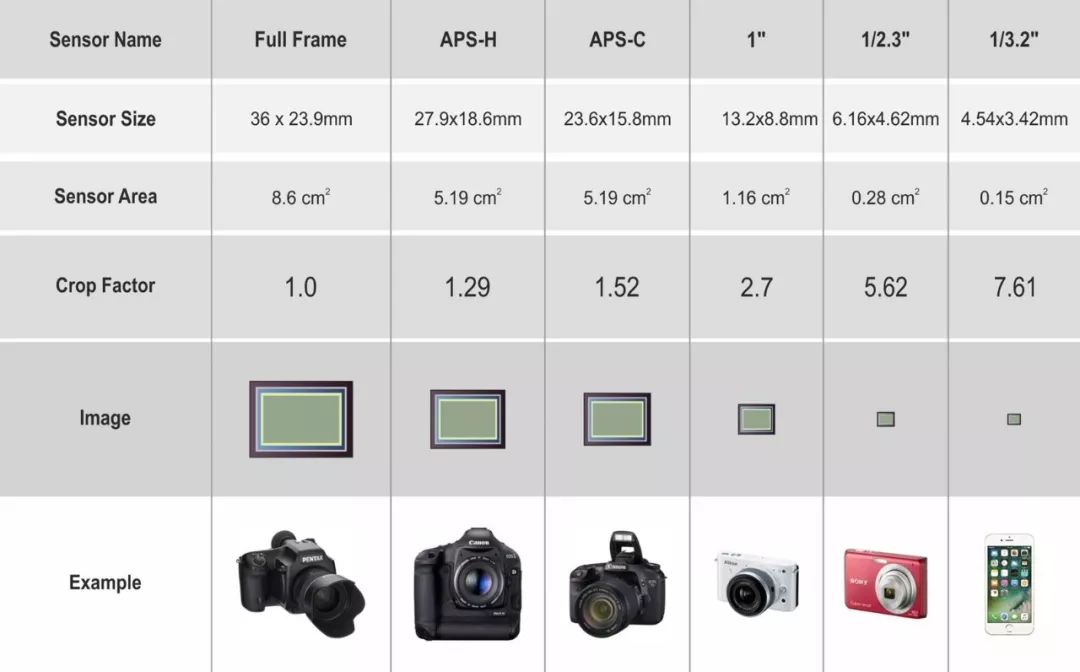 Современные модели оснащаются ей практически поголовно. Так произошло в момент, когда цифровые аналоги начали вытеснять устаревшие пленочные технологии. Матрица фотоаппарата является одним из основных компонентов, без которых невозможна эксплуатация всего прибора в целом, ведь его роль если и не является ключевой, то, по крайней мере, может считаться одной из ведущих. Именно матрица отвечает за качество будущего снимка, цветопередачу, четкость, полноту кадра. Как и другие важные элементы фототехники, матрица обладает рядом основных параметров, на которые обычно принято ориентироваться при выборе той или иной модели.
Современные модели оснащаются ей практически поголовно. Так произошло в момент, когда цифровые аналоги начали вытеснять устаревшие пленочные технологии. Матрица фотоаппарата является одним из основных компонентов, без которых невозможна эксплуатация всего прибора в целом, ведь его роль если и не является ключевой, то, по крайней мере, может считаться одной из ведущих. Именно матрица отвечает за качество будущего снимка, цветопередачу, четкость, полноту кадра. Как и другие важные элементы фототехники, матрица обладает рядом основных параметров, на которые обычно принято ориентироваться при выборе той или иной модели.
Типы матриц
Матрица цифрового фотоаппарата – это, в первую очередь, микросхема. Она преобразует световые лучи, которые, преломившись в системе линз и зеркал, попадают на нее. В результате такого преображения получается электрический сигнал, который выводится в цифровом виде, образуя снимок. За весь этот процесс отвечают специальные фотодатчики, расположенные на самой плате. Чем больше количество датчиков, чувствительных к свету, тем больше разрешение, и, как следствие, качество конечного снимка.
Чем больше количество датчиков, чувствительных к свету, тем больше разрешение, и, как следствие, качество конечного снимка.
Встречаются матрицы следующих типов.
- ПЗС – тип матрицы фотоаппарата, который дословно расшифровывается как прибор зарядовой связи. В английском варианте – Charge-Coupled Device. Весьма известная аббревиатура, которая, впрочем, не так часто встречается в наши дни. Многие используют приборы, в основе которых лежат светодиоды, имеющие высокую светочувствительность, созданные на основе ПЗС системы, но, несмотря на широкую распространенность, данный вид микросхем все больше вытесняется более современным.
- КМОП-матрица. Формат матрицы, введенный в эксплуатацию в 2008 году. Впрочем, история создания данного формата уходит корнями в далекий 93-й, когда впервые была опробована технология APS. КМОП-матрица – это комплиментарный металл-оксид-полупроводник. Данная технология позволяет производить выборку отдельного пикселя почти так же, как и в стандартной системе памяти, к тому же, каждый пиксель оснащается дополнительным усилителем.
 Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП.
Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП. - Существует еще один тип матрицы – Live-MOS-матрица. Ее выпустила фирма «Панасоник». Данная микросхема функционирует при помощи технологии, в основе которых лежит МОП. МОП-матрица позволяет делать качественные профессиональные снимки без высокого уровня шума, а также исключает перегрев.
Физический размер матрицы
Размер матрицы фотоаппарата – одна из ее важнейших характеристик. Как правило, его указывают в дюймах в виде дроби. Больший размер подразумевает меньшее количество шумов на конечном снимке. К тому же, чем больше физический размер, тем больше световых лучей способна зарегистрировать матрица. Объем и количество лучей напрямую влияют на качество передачи оттенков и полутонов.
Кроп-фактор — это соотношение размеров кадра пленочного фотоаппарата 35 мм к размерам матрицы цифрового фотоаппарата. Все дело в том, что процесс создания цифровой матрицы довольно дорогостоящий, и поэтому производители постарались максимально сократить ее размер.
Если сравнить фото, сделанное с одним объективом на фотоаппарате с полнокадровой матрицей и фотоаппарате с «кропнутой» матрицей, то в первом случае угол охвата будет больше, и само изображение шире. Получается, что кропнутая матрица обрезает готовую картинку, отсюда и пошло такое название – кроп от англ. crop (резать).
Чаще всего кроп-фактор используют для замера наиболее точного расстояния фокуса у объектива, устанавливая его на различные приборы. Здесь вступает в игру такое понятие, как эквивалентное фокусное расстояние (ЭФР), которое вычисляется путем умножения фокусного расстояния (ФР) на кроп-фактор. Так, объектив с полнокадровой матрицей (кроп=1) и объективом с ФР 50 мм зафиксирует такое же по размерам изображение, как и кропнутая матрица 1,6 с объективом с ФР 30 мм. В этом случае можно сказать, что ЭФР у этих объективов одинаковое. Ниже приведена таблица, в которой можно провести сравнение, как меняется ЭФР в зависимости от кроп-фактора.
В этом случае можно сказать, что ЭФР у этих объективов одинаковое. Ниже приведена таблица, в которой можно провести сравнение, как меняется ЭФР в зависимости от кроп-фактора.
Количество мегапикселей и разрешение матрицы
Матрица сама по себе является дискретной. Она состоит более чем из миллиона элементов, которые и преобразовывают световой поток, идущий от линз. В характеристике каждой модели фотоаппарата можно отыскать такой параметр матричной платы как количество светочувствительных элементов или разрешение матрицы, измеряемое в мегапикселях.
Один мегапиксель равен одному миллиону светочувствительных датчиков, улавливающих преломленные в линзах лучи. Разумеется, чем этот параметр будет больше, тем лучший снимок получится сделать.
Правда, здесь есть и обратная зависимость. Если физический размер матрицы меньше, то и количество мегапикселей должно быть пропорционально меньше, в противном случае не удастся избежать эффекта дифракции: фотографии будут замыленными, без четкости.
Чем больше размер пикселя, тем больше он способен зафиксировать лучей, падающих на него. Размер пикселей напрямую связан с размерами матрицы, и влияет, в основном, на широту кадра. Чем больше количество мегапикселей с правильным соотношением размеров матрицы, тем больше лучей света смогу уловить датчики. Количество зафиксированных лучей напрямую влияет на исходные параметры преобразуемого материала: резкость, цветность, объем, контрастность, фокус.
Таким образом, разрешение фотокамеры влияет на качество снимка. Зависимость разрешения от объема использующихся пикселей очевидна. В объективе при помощи сложной расстановки оптических элементов формируется необходимый световой поток, который потом матрица поделит на пиксели. Оптические приборы тоже обладают собственным разрешением. Более того, если разрешение объектива достаточно мало, а передача двух светящихся точек, разделяемых одной темной, происходит как единого целого, то разрешение будет не столь отчетливо выделяться. Происходит это именно из-за прямой зависимости и привязки к числу мегапикселей.
Происходит это именно из-за прямой зависимости и привязки к числу мегапикселей.
Важно: на качественный снимок влияет как параметр разрешения матрицы, так и разрешение оптики объектива. Измеряется оно количество линий на 1 мм. Своего максимального значения разрешение достигает, когда оба показателя — и матрица, и объектив — соответствуют друг другу.
Если говорить о разрешении современных цифровых микросхем, то оно складывается из размера пикселя (от 2 до 8 мкм). На сегодняшний день на рынке представлены модели с показателями до 30 мп.
Светочувствительность
В фотоаппаратах по отношению к матрице принято использовать термин эквивалентной чувствительности. Связано это с тем, что подлинную чувствительность можно измерять различными способами в зависимости от множества параметров матрицы. Зато, применив усиление сигнала и цифровую обработку, пользователь может обнаружить высокие пределы чувствительности.
Параметры светочувствительности демонстрируют возможность исходного материала преобразовываться из электромагнитных воздействий потока света в электрический двоичный сигнал. Проще говоря, показывать, сколько требуется света для получения объективного уровня электрического импульса на выходе.
Проще говоря, показывать, сколько требуется света для получения объективного уровня электрического импульса на выходе.
Параметр чувствительности (ISO) чаще всего используется фотографами для демонстрации возможности съемки в условиях плохого освещения. Увеличение чувствительности в параметрах прибора позволяет улучшить качество конечного снимка при необходимом значении диафрагмы и выдержки. ISO может достигать значения от нескольких десятков до тысяч и десятков тысяч единиц. Негативной стороной высоких значений светочувствительности является появление «шумов», которые проявляются в виде эффекта зернистости кадра.
Как проводить чистку матрицы в домашних условиях
Битые пиксели не всегда могут быть таковыми на самом деле. В действительности, когда происходит смена объектива, на матрицу могут попасть частицы мусора, вызывающие эффект «битого пикселя». Чистка матрицы фотоаппарата нужна для профилактики этого эффекта, а также для более комфортной работы с прибором.
Со временем, в особенности, если устройство эксплуатируется подолгу в различных погодных условиях, матрица может покрыться слоем пыли. При нарушении герметичности в области крепления объектива на поверхность может попасть небольшое количество влаги, что тоже может негативно сказаться на качестве кадра. Чистку можно доверить профессионалам из сервисного центра, а можно провести и самостоятельно, в домашних условиях.
Важно не забывать, что помещение, в котором будет происходить процедура, должно быть как можно менее пыльным, без сильных сквозняков. Прежде чем приступать к самой процедуре, необходимо убедиться, что аккумуляторная батарея заряжена.
Первый и самый простой способ очистки стеклянной поверхности кремниевой пластины микросхемы – сдувание пыли. Для этого следует использовать самую обычную грушу для чистки объективов, она продается в любом крупном магазине бытовой техники. К сожалению, использование груши помогает только при снятии легкого налета небольших песчинок пыли. Для более крупных частиц, которые могли прилипнуть к поверхности, может потребоваться что-то более основательное.
Для более крупных частиц, которые могли прилипнуть к поверхности, может потребоваться что-то более основательное.
Если груша не помогла справиться с пятнами на матрице, можно попробовать использовать специальный набор для очистки стеклянной поверхности. Стоит он несколько дороже, но эффективность очистки значительно выше.
- Первый пункт в очистке – использование специального пылесоса. Его сборка не занимает много времени и детально описана в инструкции к набору. На конце устройства находится мягкий наконечник, так что повреждение прибора во время работы исключено. Лучше всего будет прочистить при помощи пылесоса не только стеклянную поверхность, но и все скрытые полости, доступные для чистки.
- После уборки при помощи пылесоса можно начинать влажную уборку. Она осуществляется при помощи специальных щеточек, одна из которых влажная, другая сухая. Этот вид уборки нужен для пылинок, которые, будучи мокрыми, попали на поверхность стекла, и, высохнув, прикрепились к нему, создав эффект «битого пикселя».
 Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).
Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой). - Третий этап – финальный, проводим сухой щеточкой по матрице и убеждаемся, что она чистая.
После очистки можно попробовать сделать тестовый снимок, чтобы убедиться, что процедура прошла успешно. Для этого необходимо закрыть диафрагму до максимального значения и сделать снимок чистого белого листа, приведя объектив в состояние полной расфокусировки. Затем сравнить качество снимков до и после.
Почистить матрицу зеркального фотоаппарата довольно просто, для этого не требуется каких-то глубоких знаний или большого опыта, достаточно желания, немного терпения и знания базовых принципов очистки высокоточной оптической техники.
Заключение
Матрица фотоаппарата является важнейшей деталью любой современной зеркалки. Без нее невозможно сделать снимок, а от ее параметров зависит дальнейшее использование устройства. Если параметры матрицы выбраны неправильно, фотоаппарат не будет оптимально справляться со своими задачами. Матрица не требует какого-то дополнительного ухода, кроме периодической чистки стеклянной поверхности.
Следует отметить, что светочувствительные датчики очень хрупкие и плохо переживают падение прибора даже с небольшой высоты, поэтому эксплуатировать фотоаппарат рекомендуется с максимальной осторожностью и аккуратностью.
Размер пикселя и разрешение матрицы цифровой камеры
Принимая решение, какую купить цифровую камеру для телескопа или цифровую камеру для микроскопа, Вы можете заметить, что в описании их технических характеристик указан такой параметр как размер пикселя. Давайте разберемся, за что отвечает данная величина, и какой цифровой камере в таком случае следует отдать предпочтение.
Давайте разберемся, за что отвечает данная величина, и какой цифровой камере в таком случае следует отдать предпочтение.
Прежде всего, считаем, что нужно дать определение термину «пиксель». Понятие пиксель происходит от английского словосочетания picture element, что в переводе означает «элемент изображения». Так, говоря о пикселях, мы имеем в виду точки, образующие изображение на экране монитора. И отметим, что в формировании снимка, сделанного цифровой камерой, может участвовать даже несколько миллионов подобных точек.
А теперь давайте выясним, на что влияет размер этой точки, т.е. пикселя. От физического размера пикселя зависит количество собираемого им света. Поэтому чем крупнее пиксель, тем, соответственно, больше его площадь, а, значит, и количество собранного света. Таким образом, получаем, что чем больше физический размер пикселя, тем выше светочувствительность матрицы и лучше соотношение сигнал/шум.
Также заметим, что цифровые компактные фотоаппараты, которые часто еще называют мыльницами или цифромыльницами, при одинаковом количестве пикселей имеют гораздо меньшие размеры матрицы, чем обычные цифровые камеры. По этой причине мы получаем меньшие физические размеры пикселей на матрицах цифромыльниц. Таким образом, мы видим, что размеры пикселей оказывают существенное влияние на качество получаемого изображения, количество шумов и динамический диапазон. Отметим, что в пленочной фотографии шумы также еще могут называть «вуалью».
По этой причине мы получаем меньшие физические размеры пикселей на матрицах цифромыльниц. Таким образом, мы видим, что размеры пикселей оказывают существенное влияние на качество получаемого изображения, количество шумов и динамический диапазон. Отметим, что в пленочной фотографии шумы также еще могут называть «вуалью».
Так от физического размера пикселей зависит:
-
Количество информации, попадающей на него -
Динамический диапазон матрицы -
Шумы
Нельзя ожидать, что решив купить цифровую камеру для телескопа или микроскопа с небольшим физическим размером матрицы и большим количеством пикселей, Вы получите качественный снимок.
Следует понимать, что чем меньшие размеры пикселя матрицы цифровой камеры, тем раньше проявляется дифракция, и получаемое изображение начинает мылить (собственно, отсюда и происходит название «мыльница»).
Сегодня производители цифровых камер предлагают цифровые камеры с разрешением, которое может достигать даже десятков миллионов пикселей. Чем большее количество пикселей указано в технических параметрах цифровой камеры для микроскопов и телескопов, тем большим будет разрешение матрицы цифровой камеры, а, следовательно, тем выше будет детализация полученного снимка.
Чем большее количество пикселей указано в технических параметрах цифровой камеры для микроскопов и телескопов, тем большим будет разрешение матрицы цифровой камеры, а, следовательно, тем выше будет детализация полученного снимка.
Вывод:
Итак, при выборе цифровой камеры для микроскопа или телескопа рекомендуем Вам учитывать, что:
-
Чем больше физический размер пикселя, => тем большее количество информации на него попадает, и тем больше будет динамический диапазон матрицы, и меньше будут сказываться шумы. -
Чем выше разрешение матрицы, => тем более четкое и детализированное изображение Вы получите и, тем большего размера фотографию будет возможно напечатать без ощутимой потери качества.
Автор статьи: Галина Цехмистро
Матрица цифровой камеры. Типы и размер матриц
Выбирая цифровую камеру для микроскопа или телескопа, часто обращают внимание лишь на разрешение матрицы, т. е. количество мегапикселей. Однако это не единственный важный параметр цифровой камеры, определяющий качество полученных фотоснимков и видеороликов. По каким же признакам следует выбирать цифровую камеру, и чем они могут отличаться одна от другой?
е. количество мегапикселей. Однако это не единственный важный параметр цифровой камеры, определяющий качество полученных фотоснимков и видеороликов. По каким же признакам следует выбирать цифровую камеру, и чем они могут отличаться одна от другой?
Главным элементом цифровой камеры является ее матрица, которая, собственно, и фиксирует изображение в цифровой камере. Отметим, что также в техническом описании цифровых камер часто употребляется и термин сенсор, обозначающий то же, что и матрица. Матрица состоит из массива светочувствительных ячеек, и именно от нее зависит качество изображения, полученного с помощью цифровой камеры.
Существует два основных типа матриц: CCD (ПЗС матрицы) и CMOS (КМОП матрицы), отличающиеся по применяемой технологии. И если на рынке фотоаппаратов наиболее распространены цифровые камеры с ПЗС матрицей, то большинство моделей цифровых камер для телескопов и микроскопов имеют именно КМОП матрицу.
Чем же отличается ПЗС матрица от КМОП матрицы? Основным их отличием является то, что в ПЗС матрицах информация из ячеек считывается последовательно, в то время как в КМОП матрицах информация считывается индивидуально из каждой отдельной ячейки. По этой причине в ПЗС матрицах Вы не можете сделать следующий снимок до тех пор, пока не будет целиком сформирован предыдущий. Что же касается КМОП матриц, то благодаря применяемой технологии их можно использовать не только для фотосъемки, но и для экспонометрии и работы автофокуса. Помимо этого, КМОП матрицы гораздо дешевле в производстве, и поэтому доступнее для многих пользователей. Еще одно немаловажное преимущество КМОП матриц над ПЗС матрицами – потребление меньшего количества энергии.
Первым делом при выборе цифровой камеры мы рекомендуем Вам обратить внимание на размер матрицы. Физическим размером матрицы называется ее геометрический размер, т.е. длина и ширина матрицы, выраженные в мм. Физический размер матрицы определяет ее качество. Узнать значение этого параметра можно из ее технического описания, хотя, как правило, размеры фотосенсоров производители указывают не в мм, а введя специальное обозначение типа матрицы в виде дробных частей дюйма, например: 1/4″, 1/3″, 1/2.5″, 1/2″ и пр. Сравнивая различные цифровые камеры, Вы должны понимать, что размер матрицы больше у той цифровой камеры, у которой знаменатель в указанной дроби будет меньше, т.е. сенсор 1/2″ будет больше сенсора 1/3″.
Физический размер матрицы определяет ее качество. Узнать значение этого параметра можно из ее технического описания, хотя, как правило, размеры фотосенсоров производители указывают не в мм, а введя специальное обозначение типа матрицы в виде дробных частей дюйма, например: 1/4″, 1/3″, 1/2.5″, 1/2″ и пр. Сравнивая различные цифровые камеры, Вы должны понимать, что размер матрицы больше у той цифровой камеры, у которой знаменатель в указанной дроби будет меньше, т.е. сенсор 1/2″ будет больше сенсора 1/3″.
Какая же связь между физическим размером матрицы, указанным в мм и типом матрицы, выраженном в 1/дюйм? Отметим, что введенное обозначение типа матрицы выражает не размер ее диагонали, а внешний размер колбы передающей трубки. Обратите внимание на то, что не существует конкретной математической формулы, четко выражающей взаимосвязь между устоявшимся обозначением типа матрицы, выраженного в 1/дюйм, и самим физическим размером диагонали матрицы в мм. Тем не менее, в грубом приближении принято считать, что диагональ сенсора равна двум третям его типоразмера.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вполне целесообразно задать вопрос, а на что же влияет размер матрицы? Прежде всего, сколь иронично это бы не звучало, размер матрицы цифровой камеры влияет на ее стоимость и вес.
Помимо этого, как мы уже отмечали ранее, размер сенсора влияет на качество полученных фотоснимков и видеороликов. Во-первых, от размера сенсора зависит количество цифрового шума, который передается на светочувствительные элементы матрицы вместе с основным сигналом.
Из-за цифрового шума полученные снимки получают неестественный вид, в связи с чем возникает такое ощущение, что сверху на снимок наложена маска из точек различного цвета и яркости.
Причинами возникновения шумов могут быть дефекты в структуре сенсора, токи утечки (заряд может пробивать изоляцию и переходить с одного пикселя на другой), нагрева матрицы (так называемый тепловой шум, когда при повышении температуры на 6-8 градусов шум увеличивается в 2 раза) и пр.
Конечно же, нужно понимать, что абсолютно бессмысленно рассматривать показатель шума отдельно – важно соотношение сигнал / шум.
Итак, на количество шумов главным образом влияет физический размер матрицы, а также размер пикселя. Чем больше физический размер сенсора цифровой камеры, тем больше его площадь и, соответственно тем больше света попадает на него. А, следовательно, полезный сигнал матрицы будет сильнее и, значит, мы получим лучшее соотношение сигнал / шум, что обеспечит более яркое и качественное изображение с более правильной и естественной цветопередачей.
Помимо этого, отметим, что слой изоляции, разделяющий пиксели друг от друга, будет толще для пикселей большого размера. Разумеется, что чем толще слой изоляции, тем меньше зарядов смогут пробить ее. Следовательно, токов утечки будет тоже меньше, что соответственно приведет и к уменьшению шумов.
В качестве примера предлагаем Вам представить матрицу определенного размера. Предположим, что на одной такой матрице 3000 пикселей (3 Мпикс), а на второй такой же матрице расположено 5000 (5 Мпикс). А теперь представьте толщину изоляции пикселей для первого и для второго случая!
Еще раз отметим, что чем меньше матрица, тем меньшее количество света на нее попадает. В таком случае Вы получаете слабый полезный сигнал, который приходится усиливать. А с усилением полезного сигнала естественно усиливаются и становятся более заметными шумы.
В заключение еще раз повторим, что чем больше физический размер матрицы, тем большее количество света на нее попадает, а значит, тем более качественно изображение Вы получите.
Автор статьи: Галина Цехмистро
Размер матрицы — обзор
Мы используем одну (или в нижнем индексе) жирную заглавную букву для обозначения матрицы (например, A , B , C 1 , C 2 ) в отличие от строчных полужирных букв, используемых для обозначения векторов. Заглавные буквы I и O обычно зарезервированы для специальных типов матриц, обсуждаемых позже.
Размер матрицы всегда указывается первым числом строк.Например, матрица 3 × 4 всегда имеет три строки и четыре столбца, а не четыре строки и три столбца.
Матрица m × n может рассматриваться как набор векторов-строк m , каждый из которых имеет координаты n , или как набор векторов-столбцов n , каждый имеющий координаты м . Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).
Мы часто пишем a ij для представления записи в строке i и j -м столбце матрицы A . Например, в предыдущей матрице , , , , , 23, — это запись -5 во второй строке и третьем столбце. Типичная матрица 3 × 4 C имеет элементы, обозначенные как
C = [c11c12c13c14c21c22c23c24c31c32c33c34].
ℳ mn представляет собой набор всех матриц с записями действительных чисел, имеющими m строк и n столбцов.Например, ℳ 34 — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ 34 имеет форму предшествующей матрицы C .
главная диагональ элементов матрицы A — это a 11 , a 22 , a 33 ,…, те, которые лежат на диагональной линии рисуются вправо, начиная с верхнего левого угла матрицы.
Матрицы и матричная алгебра — Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: дополнительные примеры
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
Матрицы
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список, подобный этому: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы придерживаться соглашения.
Некоторые из наиболее распространенных терминов, с которыми вы встретитесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т.е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерностей должно быть точно так же, как . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одно и то же место (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: на листе (например, в Excel) буквы столбцов (ABCD) и номера строк (123) используются для определения местоположения ячейки, например A1 или D2. Для матриц типично использование обозначений типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Вычитание матриц работает точно так же.
Наверх
Дополнение Matrix — это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в правом верхнем углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Добавление матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Например:
К началу
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Если вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице.Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете умножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива».Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
Наверх
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Есть и другие типы сингулярных матриц, некоторые из них не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет обратного.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица — это квадратная матрица, но не все квадратные матрицы сингулярны.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Если вы не знакомы с поиском инверсий, вы можете посмотреть это короткое видео:
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы.Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началу
Единичная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах. Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным.Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x. По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n . На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Матрица аддитивной идентичности
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули. Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.
Поиск обратной матрицы состоит из нескольких шагов. Посмотрите это короткое видео о том, как найти обратную матрицу, или выполните следующие действия:
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ с помощью умножения матриц. Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
Наверх
Собственное значение (λ) — это специальный скаляр, используемый при умножении матриц и имеет особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем.Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его по вектору x .
Пример собственного значения
В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что, если бы вместо новой матрицы nx 1 можно было получить ответ с тем же вектором, который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в разложении на собственные числа . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ 2 — 9
= λ 2 — 4λ — 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
Наверх
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Можно поместить в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас не , а , чтобы использовать вертикальную полосу в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце со знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом шаге стоит отрицательный знак, просто сделайте константу отрицательным числом.
Наверх
Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A — это | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два понятия не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые входят в матрицу 4 × 4.В виде формулы:
Наверх
Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая имеет все 1 по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы, — diag (a, b, c) , где abc представляет числа в первой диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. Нижнетреугольная матрица имеет числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица — это матрица с нижней диагональю и матрица с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n . Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
Наверх
Транспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Формально A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы — A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их транспонированных матриц в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
Наверх
Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. транспонирование матрицы — это когда первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T — матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричным аналогом является -4 в строке 2, столбце 3. Это условие также можно записать в терминах его матрицы транспонирования: A T = — А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T — это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что из i, i = −a i, i следует i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на ведущей диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = — a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).
Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Дисперсия — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что в основном эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте дисперсии для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A). На следующей диаграмме показано, где каждая ковариация и дисперсия появляются для каждого варианта.
Наверх
См. Также:
Что такое матрица неточностей?
Следующий : Форма эшелона строк / Форма сокращенного эшелона строк
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
c — Умножение матриц: небольшая разница в размере матрицы, большая разница во времени
Вы определенно получаете то, что я называю кэшем , резонансным . Это похоже на псевдоним , но не совсем то же самое. Позволь мне объяснить.
Кеши — это аппаратные структуры данных, которые извлекают одну часть адреса и используют ее в качестве индекса в таблице, в отличие от массива в программном обеспечении. (Фактически, мы аппаратно называем их массивами.) Массив кеша содержит строки кэша данных и теги — иногда одна такая запись на каждый индекс в массиве (прямое отображение), иногда несколько таких (N-сторонняя ассоциативность набора).Вторая часть адреса извлекается и сравнивается с тегом, хранящимся в массиве. Вместе индекс и тег однозначно идентифицируют адрес памяти строки кэша. Наконец, остальные биты адреса определяют, какие байты в строке кэша адресованы, а также размер доступа.
Обычно индекс и тег представляют собой простые битовые поля. Таким образом, адрес памяти выглядит как
... Тег ... | ... Указатель ... | Offset_within_Cache_Line
(Иногда индекс и тег являются хешами, например.грамм. несколько XOR других битов в биты среднего диапазона, которые являются индексом. Гораздо реже, иногда индекс, а реже тег — это такие вещи, как получение адреса строки кэша по модулю простого числа. Эти более сложные вычисления индекса — это попытки решить проблему резонанса, которую я объясняю здесь. Все страдают той или иной формой резонанса, но, как вы обнаружили, простейшие схемы извлечения битового поля страдают резонансом с общими шаблонами доступа.)
Итак, типичные значения … есть много разных моделей «Opteron Dual Core», и я не вижу здесь ничего, что указывало бы на то, какая из них у вас есть.Выбирая одно наугад, последнее руководство, которое я вижу на веб-сайте AMD, Bios and Kernel Developer’s Guide (BKDG) для AMD Family 15h Models 00h-0Fh, 12 марта 2012 г.
(Семейство 15h = семейство Bulldozer, новейшие высокопроизводительные процессоры — в BKDG упоминается двухъядерный процессор, хотя я не знаю номер продукта, который вы точно описываете. Но, в любом случае, одна и та же идея резонанса применима ко всем процессорам , просто такие параметры, как размер кэша и ассоциативность, могут немного отличаться.)
Со стр.33:
Процессор AMD семейства 15h содержит 16-килобайтный 4-сторонний прогнозируемый L1
кэш данных с двумя 128-битными портами. Это кэш со сквозной записью, который
поддерживает до двух 128-байтовых нагрузок за цикл. Он разделен на 16
банки шириной 16 байт каждый. […] Только одна загрузка может быть выполнена из
данный банк кеш-памяти L1 за один цикл.
Итого:
64-байтовая строка кэша => 6 битов смещения в строке кэша
16 КБ / 4-полосный => резонанс 4 КБ.8 = 256 строк кэша в кеше.
(Исправление: изначально я неправильно рассчитал это как 128. что я исправил все зависимости.)4-сторонняя ассоциативная => 256/4 = 64 индекса в массиве кеша. Я (Intel) называю эти «наборы».
, то есть вы можете рассматривать кеш как массив из 32 записей или наборов, каждая запись содержит 4 строки кеша и их теги. (Это сложнее, но это нормально).
(Кстати, термины «набор» и «путь» имеют разные определения.)
есть 6 бит индекса, биты 6-11 в простейшей схеме.
Это означает, что любые строки кэша, которые имеют точно такие же значения в битах индекса, биты 6-11, будут отображаться в один и тот же набор кэша.
Теперь посмотрим на свою программу.
C [размер * i + j] + = A [размер * i + k] * B [размер * k + j];
Цикл k — это самый внутренний цикл. Базовый тип — двойной, 8 байт. Если размерность = 2048, то есть 2К, то последовательные элементы B [размер * k + j] , к которым обращается цикл, будут разделены на 2048 * 8 = 16 Кбайт.Все они будут отображаться в один и тот же набор кеша L1 — все они будут иметь один и тот же индекс в кеше. Это означает, что вместо 256 строк кэша, доступных для использования, будет только 4 — «четырехсторонняя ассоциативность» кеша.
Т.е. вы, вероятно, будете получать пропуски кеша каждые 4 итерации этого цикла. Нехорошо.
(На самом деле все немного сложнее. Но вышесказанное является хорошим первым пониманием. Адреса записей B, упомянутых выше, являются виртуальными адресами.Так что физические адреса могут немного отличаться. Более того, Bulldozer имеет способ кеширования с прогнозированием, вероятно, использующий биты виртуальных адресов, чтобы не ждать преобразования виртуального адреса в физический. Но, в любом случае: ваш код имеет «резонанс» 16К. Кэш данных L1 имеет резонанс 16К. Не хорошо.)]
Если вы немного измените размер, например до 2048 + 1, то адреса массива B будут распределены по всем наборам кеша. И вы получите значительно меньше промахов в кеш-памяти.
Это довольно распространенная оптимизация для заполнения ваших массивов, например изменить 2048 на 2049, чтобы избежать этого резонанса. Но «блокировка кеша — еще более важная оптимизация. Http://suif.stanford.edu/papers/lam-asplos91.pdf
Помимо резонанса строки кэша, здесь происходят и другие вещи. Например, кэш L1 имеет 16 банков, каждый по 16 байт. При размерности = 2048 последовательные обращения к B во внутреннем цикле всегда будут происходить в одном и том же банке. Таким образом, они не могут работать параллельно — и если доступ A попадет в тот же банк, вы проиграете.
Я не думаю, глядя на это, что это такое же большое, как резонанс кеша.
И, да, возможно, есть алиасинг. Например. Буферы STLF (Store To Load Forwarding) могут сравнивать только с использованием небольшого битового поля и получать ложные совпадения.
(На самом деле, если подумать, резонанс в кэше похож на наложение, связанный с использованием битовых полей. Резонанс возникает из-за того, что несколько строк кэша отображают один и тот же набор, а не распространяются по всему миру. Алисинг вызывается сопоставлением на основе неполного адресные биты.)
В целом моя рекомендация по тюнингу:
Попробуйте заблокировать кеш без дальнейшего анализа. Я говорю это, потому что блокировать кеш легко, и очень вероятно, что это все, что вам нужно сделать.
После этого используйте VTune или OProf. Или Cachegrind. Или …
А еще лучше использовать хорошо настроенную библиотечную процедуру для матричного умножения.
вложений: матрица смысла. Адам Шваб | компании Petuum, Inc.
Адам Шваб
Как мы можем смоделировать , означающую слова? Когда мы думаем о глаголе «бегать», он вызывает чувство напряжения или, возможно, изображение марафона. Можем ли мы представить слово как узел на графике или смоделировать его как изображение? На протяжении веков вопрос о том, как моделировать значение, оставался философам, а в последние сто лет — психологам и лингвистам. За последние двадцать лет этот вопрос стал критически важным для мира искусственного интеллекта и информатики.
В этом контексте мы можем эмпирически исследовать значения слов. Концепция матрицы внедрения оказалась полезной как для понимания лингвистики, так и для решения реальных проблем в области обработки естественного языка.
Возьмите три похожие фразы:
- … когда рабочий ушел…
- … когда ушел рыбак…
- … когда собака ушла…
А теперь представьте, что мы не знаем, что Значит « рабочий », « рыбак», и « собака» .На самом деле мы не знаем ни одного слова, но легко можем сказать, что фразы идентичны, за исключением одного слова. Поскольку контексты идентичны, мы можем экстраполировать, что существует некоторое сходство между « рабочий», «рыбак», и « собака» . Применяя эту идею ко всему корпусу, мы могли определить отношения между словами. Затем мы подходим к вопросу о том, как лучше всего представить эти отношения в общем виде.
Концепция матрицы вложения — это попытка решить эту проблему представления отношений.Для начала мы выбираем размерность значения — это может быть несколько произвольно. Скажем, мы решили, что все значения могут отображаться в некотором абстрактном трехмерном пространстве. Концептуально это будет означать, что все слова будут существовать как особые точки в трехмерном пространстве, и любое слово может быть однозначно определено своим положением в этом пространстве, описываемым тремя числами (x, y, z). Но на самом деле значение слишком сложно, чтобы уместиться в трех измерениях. Обычно мы используем что-то вроде 300 измерений, и все слова сопоставляются с какой-то точкой в этом 300D гиперпространстве и определяются 300 числами.Мы называем 300 чисел, которые идентифицируют данное слово, с вложением для этого слова.
Теперь отношения между словами могут быть представлены путем сравнения вложений слов. Например, «рабочий» сопоставляется с W , который является вектором длиной 300, а «рыбак» сопоставляется с F , который представляет собой другой вектор длиной 300. Связь между двумя словами можно описать как их различие: W – F . Обратите внимание, что это не коммутативно (x – y! = Y – x), но отношения слов друг к другу также не коммутативны.Отношения между « человека» и « человека» не такие, как наоборот. Направление отношений на самом деле содержит в себе смысл — что можно сделать с « человека», , чтобы превратить его в « человека»?
Матрица вложения — это список всех слов и соответствующих им вложений.
Следует помнить о нескольких вещах:
- Думать в высших измерениях сложно. Не увлекайтесь размерами.Та же концепция работает (хотя и не так хорошо) в трех измерениях.
- В реальном мире каждое измерение имеет очевидный физический смысл — как оси XYZ нашего трехмерного мира. В пространстве вложения мы обычно не определяем оси — большую часть времени мы даже не знаем, что представляет собой конкретная ось в нашем гиперпространстве вложения. Вместо этого мы используем другие инструменты для расшифровки полезности из матрицы.
- Обратите внимание, что в приведенной выше матрице внедрения каждая строка соответствует слову, а каждый столбец соответствует измерению (оси).Обычно мы храним это в плотном формате, где у нас есть список слов и идентификаторов строк, которые сопоставляются с соответствующей строкой матрицы. В приведенном выше примере у нас был бы следующий список в дополнение к матрице:
{привет: 0, там: 1, техас: 2, мир: 3,…}
- Мы, очевидно, не можем имеют бесконечные строки в этой матрице, поэтому они обычно обрезаются, скажем, на 50 000 — это должны быть 50 000 наиболее распространенных слов. Если мы когда-либо видим слово только в одном контексте, трудно определить его значение (например,g., трудно выучить некоторые слова, которые у нас нет причин часто употреблять). Любое слово в наборе данных, которого нет в нашем списке, помечается как UNK, что означает, что мы не увидим его достаточно раз, чтобы быть полезным. UNK-слова настолько редки, что мы обычно можем их игнорировать.
- Матрицы вложения очень большие! Если у нас есть 50 000 слов и 300 измерений, это означает, что у нас есть 50 000 x 300 отдельных чисел. Если эти числа являются числами с плавающей запятой (4 байта), нам потребуется 50 000 x 300 x 4 байта — 60 МБ для одной матрицы!
Если бы мы могли сгенерировать эти 50 000 x 300 чисел, то теоретически у нас был бы «словарь» всех 50 000 слов, закодированных в числах.Это было бы очень полезно для разработки моделей машинного обучения, поскольку им больше не приходилось иметь дело с беспорядочными строками.
Как и для любой другой обучающей задачи, вам нужен какой-то набор данных для обучения встраиванию. Сложность состоит в том, что, в отличие от большинства функций затрат на глубокое обучение, у нас нет «реальных» вложений для расчета полезной потери (ошибки). Таким образом, у нас нет лучшего выхода, чем тренироваться для какой-то другой цели, которую мы можем протестировать и, надеюсь, создать вложения в качестве побочных продуктов — параметров — на этом пути.
Одна из методологий заключается в разработке модели, позволяющей угадывать контекст слова из самого слова. Это полезно, потому что позволяет нам всегда проверять, правильно ли угадала модель, в то время как проверить правильность внедрения невозможно.
Матрица внедрения инициализируется случайным образом и задается в качестве параметров этой модели определения контекста. Стоимость можно рассчитать, посмотрев, насколько точно модель угадала встраивание контекста, после чего всю модель можно обучить с помощью градиентного спуска.Это модель «непрерывного набора слов», предложенная Миколовым и др. В 2013 году.
После обучения матрицы внедрения на основе набора данных было бы неплохо изучить вложения, чтобы увидеть, имеют ли они смысл. На самом деле нет никаких гарантий, потому что в процессе обучения может пойти не так, как надо:
- Набор данных может быть недостаточно общим (возможно, вложения нескольких слов хороши, но не все 50 000).
- Возможно, набора данных недостаточно для обучения встраиваний.В этом случае любой метод обучения запомнит набор данных, создав вложения мусора.
- Мы могли выбрать неправильную размерность для наших вложений.
- Возможно, у выбранной нами модели обучения есть недостаток, заключающийся в том, что она не сходится должным образом.
- Один из наших гиперпараметров (параметры, которые являются частью модели, но не обучены моделью, которую мы задали перед процессом обучения) может привести к тому, что он не сойдется должным образом.
Таким образом, определенно необходимо оценить модель, но оценить вложения не так просто, как оценить другие задачи машинного обучения, потому что модель изучает вложения только как побочный продукт угадывания какой-то другой задачи ( например, значение слова в зависимости от контекста).Мы могли бы проверить, насколько хорошо модель угадывает контекстные слова, но само по себе это не так уж и полезно.
Можно использовать несколько других методов:
- Для встраивания данного слова мы можем проверить слова , ближайшие к этому слову. Если мы думаем о словах как о точках в пространстве, то для любых двух слов существует расстояние между ними. Если наша матрица внедрения была успешно обучена, синонимы должны появиться ближе друг к другу.
- Соотношения слов:
« King» означает « Queen» как « Man» означает X
Когда у нас есть вложения, мы можем преобразовать вышеуказанное отношение в уравнение:
King – Queen ~ Man – X
- В семантическом наборе данных, который имеет много подобных отношений, если вложения обучены правильно, X выше должно быть тем, что мы ожидаем: « Woman .”
- Наконец, существуют другие модели машинного обучения, которые предназначены для использования встраивания слов в качестве входных данных. Если наши вложения кажутся правильными, мы могли бы использовать их в качестве входных данных для другой модели, которая тренирует что-то еще, например, анализ настроений.
Возможность правильного обучения матриц внедрения является необходимым условием для большинства моделей машинного обучения НЛП, но работа с матрицами внедрения порождает некоторые инженерные проблемы. Матрицы довольно большие, и они не следуют тем же предположениям, для которых были разработаны тензорные структуры.В моделях обработки изображений параметры обычно плотные (вся матрица обучается и обновляется на каждом шаге), однако при обучении с встраиваемыми матрицами мы обычно обучаем только строки (слова), относящиеся к текущему контекстному окну в наборе обучающих данных. Подавляющее большинство матрицы не изменяется на данном этапе обучения.
В случае с одним узлом, поскольку нам все еще нужно хранить всю матрицу, это не имеет большого значения, но при распространении модели обучения это имеет серьезные последствия.Как правило, при глубоком обучении мы распределяем модели по кластеру, используя параллелизм данных, метод, при котором каждый рабочий узел в кластере работает с одной и той же моделью, но с разными данными. Затем они координируют обновления, которые будут вносить в параметры — минимальную информацию, необходимую для совместной работы. При работе с плотными параметрами такая координация просто означает, что каждый воркер копирует свои параметры друг другу. Однако разреженные матрицы, такие как матрица внедрения, можно сделать намного более эффективными, если они передают только измененные строки.Большинство параметров копировать не нужно.
Итак, как мы можем эффективно передавать определенные строки матрицы по сети? Следующие практические правила основаны на нашем исследовании:
- При копировании данных всегда эффективнее делать это массово, а не по одному. Например, если у нас есть 100 строк для передачи, лучше выполнить одну передачу со всеми объединенными, чем выполнять 100 отдельных передач. Это также верно для передачи памяти и графического процессора.
- Объединение следует выполнять на месте (без использования нового буфера), чтобы сократить накладные расходы ОЗУ.
- После объединения строк необходимо указать, откуда пришли исходные строки. Это можно сделать двумя способами: с помощью массива индексов или растрового изображения. Оптимальный способ зависит от процента строк, которые необходимо скопировать, и оба способа могут быть сжаты.
- На самом деле некоторые строки отображаются чаще, чем другие: независимо от языка, слова подчиняются zipfian-распределению, а не равномерному распределению. Это имеет значение, если вы намереваетесь разделить свое общение (разделить матрицу встраивания на несколько разделов).Например, если матрица внедрения отсортирована в порядке от наиболее часто употребляемых слов до наименее часто используемых, и мы хотим разбить эту матрицу на четыре раздела, первый раздел будет обновляться гораздо чаще, чем последний. В идеале мы должны рандомизировать строки матрицы, чтобы разделение матрицы на разделы не приводило к тому, что одни разделы обновлялись чаще, чем другие.
Проектирование систем для машинного обучения всегда связано с компромиссом. Чем мощнее фреймворк, тем сложнее его использовать.Матрица внедрения могла бы вписаться в стандартную форму тензора, как и любой другой параметр глубокого обучения, но если бы мы относились к ней как к любому другому параметру, мы бы потеряли возможность использовать преимущества ее разреженности (тот факт, что ее не нужно обновлять все вместе).
Если мы передаем только минимальную измененную информацию — строки матрицы внедрения, которые были обновлены для данного шага — мы можем распределить всю работу, передавая меньше информации. Это эффективно увеличивает эффективность распараллеливания задачи в целом.
Матрицы вложения — не единственные параметры особого случая в машинном обучении — разреженность может проявляться во многих формах. В общем, параметры можно разделить на три категории: хранятся и передаются редко (аналогично хэш-картам), хранятся плотно и редко передаются (встраиваемые матрицы) или хранятся и передаются плотно (традиционные тензоры). При разработке систем для решения больших семейств алгоритмов машинного обучения необходимо поддерживать все три семейства.
Разреженная матрица и ее представления | Набор 1 (с использованием массивов и связанных списков)
класс Узел:
__slots__ 17 " » «строка col « , " data " , " next "
def __init __ ( self 8, row16 8, row16 8, row16 8, row , столбец = 0 , данные = 0 , следующий = Нет ):
строка = строка
self .col = col
self .data 0816 = 908 916 данных 9 . следующий = следующий
класс Редкий:
def __init __ сам .головка = Нет
self .temp = Нет
self .размер
0
9 922 9 900
def __len __ ( self ):
возврат self .размер
def isempty ( self ):
возврат возврат self 0
def create_new_node ( self , строка, столбец, данные): 0
65 7 0
65 2 9000 = Узел (строка, столбец, данные, Нет )
if self .isempty ():
self .head = newNode
else :
self .817. следующий = newNode
self .temp = newNode
self. self.размер + = 1
def PrintList ( самопроизв. r = s = self .head
print ( "row_position:" , end = ") а темп! = Нет :
печать (темп.ряд, конец = "" )
темп = темп. следующий
печать ()
печать ( "column_postion:" , конец = 8168908 а р! = Нет :
печать (r.столбец, конец = "" )
r = r. следующая
печать ()
печать ( "Значение:" , конец = "16 "
908 а с ! = Нет :
печать (s.данные, конец = "" )
с = с. следующий
печать ()
if __name__ = = «__main__000» 9228 9228 s = Редкое ()
разреженное Матричное = [[ 0 , 908, 908, 3 , 4 ],
[ 0 , 0 , 5 , 7 ],
[ 0 , 0 , 908 17 0 , 0 , 0 ],
[ 0 , 2 , , , 908 0 ]]
для i дюйм диапазон ( 4 ):
8 j 908 ( 5 ):
if sparseMatric [i] [j]! = 0 :
с.create_new_node (i, j, sparseMatric [i] [j])
s.PrintList ()
NEXT-900 pro1600 908 представляет матрицу серии
NEXT-proaudio представляет серию Matrix
NEXT-proaudio сосредоточилась на установленных и небольших портативных звуковых решениях, добавив в свой каталог серию Passive Column Array.
Пассивные колоночные массивы MATRIX состоят из близко расположенных ультрасовременных 3-дюймовых неодимовых преобразователей, размещенных в стильном и в то же время прочном алюминиево-деревянном шасси, разработанном как идеальная колонная акустическая система в архитектурной интеграции, состоящая из двух моделей: MATRIX M8 ( 8x3 дюйма) и MATRIX M3 (3x3 дюйма).
Эти массивы громкоговорителей были разработаны для обеспечения максимальной разборчивости при высоком уровне звукового давления и более широкой частотной характеристике, обеспечивая при этом постоянную ширину луча в пределах выбираемого пользователем вертикального покрытия.Такое точное управление лучом распространяется на частоту до 10 кГц, что значительно превышает эталонный показатель 4 кГц для традиционных динамиков с одним драйвером. Чтобы лучше контролировать низкие частоты, инженерами NEXT-proaudio была разработана диполярная технология Tuned Dipolar, которая обеспечивает гораздо более последовательное управление низкочастотной структурой, чем другие системы аналогичного размера.
Переключатель режимов Музыка / Вокал, выбираемый пользователем, позволяет быстро и легко оптимизировать систему. Музыкальный режим обеспечивает ровную сбалансированную частотную характеристику, а вокальный режим добавляет присутствие среднего диапазона для повышения разборчивости речи.
Колонны NEXT MATRIX способны фокусировать акустическую энергию там, где это необходимо, в зоне прослушивания, что приводит к значительному улучшению разборчивости речи и четкости музыки даже в критических акустических средах.
Для еще большей универсальности диаграмму вертикальной дисперсии можно переключать на широкую или узкую зону покрытия.
Небольшие массивы обычных колонных громкоговорителей не обеспечивают значительного контроля вертикальной направленности на более низких частотах из-за своего физического размера.Чтобы лучше контролировать низкие частоты, была разработана диполярная технология настройки, обеспечивающая более последовательное управление низкочастотной диаграммой, чем другие системы аналогичного размера. Это может быть полезно для уменьшения стимуляции резонансных комнатных мод на низких частотах. Сердцем массивов столбцов NEXT MATRIX является внутренняя плата обработки. Эта запатентованная специальная схема обеспечивает оптимизацию массива и позволяет пользователю легко настраивать поведение системы в соответствии с требованиями приложения.Для архитектурной интегрированной установки 16-миллиметровая полость в задней части динамика обеспечивает достаточно места для скрытой проводки динамика, даже когда динамик установлен ровно у стены. Съемный входной винтовой разъем обеспечивает надежную, простую и эффективную проводку. Доступны различные аксессуары для соединения, подвешивания и крепления на стене или опоре. Для работы с высоким импедансом (100 В) доступен дополнительный многоотводный трансформатор.
Эта серия подходит для стационарной установки, баров, клубов и ресторанов, звукоусиления, транспортных залов, молитвенных домов, а также аудиторий с критическими средами.
Официальная презентация состоится на выставке ISE Amsterdam на стенде NEXT-proaudio.
Для получения дополнительной информации: www.next-proaudio.com/series/matrix
Дополнительная информация:
Фотогалерея
Матрица перехода
с использованием вычисленных таблиц
ОБНОВЛЕНИЕ 2020-11-11 : Вы можете найти более полных подробных и оптимизированных примеров для этого расчета в статье DAX Patterns: Transition matrix + видео о daxpatterns.com.
Рейтинг
- важная часть любого бизнеса. Вы можете ранжировать своих клиентов, продукты или любой бизнес-актив, используя какое-либо правило. В этом примере мы используем очень простой рейтинг, основанный на количестве проданных за год. Для выполнения этого действия мы используем следующую таблицу:
Категория E - наихудшая, и клиенты в категории получают рейтинг 1 (наименьшее значение), тогда как клиенты в категории A являются лучшими и оцениваются в 5. Обычно вы храните такую таблицу в SQL, но, поскольку статья посвящена вычисляемым таблицам, я предпочитаю создавать ее, используя следующий код DAX:
SaleCategory =
СОЮЗ (
ROW ("MinSales", 0, "MaxSales", 5000, "Категория", "E", "CategoryLevel", 1),
ROW ("MinSales", 5000, "MaxSales", 10000, "Категория", "D", "CategoryLevel", 2),
ROW ("MinSales", 10000, "MaxSales", 20000, "Категория", "C", "CategoryLevel", 3),
ROW ("MinSales", 20000, "MaxSales", 40000, "Категория", "B", "CategoryLevel", 4),
ROW ("MinSales", 40000, "MaxSales", 99999999999, "Категория", "A", "CategoryLevel", 5)
)
Когда таблица находится в модели, вы не можете создать отношения между ней и клиентами, потому что категория клиента меняется каждый год.Это выглядит идеальным сценарием для динамической сегментации, и на самом деле, если вас интересует только чисто динамическая сегментация, вы можете следовать этому хорошо известному шаблону.
Вместо этого вы заинтересованы в том, чтобы проверить, как категория клиентов развивается с течением времени, используя матрицу перехода для такого атрибута. Если, например, у клиента была оценка «А» в 2008 г. и «D» в 2009 г., тогда он стал худшим покупателем, и вы хотите понять, сколько ваших клиентов переходят из одной категории в другую или, учитывая группу клиентов, повышается или понижается их рейтинг в среднем.
Сценарий можно решить с помощью чистого кода DAX, создав некоторые довольно сложные меры. Например, вы можете вычислить уровень категории клиента в текущем и предыдущем году, используя эти два показателя:
Клиент [CatLevel]: =
VAR
SalesCurrentYear = [сумма продаж]
ВОЗВРАЩАТЬСЯ
РАССЧИТАТЬ (
ЦЕННОСТИ (SaleCategory [CategoryLevel]),
SaleCategory [MinSales] = SalesCurrentYear
)
Клиент [CatLevelLastYear]: =
VAR SalesLastYear =
РАССЧИТАТЬ (
[Объем продаж],
SAMEPERIODLASTYEAR ('Дата' [Дата]),
ВСЕ ('Дата')
)
ВОЗВРАЩАТЬСЯ
РАССЧИТАТЬ (
ЦЕННОСТИ (SaleCategory [CategoryLevel]),
SaleCategory [MinSales] = SalesLastYear
)
После того, как две меры установлены, вы можете просто вычислить AVERAGEX для клиента разницы между ними, чтобы вычислить среднее отклонение в категории:
AvgVariation: = AVERAGEX (Клиент, [CatLevel] - [CatLevelLastYear])
Очевидно, что вам нужно будет добавить некоторую условную логику в особом случае, когда клиент не существовал в предыдущем году, потому что в таком случае вы вычислили бы неправильный вариант.Эти меры не являются ни слишком сложными, ни медленными, но для больших наборов данных они используют много ресурсов ЦП, потому что им нужно вычислять одно и то же значение снова и снова. Более того, это решает только проблему вычисления среднего отклонения, но, если вы хотите подсчитать количество клиентов, которые перешли из одной категории в другую, тогда вам нужно засучить рукава и:
- Создайте два фиктивных измерения: одно для категории, которая была у клиента в прошлом году, а вторая для категории, которая была у клиента в этом году
- Используйте вариант шаблона динамической сегментации для вычисления количества клиентов в каждом сегменте, используя предыдущую или текущую категорию, выбранную из одного из предыдущих технических измерений
Бессмысленно предоставлять полное решение в этой статье, мы заинтересованы только в том, чтобы сказать, что решение, хотя и существует, является сложным и скорость этих вычислений не на высшем уровне.
Намного лучше создать таблицу, содержащую всю необходимую информацию в одном месте, а именно:
- Имя клиента
- Календарный год
- Категория и уровень в данном году
- Категория и уровень в предыдущем году
Такой стол имеет множество преимуществ:
- Она намного меньше таблицы фактов, ее размер будет Клиентами x Годами
- Он уже содержит, хотя и денормализован, текущую и предыдущую категории, что делает два фиктивных измерения бесполезными.
- Это делает вычисление среднего отклонения простым СРЕДНЕМ, что также дает возможность вычислить среднее значение за несколько лет
- Поскольку он содержит ключ клиента, он полагается на физические отношения для выполнения сечения по атрибутам клиента, что приводит к чистым запросам механизма хранения
Это прекрасный пример, когда вычисляемая таблица DAX идеально подходит.Вы можете написать запрос, который вычисляет такую таблицу, используя следующий код:
CustomerCategoryByTear =
ADDCOLUMNS (
СОЗДАТЬ (
СОЗДАТЬ (
ADDCOLUMNS (
ПОДВЕСТИ ИТОГИ (
Продажи,
Клиент [CustomerKey],
"Дата" [календарный год]
),
«Продажи в год», [Сумма продаж],
«Продажи вПредыдущий год», РАССЧИТАТЬ (
[Объем продаж],
SAMEPERIODLASTYEAR ('Дата' [Дата]),
ВСЕ ('Дата')
)
),
РАСЧЕТНАЯ (
ВЫБРАТЬСТОЛБЦЫ (
ПродажаКатегория,
"CategoryLevel", SaleCategory [CategoryLevel],
"Категория", SaleCategory [Категория]
),
ФИЛЬТР (
ПродажаКатегория,
А ТАКЖЕ (
SaleCategory [MinSales] <[SalesInYear],
SaleCategory [MaxSales]> = [SalesInYear]
)
)
)
),
РАСЧЕТНАЯ (
ВЫБРАТЬСТОЛБЦЫ (
ПродажаКатегория,
"CategoryLevelPreviousYear", SaleCategory [CategoryLevel],
"CategoryPreviousYear", SaleCategory [Категория]
),
ФИЛЬТР (
ПродажаКатегория,
А ТАКЖЕ (
SaleCategory [MinSales] <[SalesInPreviousYear],
SaleCategory [MaxSales]> = [SalesInPreviousYear]
)
)
)
),
"Дельта", ([CategoryLevel] - [CategoryLevelPreviousYear])
)
В этом запросе есть несколько интересных моментов:
- Используя GENERATE вместо GENERATEALL, мы неявно удаляем все строки, в которых клиент не попал в категорию за оба года.Запрос только вычисляет эффективные вариации в рейтинге, избегая особых случаев, когда клиент полностью прекращает покупать (у него нет категории в текущем году) или он является новым клиентом (у него не было категории в предыдущем году)
- Используя GENERATE и SELECTCOLUMNS, вы можете вычислить категорию и ее уровень с помощью одного поиска
- Обратите внимание, что мы избегали (это лучшая практика) использовать SUMMARIZE для вычисления Sales и SalesLastYear. Вместо этого мы использовали пару ADDCOLUMNS и SUMMARIZE, чтобы получить лучшую скорость и безопасные результаты
Мы использовали базу данных Contoso для тестирования меры.Таблица фактов содержит 12 миллионов строк, тогда как таблица, полученная в результате этого запроса, содержит только 35 тысяч строк. Как естественное следствие, запрос к этой таблице дает отличную производительность, и вы можете легко построить матрицу, подобную следующей, которая показывает, сколько клиентов принадлежит к каждой категории и году и из какой категории они происходят:
Поскольку матрица показывает только вариации , числа на первый взгляд могут показаться неверными. Например, в 2008 году в классе E было 4 029 клиентов, но только 4 028 перешли в другую категорию в 2009 году, один является полностью потерянным клиентом и не фигурирует в этом отчете).
Если вас интересует средний разброс клиентов, вы можете легко построить СРЕДНЕЕ значение Delta и отобразить его на матрице, подобной следующей (показывающей среднее изменение по стране и году) с хорошим средним изменением за все указанные годы. в столбце Всего:
Модель вполне можно улучшить, назначив отрицательное влияние на потерянных клиентов и положительное - на новых клиентов, чтобы лучше представить бизнес, но для этого требуется более точное определение показателей, и выходит за рамки чисто технической статьи.
Само собой разумеется, что с помощью Power BI вы можете проецировать ту же информацию на карту, улучшая воздействие ваших презентаций:
Есть еще много сценариев, в которых вычисляемые таблицы сияют, предел - только ваше воображение. Вычисляемые столбцы полезны для сохранения отдельных чисел, тогда как сила вычисляемых таблиц заключается в том, что они могут сохранять целые таблицы с разной степенью детализации, что значительно снижает необходимость написания кода ETL в ваших решениях.

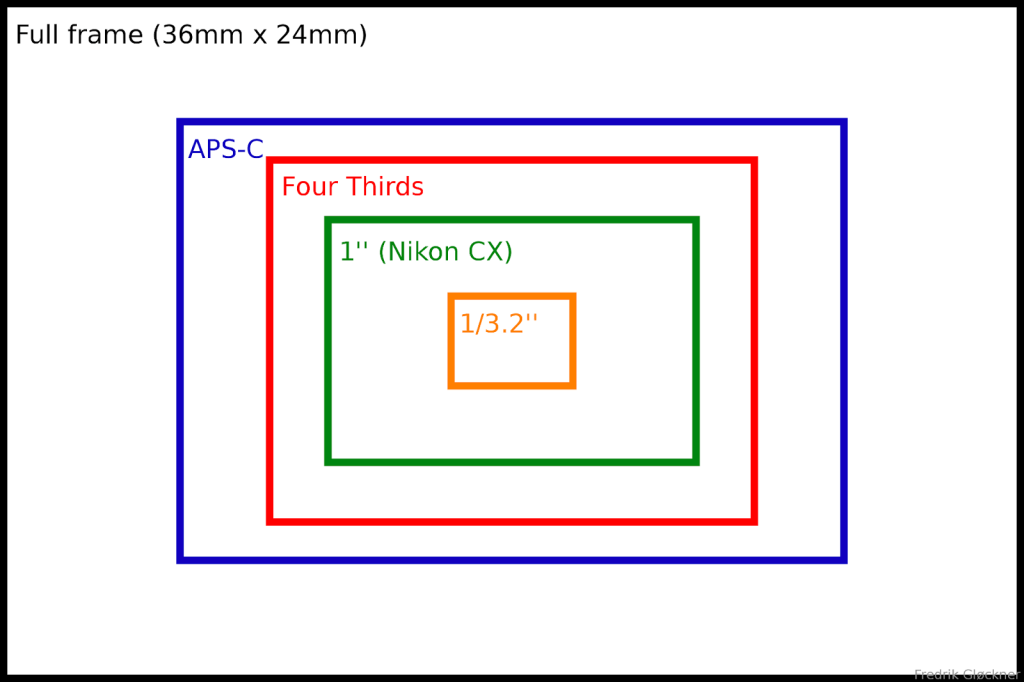 Естественно, стоить она будет много больше, чем «скромные» конкуренты, поэтому рекламировать их гораздо выгоднее.
Естественно, стоить она будет много больше, чем «скромные» конкуренты, поэтому рекламировать их гораздо выгоднее.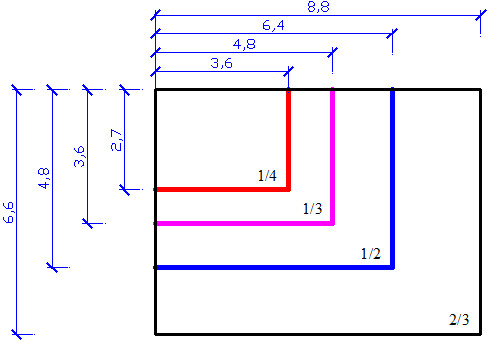 Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;
Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;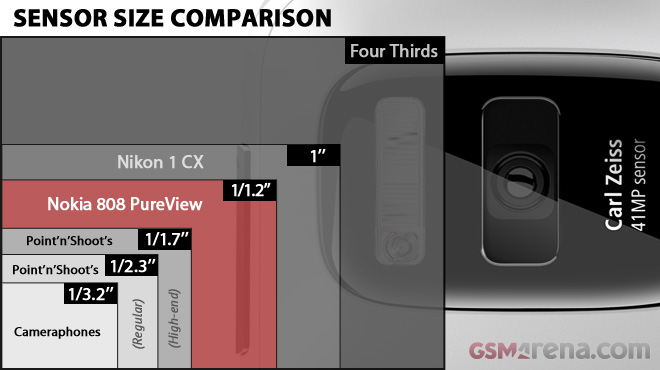 Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП.
Поскольку данная система является более современной, она зачастую оснащается автоматической подстройкой времени экспонирования каждого пикселя по отдельности. Данное улучшение позволяет получить полный кадр без потери боковых границ, а так же без потери верха и низа кадра. Полноразмерная матрица чаще всего бывает выполнена по технологии КМОП. Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).
Влажная щетка пропитана специальным раствором, который эффективно удаляет засохшие песчинки и пылинки, не оставляя пятен и разводов. Необходимо проводить по стеклу плавными аккуратными движениями, лишь слегка нажимая на саму щетку. Оставшаяся влага довольно быстро испарится сама. Даже если после влажной уборки на стекле остается пара капель, то они прекрасно удаляются сухой щеточкой (кисточкой).