учим плоские и объемные геометрические фигуры
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Зачем ребенку учить геометрические фигуры?
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений. Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
- развивать пространственное мышление, ориентацию в пространстве;
- расширять кругозор;
- развивать способность сравнивать, анализировать, обобщать и выделять главное, классифицировать;
- пополнять словарный запас.
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Как учить геометрические фигуры с дошкольником?
- Обучение для дошкольников должно строиться в виде увлекательной игры.
- Не нужно ругать ребенка, если он не запомнил названия фигур с 1 раза, даже если с 31 – не стоит.
- Не забывайте органично вплетать геометрические познания в жизнь: «подай квадратную коробочку», «возьми яблоко с круглой тарелки».

- По дороге в сад ищите предметы прямоугольной или круглой формы, соревнуйтесь, кто больше найдет и назовет.
- В игровом арсенале у вас должны быть игрушки правильной геометрической формы — мячи, кубики, детали конструктора.
- Обычно малыши любят помогать маме на кухне. Приобретите круглые, квадратные, прямоугольные формочки и испеките съедобные геометрические фигуры.
- Важно при изучении фигур задействовать и тактильную память. Ребенку гораздо интереснее будет не только увидеть, но и пощупать, погладить, а может еще и лизнуть объект изучения.
- Нагружайте мозг ребёнка дозировано, постепенно дополняя информацией. Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Основные техники и методики запоминания фигур
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
- До достижения 1,5 лет проговариваем вслух окружающие предметы, снабжая свой рассказ информацией о форме (давай возьмем круглое яблоко).

- В возрасте 1,5 — 2 лет пользуемся картинками, раскрашиваем фигуры, используем сортеры для изучения фигур. Начинаем с самого простого — круга. Остальные фигуры будем подключать только после того, как ребенок усвоил понятие «круг».
- С 2 лет до достижения школьного возраста можем применять все существующие методики, следуя от простого к сложному.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.
4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры.
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
Учим объемные геометрические фигуры
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
- Найти объемную фигуру по плоскому образцу — отличное упражнение на развитие пространственного мышления.
- «Сыщик». Детям раздают «ориентировку» – плоский рисунок искомой фигуры со всех сторон. Детям необходимо сопоставить картинки и найти нужную фигуру.

- Создать трехмерную модель самому. Взрослый может распечатать трафареты с интернета. Ребенку остается согнуть по линиям и склеить, чтобы получилась фигура.
- Макеты, оригами – можно попробовать с вместе с ребенком создать свою объемную игрушку из бумаги.
- Конструктор. Постройте при помощи деталей башню или замок для принцессы. Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.
Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Стеклянная кубическая призма.
 Колхозим интересную подсветку для фото
Колхозим интересную подсветку для фото
В своей любви к фотографии (возможно, не всегда взаимной) я уже недавно признавался. Сегодня есть повод рассказать, как можно “сделать красиво”, потратив небольшую сумму и использовав минимум подручных материалов.
Такого у меня еще не было — вчера получил заказ, сегодня уже строчу обзор. Так меня вдохновил этот малюсенький стеклянный кубик, что аж руки зачесались. Поэтому, представленная в обзоре конструкция по уровню исполнения недалеко ушла от детсадовских поделок. Это ни в коем случае не законченное изделие, а скорее макет, собранный по принципу “я его слепила из того, что было”. Но, если вы перфекционист, то лучше пропустите этот обзор.
Шел кубик долговато — с 9 марта. Упаковка — пупырчатый пакет.
Кубик небольшой — грань 1,26 см (0,5 дюйма).
Если вам покажется, что на фотографиях вы видите выщербину, вам все правильно кажется, потому что я умудрился уронить его на плиточный пол в первые полчаса после вскрытия посылки.
Кубик не простой — внутри видно Х-образное пересечение. Благодаря своей конструкции он раскладывает световой поток на разные цветовые составляющие. Если направлять свет на одну из граней под прямым углом, то он раскладывается на три потока — синий, зеленый и красно-оранжевый. Если свет попадает на ребра, то разноцветные блики получаются более разнообразными и сочетание цветов на каждом ребре получается разное.
Теперь о том, что это вообще такое. Из википедии:
Дихроидная призма — устройство, разделяющее падающий на него световой поток на несколько с различными диапазонами длин волн (цветами). Строятся из одной или более стеклянных призм с дихроидными оптическими покрытиями, которые выборочно отражают или пропускают свет в зависимости от длины волны лучей света. Таким образом, определённые поверхности в пределах призмы действуют как дихроичные фильтры.
Принцип действия
Еще фото в разных ракурсах:
Зачем эта призма понадобилась мне? Ну, во-первых, это красиво. Также, когда заказывал, смутно подозревал, что смогу ее приспособить для фотоэкспериментов. После получения почувствовал, что потенциал есть и начал придумывать, как бы призму прикрутить к фонарику. Первое, что попало под руку подходящего, была пищевая фольга. Со второго раза получилось так:
Во время первой попытки призма, выпав из фольги как раз и грохнулась на пол ванной, поскольку тестовой поверхностью был белый верх стиралки.
Вытащил белый цветочек из купленного перед тем жене весеннего букетика и попробовал подсветить получившимся агрегатом.
Дальше решил добавить в “систему” искажений и с помощью той же фольги добавил линзу диаметром 3 см.
Понимая, что вид конструкции переходит все рамки приличий, наверно, спрячу фото под спойлер.
Дополнительная информация
Тем не менее, результат вполне меня радует.
Получившиеся абстракции чем-то напоминают о камнях бесконечности:)
Из-за маленьких размеров призмы для подсветки более крупных предметов она не очень подходит. Попробовал снять автопортрет. Получилось стремненько.
В общем, штука очень интересная, и как игрушка, и с точки зрения создания эффектов для фотографии. Пожалуй, стоит купить покрупнее.
Дисперсия света. Цветовой диск Ньютона
- Участник: Ворошнин Данил Александрович
- Руководитель: Базыльникова Марина Александровна
Введение
Мы живем в мире разнообразных световых явлений – радуга, полярные сияния, голубое небо. Тем, кто не знаком с причинами их возникновения, эти световые явления кажутся необыкновенными и загадочными.
В повседневной жизни мы встречаемся со многими световыми явлениями, но обычно не задумываемся над ними – насколько они привычны для нас, а вот объяснить их часто затрудняемся. Например, чайная ложка, опущенная в стакан с водой, кажется нам надломленной или сломанной, в зависимости от того, с какой стороны мы смотрим на ложку. Мы видим окружающие нас предметы многоцветными при освещении Солнцем или яркой лампой, но с наступлением сумерек или при ослаблении света цветность предметов блекнет.
Все эти явления связаны с понятием «свет». В обыденной речи «свет» мы используем в самых разных значениях: ученье – свет, а неученье – тьма, свет мой, солнышко, скажи … В физике термин «свет» имеет гораздо более определенное значение. Опытным путем было установлено, что свет нагревает тела, на которое падает. Следовательно, он передает этим телам энергию. Мы также знаем, что одним из видов теплопередачи является излучение, следовательно, Свет – это электромагнитное излучение, воспринимаемое человеческим глазом и вызывающее зрительные ощущения. Свет обладает множественными свойствами, одним таким свойством света является – дисперсия. Мы всегда сталкиваемся с этим явлением в жизни, но не всегда замечаем этого. Но если быть внимательным, то явление дисперсии всегда нас окружает. Одно из таких явлений это обычная радуга. На первый взгляд радуга это что-то простое, на самом деле при возникновении радуги происходят сложные физические процессы. Поэтому мы выбрали тему дисперсия света для того, чтобы глубже понять физические процессы и явления, происходящие в природе. Это очень интересная тема и мы постараемся в своем проекте представить все моменты, происходящие в истории развития науки о свете и показать опыты по демонстрации дисперсии света, а так же свою экспериментальную установку, разработанную специально для наблюдения дисперсии света, которая впоследствии может быть использована на уроках физики при изучении данной темы.
Свет обладает множественными свойствами, одним таким свойством света является – дисперсия. Мы всегда сталкиваемся с этим явлением в жизни, но не всегда замечаем этого. Но если быть внимательным, то явление дисперсии всегда нас окружает. Одно из таких явлений это обычная радуга. На первый взгляд радуга это что-то простое, на самом деле при возникновении радуги происходят сложные физические процессы. Поэтому мы выбрали тему дисперсия света для того, чтобы глубже понять физические процессы и явления, происходящие в природе. Это очень интересная тема и мы постараемся в своем проекте представить все моменты, происходящие в истории развития науки о свете и показать опыты по демонстрации дисперсии света, а так же свою экспериментальную установку, разработанную специально для наблюдения дисперсии света, которая впоследствии может быть использована на уроках физики при изучении данной темы.
Цель проекта – изучение понятия «Дисперсия света» и изготовление экспериментальной установки «Цветовой диск Ньютона».
Задачи:
- Изучить историю открытия И. Ньютоном явления Дисперсия света.
- Рассмотреть спектральный состав света.
- Дать понятие о дисперсии света.
- Подготовить эксперименты по наблюдению дисперсии света.
- Рассмотреть природное явление радуга.
- Изготовить экспериментальную установку «Цветовой диск Ньютона».
I. Теоритическая часть
1.1. Открытие Исаака Ньютона
В 1665–1667 годах Исаак Ньютон – английский физик и математик занимаясь усовершенствованием телескопов, обратил внимание на то, что изображение, даваемое объективом, по краям окрашено, данное наблюдение его очень заинтересовало, и он решил разгадать природу возникновения цветных полос. В это время в Англии свирепствовала эпидемия чумы, и молодой Исаак Ньютон решил укрыться от неё в своём родном Вулсторпе. Перед отъездом в деревню он приобрёл стеклянные призмы, чтобы «произвести опыты со знаменитыми явлениями цветов». Исследуя природу цветов, Ньютон придумал и выполнил целый комплекс различных оптических экспериментов. Некоторые из них без существенных изменений в методике, используются в физических лабораториях до сих пор. Главный опыт был традиционным. Проделав небольшое отверстие в ставне окна затемнённой комнаты, Ньютон поставил на пути пучка лучей, проходивших через это отверстие, стеклянную призму. На противоположной стене он получил изображение в виде полоски чередующихся цветов (рис. 1).
Исследуя природу цветов, Ньютон придумал и выполнил целый комплекс различных оптических экспериментов. Некоторые из них без существенных изменений в методике, используются в физических лабораториях до сих пор. Главный опыт был традиционным. Проделав небольшое отверстие в ставне окна затемнённой комнаты, Ньютон поставил на пути пучка лучей, проходивших через это отверстие, стеклянную призму. На противоположной стене он получил изображение в виде полоски чередующихся цветов (рис. 1).
Рисунок 1. Эксперимент И. Ньютона
1.2. Спектральный состав света
Полученную таким образом цветную полоску солнечного света Ньютон разделил на семь цветов радуги – красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый (рис. 2).
Рисунок 2. Разложение белого пучка света на спектр
Спектр – (от латинского «spectrum» – видение) непрерывный ряд цветных полос, получается путем разложения луча белого света на составные части (рис. 3).
3).
Рисунок 3. Спектр
Если же рассматривать спектр без подобного предубеждения, то полоса спектра распадается на три главные части – красную, желто-зелёную и сине-фиолетовую. Остальные цвета занимают сравнительно узкие области между этими основными.
Все цвета спектра содержатся в самом солнечном свете, а стеклянная призма лишь разделяет их, так как различные цвета по-разному преломляются стеклом. Наиболее сильно преломляются фиолетовые лучи, слабее всего – красные.
1.3. Дисперсия света
Проходя через призму, луч солнечного света не только преломляется, но и разлагается на различные цвета.
Дисперсией называется явление разложения света на цвета при прохождении света через вещество.
Прежде чем разобраться в сути этого явления, необходимо рассмотреть преломлении световых волн. Изменение направления распространения волны при прохождении из одной среды в другую называется преломлением.
Положим на дно пустого не прозрачного стакана монету или другой небольшой предмет. Подвинем стакан так, чтобы центр монеты, край стакана и глаз находились на одной прямой. Не меняя положения головы, будем наливать в стакан воду. По мере повышения уровня воды дно стакана с монетой как бы приподнимается. Монета, которая ранее была видна лишь частично, теперь будет видна полностью. Эти явления объясняются изменением направления лучей на границе двух сред — преломлением света (рис. 4).
Рисунок 4. Преломление светового луча
Закон преломления света: падающий луч, луч преломленный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости.
где n21 – относительный показатель преломления второй среды относительно первой.
При изменении угла падения α меняется и угол преломления β, но при любом угле падения отношения синусов этих углов остается постоянным для данных двух сред.
Если луч переходит в какую-либо среду из вакуума, то
где n – абсолютный показатель преломления второй среды.
Абсолютный показатель преломления – физическая величина, равная отношению синуса угла падения луча к синусу угла преломления при переходе луча из вакуума в эту среду.
Чем больше у вещества показатель преломления, тем более оптически плотным считается это вещество. Например, рубин – среда оптически более плотная, чем лёд.
Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Это было доказано французским математиком Пьером Ферма и голландским физиком Христианом Гюйгенсом. Они доказали, что
Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред, равная отношению скоростей света в этих средах:
sinα
= n21 =
V1
sinβ
V2
Скорость света в любом веществе меньше скорости света в вакууме. Причиной уменьшения скорости света в среде является взаимодействие световой волны с атомами и молекулами вещества. Чем сильнее взаимодействие, тем больше оптическая плотность среды, и тем меньше скорость света. Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.
Причиной уменьшения скорости света в среде является взаимодействие световой волны с атомами и молекулами вещества. Чем сильнее взаимодействие, тем больше оптическая плотность среды, и тем меньше скорость света. Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.
Абсолютный показатель преломления определяется скоростью распространения света в данной среде, которая зависит от физического состояния среды, т. е. от температуры вещества его плотности. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого – меньше, чем для фиолетового.
Таким образом,
Дисперсия света – зависимость показателя преломления и скорости света от частоты световой волны.
Абсолютный показатель преломления стекла n, из которого изготовлена призма, зависит не только от свойств стекла, но и от частоты (от цвета) проходящего через него света. В опыте Ньютона при разложении в спектр пучка белого света, лучи фиолетового цвета, имеющие большую частоту, чем красные, преломились сильнее красных, поэтому на экране можно наблюдать цветную полосу – спектр (рис. 5).
В опыте Ньютона при разложении в спектр пучка белого света, лучи фиолетового цвета, имеющие большую частоту, чем красные, преломились сильнее красных, поэтому на экране можно наблюдать цветную полосу – спектр (рис. 5).
Рисунок 5. Преломление светового луча при прохождении через более оптически-плотную среду – стеклянную призму
1.4. Радуга
Дисперсией света объясняются многие явления природы, например Радуга. В результате преломления солнечных лучей в каплях воды во время дождя на небе появляется разноцветная дуга – радуга (рис. 6).
Рисунок 6. Природное явление радуга
Радуга — это оптическое явление, связанное с преломлением световых лучей на многочисленных капельках дождя.
Разноцветная дуга появляется оттого, что луч света преломляется в капельках воды, а затем, возвращаясь к наблюдателю под углом в 42 градуса, расщепляется на составные части от красного до фиолетового цвета (рис.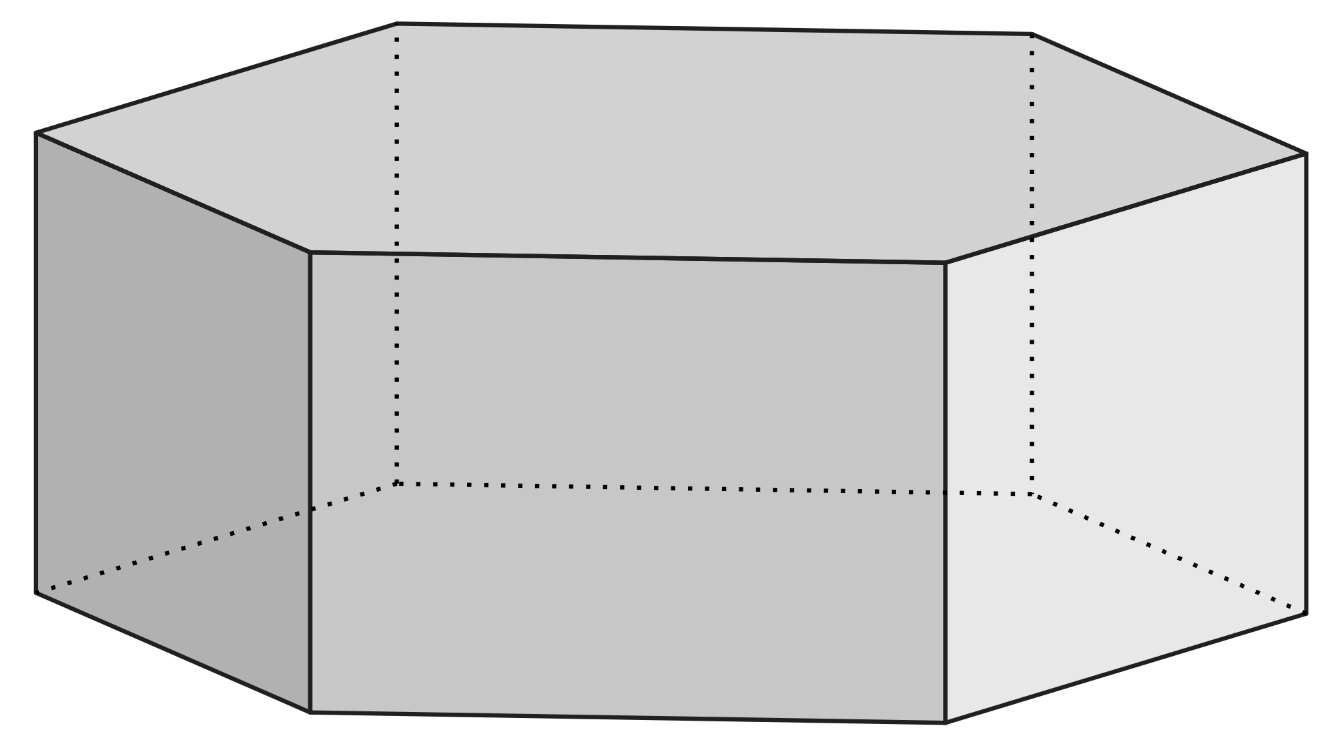 7).
7).
Рисунок 7. Преломления света в капле дождя
Прежде всего, заметим, что радуга может наблюдаться только в стороне, противоположной Солнцу. Если встать лицом к радуге, то Солнце окажется сзади. Наблюдаемые в радуге цвета чередуются в такой же последовательности, как и в спектре, получаемом при пропускании пучка солнечных лучей через призму. При этом внутренняя (обращенная к поверхности Земли) крайняя область радуги окрашена в фиолетовый цвет, а внешняя крайняя область — в красный.
Яркость оттенков и ширина радуги зависят от размера капель дождя. Чем крупнее капли, тем уже и ярче радуга, тем в ней больше красного насыщенного цвета. Если идёт мелкий дождик, то радуга получается широкая, но с блёклыми оранжевыми и жёлтыми краями.
Чаще всего видим радугу в форме дуги, но дуга – это лишь часть радуги. Радуга имеет форму окружности, но мы наблюдаем лишь половину дуги, потому что её центр находится на одной прямой с нашими глазами и Солнцем (рис. 8).
8).
Рисунок 8. Схема образования радуги относительно наблюдателя
Целиком радугу можно увидеть лишь на большой высоте, с борта самолёта или с высокой горы (рис. 9).
Рисунок 9. Радуга с борта самолета
II. Практическая часть
2.1. Демонстрация экспериментов по наблюдению дисперсии света
Изучив историю открытия дисперсии света, и процесс образования спектра, мы решили опытным путем пронаблюдать дисперсию света. Для этого подготовили и провели видео эксперименты, которые можно использовать на уроках физики при изучении темы Дисперсия света.
Эксперимент №1. Получение радужного спектра на мыльных пленках
Для проведения эксперимента понадобится: ёмкость с мыльным раствором, проволочная рамка.
Ход эксперимента: наливаем мыльный раствор в ёмкость, опускаем рамку в раствор, образуется мыльная плёнка.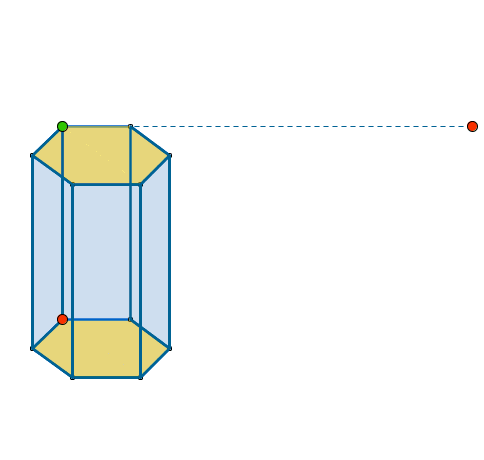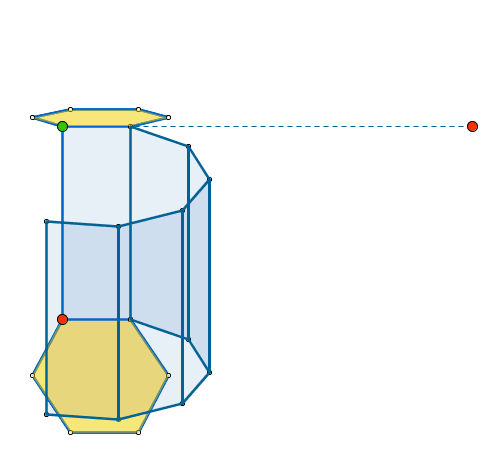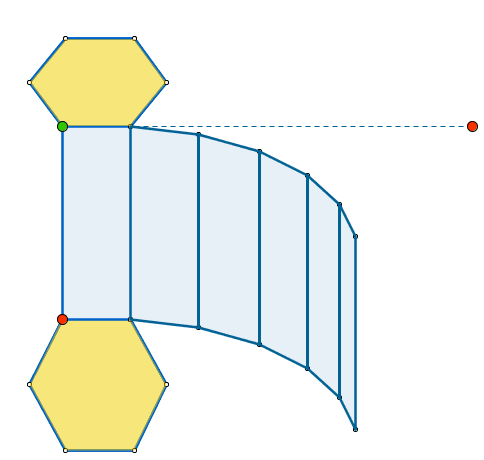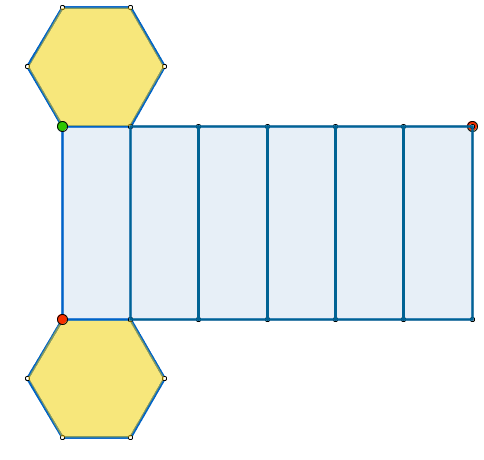 На плёнке появляется радужные полосы.
На плёнке появляется радужные полосы.
Эксперимент №2. Дисперсия света – разложение в радужный спектр пучка белого света при прохождении сквозь стеклянную призму
Для проведения эксперимента понадобится: призма, источник света (фонарик телефона), экран (лист белой бумаги).
Ход эксперимента: устанавливаем призму на экспериментальном столике. С одной стороны столика устанавливаем экран. Свет направляем на призму и на экране наблюдаем радужные полосы.
Эксперимент № 3. Дисперсия света – разложение в радужный спектр пучка белого света при прохождении через воду
Для проведения эксперимента понадобится: зеркало, источник света (фонарик телефона), экран (лист белой бумаги), ёмкость с водой.
Ход эксперимента: в ёмкость наливаем воду и кладем на дно зеркало. Направляем на зеркало свет, чтобы отраженный свет попадал на экран.
Направляем на зеркало свет, чтобы отраженный свет попадал на экран.
1.2. Цветовой диск Ньютона
Ньютон провел обычный опыт со стеклянной призмой и заметил разложение света на спектр. Направив луч дневного света на призму, он увидел на экране различные цвета радуги. После увиденного он выделил из них семь основных цветов. Это были такие цвета как: красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый (каждый охотник желает знать где сидит фазан). Ньютон выбрал лишь семь цветов по той причине, что были наиболее яркие, он также говорил, что в музыке всего семь нот, но сочетание их, различные вариации позволяют получить совершенно различные мелодии. Проведя обратный опыт, т.е. полученный спектр он направил на грань другой призмы и в результате опыта Ньютон снова получил белый свет (рис.10).
Рисунок 10. Первая призма разлагает белый свет в спектр, вторая вновь собирает спектр в белый свет
На основе этих простых опытов Ньютону пришла в голову мысль о создании круга состоящего из семи секторов и закрашенных определенными цветами в результате вращения, которого произойдет их смешение и мы получим белую раскраску этого круга. В последствии этот круг стали называть Цветной диск Ньютона (рис. 11).
В последствии этот круг стали называть Цветной диск Ньютона (рис. 11).
Рисунок 11. Цветной диск Ньютона
Попробуем повторить опыт Ньютона. Для этого создадим экспериментальную установку, которая состоит из компьютерного кулера и прикрепленного к нему цветового диска, также блока питания (рис. 12).
Рисунок 12. Экспериментальная установка по получению белого света из спектра
Кулер создает большой проток воздуха, и служит для того что бы привести во вращение цветной диск. Так как наша установка подключается в сеть с напряжением 220 В, а кулер рассчитан на 12 В, поэтому к кулеру подключили блок питания для понижения напряжения с 220 В на 12 В. Для безопасности установка изолирована в пластмассовом боксе.
В результате при включении установки в розетку сети питания цветной круг, закрепленный на кулере, начнет вращаться, и мы увидим желтовато-белую окраску круга (рис. 13).
Рисунок 13. Результат вращения цветового диск Ньютона
Окраска круга при вращении желтовато-белая по двум причинам:
- Скорость вращения круга очень низкая по сравнению со скоростью света;
- Круг окрашен с резкими цветовыми переходами, если сравнивать со спектром разложения белого света.
Таким образом, нам удалось повторить эксперименты Ньютона по разделению белого света на спектр и наоборот получение белого света из спектра.
Заключение
Окружающий нас мир играет красками: нас радует и волнует голубизна неба, зелень травы и деревьев, красное зарево заката, семицветная дуга радуги. В своем проекте мы попытались ответить на вопрос — как можно объяснить удивительное многообразие красок в природе. В целом поставленная цель об изучении такого явления как дисперсия света в итоге достигнута. Для того чтобы глубже понять такое свойство света как дисперсия, была изучена дополнительная литература по световым явлениям, были проведены эксперименты по наблюдению явления, была изготовлена установка для вращения цветового круга Ньютона с некоторой скоростью.
В результате проведенных опытов и экспериментов нами были сделаны следующие выводы:
- Дисперсия – явление разложения белого света в спектр.
- Белый цвет имеет сложную структуру, состоящий из нескольких цветов.
- При падении света на границу раздела двух прозрачных сред световые лучи различной цветности преломляются по разному (наиболее сильно-фиолетовые лучи, менее других- красные).
- Призма не изменяет цвет, а лишь разлагает его на составные части.
Таким образом, посредством теоретического изучения данной темы и ее практического подтверждения и была достигнута основная цель проекта.
Как сделать креативные фотографии с помощью хрустальной призмы для спецэффектов
Это изображение является «обычным» уличным фото. Эстакады ведут взгляд к изображению… сквозь призму
Ключевым элементом любой фотосъемки является то, как вы используете свет. В этой статье вы узнаете, как его разделить. Применение призмы при фотографировании дает новые возможности и является еще одним способом использования преломления света.
Читайте дальше, чтобы узнать о призменной фотографии, о том, как создать радугу, а также просто красивые изображения, которые выглядят как многократные экспозиции, а сделаны одним взмахом пальца!
Что призма делает со светом?
Поскольку призма является стеклянным объектом, свет преломляется при прохождении через нее, создавая несколько эффектов, которые вы можете использовать в фотографии.
Есть два способа использования призмы.
- Проецирование радуги — призма, а в частности ее треугольная форма, действуют, разделяя свет и раскрывая волны различной длины в виде радуги. А уже ее вы можете сфотографировать.
- Перенаправление света — свет может резко изменить направление при прохождении через призму. Это означает, что когда вы будете смотреть сквозь нее, сможете увидеть картину под углом 90 градусов к себе. Этот фактор дает возможность создавать двойную экспозицию.
На снимке хорошо виден радужный свет из призмы, а также остатки света, испускаемые под разными углами
Использование хрустальной призмы для создания радуги
Отличный способ использования призмы — создание радуги. Чем больше призма, тем больше в итоге получается радуга. Другой способ увеличить ее размер заключается в том, чтобы увеличить расстояние между призмой и поверхностью, на которую вы проецируете радугу. Отличие этих вариантов в том, что с увеличением вышеупомянутого расстояния радужный свет становится более рассеянным и менее интенсивным.
С помощью призмы можно создать собственную радугу
Обратите также внимание на то, как высоко в небе находится солнце. Угол падения солнечного света на призму влияет на угол проецируемой радуги. Легче спроецировать радугу на землю в полдень. Чтобы проецировать радугу горизонтальнее, необходимо фотографировать, когда солнце находится ниже в небе, то есть после восхода солнца или до его захода.
Радуга, как деталь фото
Радужный свет очень красочный, и при проецировании на поверхность это может создать интересный эффект. Ищите поверхность, которая имеет нейтральный цвет (например, серый или белый). Обратите внимание на поверхности с приятной текстурой.
Крутите призму до тех пор, пока не сможете увидеть радугу, проецируемую на поверхность, которую вы фотографируете. Можно, конечно, сделать снимок, удерживая призму и камеру. Но хорошо, если у вас есть друг, который поможет. Поскольку это детальное фото, лучше использовать макрообъектив, но можно отыскать не менее интересные композиции, используя и другие объективы.
Радуга в портретной фотографии
Несомненно, одна из самых популярных форм призменной фотографии — проецирование радуги на лицо модели. Радуга в итоге не будет большой, и было бы, снова-таки, хорошо, если бы другой человек держал призму, пока вы фотографируете.
Три изображения в одном кадре
Можно снимать через стекло те предметы, которые появляются внутри призмы. Поднимите призму и поверните ее. Вы увидите изображения внутри. При этом они не будут являться теми же, что находятся прямо перед вами. В зависимости от того, как вы повернете стеклянную призму, можно будет увидеть одно или два изображения. Именно с ними вы можете работать, чтобы создать уникальные мультиэкспозиции одним нажатием кнопки затвора.
Выбор объектива
Лучшие объективы для призменной фотографии — широкоугольные и макрообъективы.
- Широкоугольный объектив позволяет добавить фоновое изображение в фотографию. Тем не менее, край призмы становится более заметным в кадре. Нелегко размыть изображение с помощью диафрагмы, доступной на большинстве широкоугольных объективов.
- Макрообъектив. Большая часть призменной фотографии выполняется с его использованием, так как этот объектив позволяет фокусироваться близко к призме и избежать захвата руки в кадре. Переход от фона к изображению в призме также сложнее обнаружить.
Изображение снято макрообъективом с призмой, и в итоге оно выглядит как оптическая иллюзия
Диафрагма для призменной фотографии
Диафрагма, которую вы используете для таких фотографий, в основном зависит от того, что вы планируете сделать с фоном, и того, насколько четким вы хотите получить изображение в призме.
Открытая диафрагма f/2,8 или больше, безусловно, сработает для размытия заднего плана. Большинству фотографий нужен такой фон, чтобы добиться ощущения множественной экспозиции. Это означает, что апертура около f/8 является правильным балансом между фоном и деталями и позволяет избежать слишком резкой линии призмы при переходе к заднему плану.
Фоновое изображение
В силу небольшой ширины призмы даже с макрообъективом задний план занимает большую часть кадра. Так что же работает в роли фона для этого типа фотографии?
- Ведущие линии — фон, который привлекает внимание к изображениям внутри призмы используется эффективно. Это может быть туннель или дорога, уходящая в бесконечность.
- Текстурный фон — больше пустого холста для изображений в призме. Это может быть кирпичная стена или листья и цветы.
- Симметрия. Поскольку призма разделяет ваше изображение посередине, использование симметрии с обеих сторон этого разделения является довольно-таки эффективной стратегией.
Использование симметрии заднего плана может хорошо работать в призменной съемке
Изображение в стекле
Теперь самое сложное — получить хорошее изображение внутри призмы. Изображения в ней могут располагаться под углом 90 градусов к тому, как вы смотрите, или, возможно, под углом 60 градусов к краю и спереди относительно того, где стоит фотограф. Включение этого в композицию фона — сложный аспект призменной фотографии.
- Композиция — у вас уже есть хорошая композиция для вашего фона. Теперь нужно сохранить ее, одновременно добавляя точку интереса, которая бы хорошо смотрелась сквозь призму. Просто используйте метод проб и ошибок. Измените угол наклона призмы или поверните ее; можно также попробовать отойти вперед и назад.
- Добавление модели. Более простой способ добавить интерес к изображению в призме — сделать его портретной фотографией. Преимущество в том, что вы можете просто попросить модель стоять в нужном положении, из которого преломленный свет проходит через призму.
Добавление модели в композицию этого изображения сделало фотографию сакуры гораздо интереснее
Используйте фракталы
Фракталы — это еще один элемент, использующий преломление в фотографии. Они производят призменные эффекты, но сами по себе не имеют треугольной формы. Вы можете фотографировать через них, не беспокоясь о том, чтобы изображения находились под углом 90 градусов к вам. Фракталы часто используются для создания креативных портретных фотографий с мягкими краями или других абстрактных снимков.
Время идти и делить свет!
Если вы хотите попробовать что-то новое в фотографии, вам определенно понравится хрустальная призма. С ней немного сложно фотографировать, но это то, что делает процесс по-настоящему интересным. Именно сейчас пришло время взять хрустальную призму в руки и отправиться навстречу экспериментам!
Конспект НОД по конструированию в старшей разновозрастной группе. Тема: «Роботы»
Цель: упражнять в создании схем и чертежей; в моделировании и конструировании из строительного материала и деталей конструкторов; развивать воображение, внимание, сообразительность, стремление к экспериментированию, понятливость; умение строить умозаключения на основе своего опыта и здравого смысла, внимание, сосредоточенность; формировать представление об объемных телах, их форме, размере, количестве.
Материал: геометрические фигуры, фломастеры, простые карандаши, ластики, строительный материал, конструкторы, цветные карандаши (зеленый, красный, синий, желтый, оранжевый).
Ход работы
Показать детям роботов. Рассмотреть их с детьми, проанализировать строение роботов.
Есть коробка у меня,
В ней живут мои друзья.
Они очень разные,
Желтые и красные,
Зеленые и синие,
Все дружные и сильные.
Вместе любят собираться
И в постройки превращаться.
(Коробка с кубиками, конструктор.)
Педагог читает стихотворение, достает из коробки кубики поочередно, следуя тексту. (Куб, кирпичик, брусок, цилиндр, призма, конус, пластина).
Как-то кубик в лес пошел,
Там кирпичика нашел.
Взялись за руки детали,
По тропинке побежали.
А на встречу- скок-поскок-
Прибежал к друзьям брусок.
И спросил брусок:
— Детали вы цилиндра не видали!
Повернулся куб бочком:
— Я с цилиндром не знаком.
А кирпичик удивился:
— Нам на встречу он катился! (подкатить цилиндр)
Ну, пора теперь идти,
Надо призму нам найти.
Видел я ее без дела
Она с конусом сидела
У друзей пластин в гостях
С фотографией в руках.
(Показать большую фотографию и разместить ее на стенде.)
Педагог показывает картинку с роботами. Задает вопросы:
- Назовите детали из которых состоят роботы? (Куб, конус и т.д.)
- Сколько роботов изображено на картинке? (6.)
- Найдите двух одинаковых роботов и раскрасьте их оранжевым карандашом.
- Раскрасьте в красный цвет туловище тех роботов, у которых головы изображены в форме цилиндра.
- Раскрасьте в синий цвет туловище тех роботов, у которых головы изображены в форме полуцилиндра.
- Раскрасьте в зеленый цвет туловище тех, роботов у которых головы изображены в форме пирамиды.
- Раскрасьте в желтый цвет туловище тех роботов, у которого голова изображена в форме конуса.
- Сколько потребуется деталей, чтобы сконструировать желтого робота.
- Назовите эти детали.
- Покажите роботов, которых можно (нельзя) построить из данных деталей, и объясните почему.
Обратить внимание детей на робота, который сконструирован из мягких модулей для образца (две призмы, цилиндр, куб).
Предложите детям смоделировать роботов из геометрических фигур, раскладывая их на бумаге; обвести фигуры фломастерами и получить контурные схемы, затем расчленить их, конкретизировать (призма, цилиндр, куб).
Игра малой подвижности «Льдинки, ветер и мороз»
Играющие встают парами лицом друг к другу и хлопают в ладоши, приговаривая:
Холодные льдинки,
Прозрачные льдинки,
Сверкают, звенят,
Дзинь, дзинь…
Дети хлопают на каждое слово: сначала сами хлопают, затем вдвоем с товарищем. Хлопая в ладоши говорят «Дзинь, дзинь» до тех пор пока не услышат сигнал «Ветер» дети кружатся. На сигнал «Мороз» все выстраиваются в круг, и берутся за руки отводя их назад, превращая круг в большую льдинку.
Игра «Поиграем с компьютером».
Предложить детям сделать чертеж робота с аксонометрического чертежа: Рассмотреть изображение, проанализируйте его. (Можно сконструировать такого робота из конструктора.)
Задание:
- Изобразите его вид спереди в левом нижнем квадрате экрана.
- Изобразите его вид сбоку в левом верхнем квадрате.
- Изобразите его вид сверху в правом верхнем квадрате.
Предложите сконструировать роботов по своему замыслу (наборы плоских фигур).
При анализе детских работ обратить внимание на оригинальность решений и на то, какие функции могут выполнять изображенные роботы.
Для закрепления предложить детям показать сказку «Репка» с мягкими модулями.
Эльмира – репка
Даня- дед- брусок
Настя Ж- бабка- цилиндр
Настя В- внучка- призма
Вова- жучка- куб
Кристина- кошка- шар
Ксюша- мышка- призма маленькая.
Посадил брусок репку. Выросла репка большая, пребольшая. Стал брусок тянуть репку. Тянет-потянет, а вытянуть не может.
Позвал брусок цилиндра. Цилиндр за брусок, брусок за репку. Тянут потянут, а вытянуть не могут.
Позвал цилиндр призму. Призма за Цилиндр, цилиндр за брусок, брусок за репку. Тянут-потянут, а вытянуть не могут.
Позвала призма куб. куб за призму, Призма за Цилиндр, цилиндр за брусок, брусок за репку. Тянут- потянут, а вытянуть не могут.
Позвал куб шар. Шар за куб, куб за призму, Призма за Цилиндр, цилиндр за брусок, брусок за репку. Тянут-потянут, а вытянуть не могут.
Позвал шар маленькую призму. Маленькая призма за шар, Шар за куб, куб за призму, Призма за Цилиндр, цилиндр за брусок, брусок за репку. Тянут-потянут, а вытянули репку.
Конспект занятия по ФЭМП в средней группе на тему: «Призма и пирамида» | План-конспект занятия по математике (средняя группа):
Конспект занятия по ФЭМП в средней группе на тему:
«Призма и пирамида»
Цель: сформировать представление о призме и пирамиде, умение распознавать предметы в форме призмы и пирамиды в окружающей обстановке, закрепить счет до 5, представления о числе и цифре 5; закрепить знания о днях недели.
Интеграция образовательных областей: познавательное, художественно-эстетическое, социально-коммуникативное.
Материалы к занятию:
Демонстрационный: фигуры и картинки цилиндра и конуса разного размера, призмы и пирамиды, карточки с цифрами от 1 до 5, игрушка Карандашкин.
Раздаточный: фигуры призмы и пирамиды с «паспортами»; краски: красного, синего, зеленого и желтого цвета, ватные палочки, салфетки, простой карандаш. Предварительная работа с детьми: рассматривание иллюстраций о стране Египет.
Ход занятия:
Воспитатель:
Ребята, к нам пришло письмо от Карандашкина он собирается путешествовать по Египту и приглашает нас в это путешествие, но эта страна от нас очень далеко, как вы думаете, на чём быстрее можно добраться туда.
Дети: На самолёте.
Воспитатель: Ну что отправимся путешествовать?
Сначала нам нужно приобрести билеты и занять места, согласно купленным билетам (закрепление прямого счета до 5 и умение соотносить цифры 1-5 с количеством).
На самолете показывается Карандашкин:
— Здравствуйте ребята, вы письмо получили от меня?
Дети: Да.
Карандашкин: А я боялся опоздать, и прибежал прямо к самолету. Ну что, вы готовы лететь? Вперед за приключениями!
Воспитатель: Включаем свои моторы, расправляем крылья, а чтобы было веселее нам лететь, поиграем в игру «Любопытная Варвара».
Любопытная Варвара смотрит влево,
Смотрит вправо,
Смотрит вверх,
Смотрит вниз,
Чуть присела на карниз
И с него свалилась вниз.
Скатилась и забыла, как называются дни недели, давайте и мы вспомним. Воспитатель предлагает детям назвать первый, второй, пятый… дни недели.
Воспитатель: Можно приземляться. Ребята, обратите внимание, что за странные фигуры здесь в Египте? Карандашкин, расскажи нам что — это?
Карандашкин: Ребята, это знаменитая фигура Египта (показ иллюстрации) она называется «пирамида». Я знаю такой город Пирамид, там все дома такой формы. Давайте их рассмотрим, на какую фигуру они похожи?
Дети: Конус, треугольник.
Воспитатель: Ребята, присаживайтесь за столы, у вас на столе такие же фигуры, которые мы видели на картине, кто запомнил, как она называется?
Дети: Пирамида.
Воспитатель: правильно, возьмите в руки фигуры и посмотрите, с каждой стороны есть треугольные боковые поверхности, которые, на вершине постройки образуют острый угол, покажите острый угол, на какую фигуру похожи?
Дети: Треугольник.
Воспитатель: Правильно, если со всех сторон посмотреть на пирамиду мы будем видеть треугольник.
Давайте пальчиком покажем боковые грани, сколько их? Посчитаем.
Дети: Ответы детей.
Воспитатель: Молодцы.
Карандашкин: Посмотрите, ребята, я нашёл ещё одну интересную фигуру, она называется «призма». Как вы думаете, на какую фигуру она похожа?
Дети: Цилиндр.
Воспитатель: Правильно, у вас на столе есть такие фигуры?
Дети: Да.
Воспитатель: Возьмите в руки фигуру и посмотрите её боковые грани, на какую фигуру похожи?
Дети: Прямоугольник.
Воспитатель: Правильно, все боковые грани соединяются в единую поверхность, боковые грани еще можно назвать боковые ребра, проведите по ним пальчиком. Ребята, если я покачу призму, она будет быстро катиться?
Дети: Нет.
Воспитатель: А что ей мешает?
Дети: Боковые грани.
Практическая работа
Давайте поиграем в пальчиковую игру с карандашом.
Карандаш в руках катаю,
Между пальчиков верчу.
Непременно каждый пальчик
Быть послушным научу.
Дети должны отметить: красным карандашом — вершину пирамиды; синим — обвести все ребра; зеленым — обозначить вершины основания. После этого одну из граней пирамиды надо заштриховать желтым цветом.
Воспитатель: Молодцы справились.
Физкультминутка:
Раз — подняться, на носки и улыбнуться.
Два — согнуться, разогнуться,
Три — в ладоши три хлопка, головою три кивка.
На четыре — руки шире.
Пять — руками помахать.
Шесть — за парту тихо сесть.
Воспитатель: Ребята, давайте вспомним, какие фигуры вы знаете (показ фигур «конус», «цилиндр», «призма», «пирамида»), у вас на столе лежат паспорта фигур, найдите паспорт для каждой фигуры, поставьте фигуру на паспорт. А теперь соедините фигуры в группы, которые похожи друг на друга (конус — пирамида, цилиндр — призма)
Чем пирамида отличается от конуса? Призма от цилиндра? (ответы детей).
Молодцы. Ребята, а вы считать умеете?
Дети: да.
Воспитатель: А теперь поиграем в игру: «Найди фигуры».
Элина, посчитай сколько конусов? Найди цифру.
Дима, посчитай сколько пирамид? Найди цифру,
Алиса, посчитай сколько цилиндров? Найди цифру.
Максим, посчитай сколько призм? Найди цифру.
Слышится детский плач
Карандашкин: Кто здесь плачет?
Появляется мальчик и говорит, что потерялся в пустыне. А сам он из города Пирамид.
Воспитатель: Давайте, ребята, поможем мальчику, построим город из Пирамид. (Дети берут со стола фигуры призмы и ставят их в определенное место)
Карандашкин: Молодцы, пора нам возвращаться. А на чем можно ещё путешествовать.
Дети: На поезде.
Карандашкин: Правильно цепляйтесь и садитесь в свои вагоны (выстроить числовой ряд) и отправляемся в путь.
Звучит музыка
Воспитатель: Вот и приехали мы домой.
Вам понравилось наше путешествие? (ответы детей)
С кем мы путешествовали и куда?
Что мы нового узнали?
Какие фигуры?
Ещё чем мы там занимались? (ответы детей)
Деревянный конструктор Строим сами 66 деталей Краснокамская Игрушка
В Интернет-магазине «Нижегородский Почемучка» вы можете купить недорогие игрушки деревянные для всей семьи, детских садов, а также они будут отличным подарком в день рождения! Это незаменимые помощники в развитии детей разного возраста.
Игрушки деревянные очень долговечны и исправно служат не одному поколению детей, даря хорошее настроение и развивая у них важные качества и навыки.
Если вы хотите большее количество деталей, то его можно дополнить набором кубиков из дерева для детского сада, который можно найти здесь и здесь
Конструирование — один из наиболее значимых процессов в развитии ребёнка. Во время игры ребёнок знакомиться с вариантами расположения строительных форм, учиться различать и называть детали (кубик, кирпичик, призма, пластина, цилиндр) и сооружать элементарные постройки по образцу. Поддерживается желание строить самостоятельно и пользоваться дополнительными сюжетными игрушками, соразмерными масштабам построек (маленькие машинки для маленьких гаражей и т.п.).
Конструктор для конструирования в детском саду купить можно найти — ЗДЕСЬ большой выбор! (перейдите по ссылке).
Используется для развития
- мелкой моторики рук
- умения различать детали по форме, используя их названия в своей речи
- эстетического воспитания (элементов конструкторской деятельности и творчества)
- пространственных соотношений (широкий — узкий, высокий — низкий)
- анализа созданных построек
- сюжетно-ролевых игр; дорожка и дома – улица; стол, стул, диван – мебель для кукол
- восприятия, логического и пространственного образа мышления, воображения
- памяти, внимания, наблюдательности.
- Игрушка изготовлена из экологически чистых материалов: сосна, ель, берёза, липа.
- Окрашена акриловыми красками.
Деревянный конструктор Строим Сами «Цветной, 66 деталей» фабрики Краснокамская игрушка для всех детей!
Это один из самых замечательных деревянных конструкторов с огромным количеством правильных геометрических фигур.
Перед Вами — бессменный хит среди деревянных конструкторов для детских садов и заботливых родителей!
Игрушки фабрики Краснокамская игрушка купить можно как отдельно, так и в комплексе с другими деревянными конструкторами, или целыми партиями для группы в детский сад, ведь они обладают колоссальной пользой для развития ребенка!
Деревянные конструкторы для детей от Краснокамской фабрики игрушек — одни из первых игрушек Вашего малыша. В этом конструкторе для детей имеются все составляющие для начального ознакомления ребенка с азами конструирования. Детали, которых целых 66 штук, выполнены в виде основных геометрических тел и окрашены в основные цвета, а деревянные кубики послужат надежной основой для построек. Вы не только сможете конструировать различные сооружения, но и учить с детьми цвета.
С чего начать с этим деревянным конструктором от фабрики Краснокамская игрушка?
Строить можно из всего: из песка и глины, из дерева и пластика, из бумаги и картона, из дешевого «Строителя» и современного дорогого конструктора, из фольги и старых коробок от молока, из пластиковых блоков для бутылок, из ивовых прутьев, пенопласта и камешков. В общем — из всего, что вы в состоянии не только купить, но и найти.
Базовыми являются обычные геометрические тела деревянного конструктора, хорошо знакомые всем если не с раннего детства, то из школьного курса: куб, параллелепипед, призма, цилиндр и производные от них. Наборы конструктора из совершенно одинаковых деталей тоже подойдут, но как дополнительное развлечение. Стереотипные детали лишают ребенка возможности поиска неожиданных вариантов и ракурсов. Кроме того, недостаточно конструировать только по заданным образцам, даже если собрать из «лего» большую коллекцию сооружений.
Продолжение..
Строить и конструировать хорошо в детском саду, когда «пора» по возрасту, начиная с 2,5—3 лет, а иногда и раньше. Но совсем не поздно, вполне полезно и приятно моделировать и в младшей школе. А если увлечение переросло в более глубокий подростковый интерес к техническому моделированию, к конструированию в виртуальном пространстве или к экспериментальной бумажной архитектуре, то отнеситесь к этому как можно серьезнее. Кто знает?..
Конструирование и развитие
Попробуем разобраться, что происходит, когда ребенок строит башни и экспериментирует со свойствами объектов. Например, когда он пытается приладить параллелепипед на вершину призмы, а сверху пристроить цилиндр — идет процесс познания мира и одновременного становления тех психических функций, которые это познание обеспечивают. Когда ребенок сначала делает чертеж, а потом согласно своему авторскому замыслу возводит игрушечный, ненастоящий дом — он учится думать. Когда соотносит реальный и моделируемый мир, формируется его сознание.
Ребенок учится действовать и думать сообразно тем законам и правилам, которые были открыты и установлены задолго до него. Включается и обживает тот мир, в который ему предстоит узнать и который ему, по всей вероятности, придется изменять. А пока изменяется он сам.
Для обучения детей конструированию используют наборы кубиков, кирпичиков, пластин и треугольников, призм, цилиндров из строительного материала деревянного конструктора «Строим Сами 66 деталей».
Прежде всего малышей знакомят с названиями деталей, их формой, величиной, с вариантами расположения на плоскости (кирпичик лежит, стоит).
Дают представление о том, что устойчивость предмета определяется его расположением на плоскости. Необходимо показать и разъяснить детям, что форма деталей обусловливает их конструктивные свойства. Например, все стороны кубика одинаковы, поэтому он устойчив в любом положении и его можно ставить на любую грань.
Грани кирпичика различны: две боковые грани значительно больше двух других боковых граней и тем более торцевых, поэтому кирпичик, поставленный на широкую грань, более устойчив, чем кирпичик, поставленный торцом.
Устойчивость и неустойчивость различных деталей можно продемонстрировать таким образом: расставить несколько кирпичиков (от 1—7 шт.) на торцевых гранях друг за другом с интервалом, равным половине длины кирпичика, затем легонько толкнуть крайний кирпичик так, чтобы он упал на впереди стоящий, и повторять это до тех пор, пока не попадают все кирпичики.
На третьем году жизни дети учатся сооружать элементарные постройки, по-разному располагая их на плоскости: кирпичики, выложенные по горизонтали,— дорожки, поезд, трамвайная линия, забор; кубики, поставленные один на другой,— башенка, лесенка; кубики в сочетании с кирпичиками — стол, стул, диван, домик, трамвай, мост, горка.
Цель этих занятий — научить детей аккуратно соединять детали, соединяя их в стройную линию, и учитывать (но еще не называть) пространственные признаки «короткий — длинный», «узкий — широкий». (Ребенку нужно давать не менее десяти — двенадцати кирпичиков и четырех — шести пластин.)
Более сложный вид построек — мебель. Вначале каждый предмет мебели выполняется отдельно и в разных вариантах. Затем детям предлагают соорудить две-три постройки сразу (стол и стулья, стол и диван и т. п.).
Описание деревянного конструктора «Строим Сами 66 деталей от фабрики Краснокамская игрушка и их наименование:
Деревянный конструктор «Строим сами» фабрики Краснокамская игрушка включает в себя 11 видов геометрических фигур: брусок, полукуб, арка, кирпичик, цилиндры двух видов, кубики, призмы, пластины 2 видов Всего 66 деталей.
Вес: 2112 г. Размеры упаковки: 35 x 30 x 5 см
Что такое призма? — Определение, факты и пример
Prism Games
Объем твердых тел
Найдите объем твердых тел, умножив площадь основания на высоту твердого тела. Помните, что эта объемная область может быть добавлена.
охватывает Common Core Curriculum 5.MD.5.cИграть сейчасПосмотреть все игры по геометрии >>
Учитесь с полной программой обучения математике K-5
Что такое Prism
Призма — это трехмерная форма с двумя одинаковыми формами, обращенными друг к другу.Эти идентичные формы называются «основаниями».
Основание может быть треугольником, квадратом, прямоугольником или любым другим многоугольником.
Остальные грани призмы — параллелограммы или прямоугольники.
Поперечное сечение призм
Поперечное сечение геометрической формы или предмета — это форма, полученная прямым разрезом. Это также называется пересечением плоскости с трехмерным объектом.Поперечное сечение призмы, параллельное основанию призмы, такое же, как и ее основание.
Обычная и неправильная призма
Основание призмы может быть правильным или неправильным многоугольником. В зависимости от формы основания призмы бывают правильными или неправильными.
Площадь поверхности и объем призмы
Площадь поверхности призмы — это сумма площадей всех ее граней.
Объем призмы — это объем пространства внутри призмы.
Давайте посмотрим, как найти площадь поверхности и объем треугольной призмы.
Площадь поверхности = Площадь базовых треугольников + Площадь боковых параллелограммов
= 2 × (1 2 x шир x в) + 2 × (l x s) + (l x b)
= bh + 2ls + фунт
Объем = Площадь базового треугольника × длина
= (1 2 ш x в) × l
= 1 2 бхл
Пример: Рассчитайте площадь поверхности и объем следующей призмы.
Длина (l) = 12 см, высота (h) = 4 см, основание (b) = 6 см, стороны = 5 см
Площадь поверхности = bh + 2ls + lb = 6 × 4 + 2 × 12 × 5 + 12 × 6 = 24 + 120 + 72 = 216 см 2 | Объем = 1 2 мл = 1 2 × 6 × 4 × 12 = 144 см 3 |
Правая призма и наклонная призма
Когда два основания призмы идеально выровнены, а ее грани являются прямоугольниками (перпендикулярными основанию), это прямая призма, в противном случае — наклонная.Они характеризуются следующим образом:
Правая призма | Косая призма | |
| Высота | Высота по боковой кромке. | Высота — это высота за пределами призмы. |
Боковые поверхности | Боковые грани — прямоугольники. | Боковые грани — параллелограммы. |
Площадь | bh + 2ls + фунт | bh + 2ls + фунт |
| Объем | 1 2 бхл | 1 2 бхл |
Интересные факты |
Призмы с примерами
Перейти к площади или объему поверхности.
Призма — это твердый объект с:
- одинаковые концы
- плоские грани
- и тот же сечение по всей длине!
Поперечное сечение — это форма, полученная прямым разрезом объекта.
Поперечное сечение этого объекта — треугольник …
.. имеет одинаковое поперечное сечение по всей длине…
… значит, это треугольная призма .
изображения / prism-grow.js
Попробуйте нарисовать фигуру на листе бумаги А теперь представьте, что он выходит из листа бумаги … |
Никаких кривых!
Призма — это многогранник, а это значит, что все грани плоские!
Например, цилиндр не является призмой , потому что у него изогнутые стороны.
Базы
Концы призмы параллельны
, и каждый из них называется основанием.
Стороны
Боковые грани призмы — параллелограммы
(четырехсторонние формы с параллельными противоположными сторонами)
Это все призмы:
и более!
Пример: гексагональный кристалл льда.
Похоже на шестиугольник, но из-за некоторой толщины на самом деле это шестиугольная призма!
Фотография НАСА / Алексей Клятов.
Обычная и неправильная призмы
Все предыдущие примеры — это призмы Regular , потому что поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).
Вот пример неправильной призмы :
| Неправильная пятиугольная призма: | ||
| Поперечное сечение | ||
| Он «неправильный», потому что поперечное сечение не имеет «правильной» формы. | ||
Правая и наклонная призма
Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:
Площадь призмы
Площадь поверхности = 2 × Площадь основания
+ Периметр основания × Длина
Пример: какова площадь поверхности призмы с площадью основания 25 м
2 , периметром основания 24 м и длиной 12 м:
Площадь поверхности = 2 × Площадь основания + Периметр основания × Длина
= 2 × 25 м 2 + 24 м × 12 м
= 50 м 2 + 288 м 2
= 338 м 2
(Примечание: у нас есть инструмент для расчета площади)
Объем призмы
Объем призмы — это площадь одного конца, умноженная на длину призмы.
Объем = Базовая площадь × длина
Пример: каков объем призмы с площадью основания 25 м
2 и длиной 12 м:
Объем = Площадь × Длина
= 25 м 2 × 12 м
= 300 м 3
Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( наклон ), но помните, что высота находится под прямым углом к основанию:
И вот почему:
Стек может наклоняться, но имеет тот же объем
Подробнее о боковых гранях
Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)
Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!
Но если два конца не параллельны , это не призма .
639 640 863, 1826, 1827 864, 3379, 3377, 3378, 7649
Урок с призмой для детей: определение и факты — математический класс [2021]
Типы призм
Есть несколько типов призм. Держите ли вы его в руке (например, коробку для салфеток) или смотрите на фотографию, вам нужно проверить концы, чтобы увидеть, какую призму вы видите. У призмы два совершенно одинаковых конца. Основания — это термин, который мы используем для обозначения одинаковых концов призмы.Мы можем использовать форму основания призмы, чтобы назвать призму. Видите треугольник у основания? Это треугольная призма! Прямоугольник у основания означает, как вы уже догадались, прямоугольную призму. Есть квадратные призмы, пятиугольные призмы и даже шестиугольные призмы. Все зависит от формы, которую вы видите у основания!
Интересные факты о призмах
Факт №1: если бы вы могли взять нож и разрезать призму параллельно основанию, основание оставалось бы той же формы независимо от того, сколько ломтиков вы сделали — как буханка хлеба. ! Разрез призмы параллельно ее основанию называется поперечным сечением .Например, если вы разрежете прямоугольную призму прямо поперек, вы увидите прямоугольное основание на каждом срезе!
Факт № 2: Помните в описании мы говорили об использовании призмы для создания радуги на стене? Для этого возьмите призму из стекла или прозрачного пластика и поднесите ее к свету. Вы увидите отражение радуги внутри призмы! Радуга появляется потому, что форма призмы разделяет свет на отдельные цвета.Вы можете подносить его к солнечному свету и отражать радугу на разных поверхностях, например, на стене — очень круто!
Факт 3: плоские стороны призмы называются гранями . У каждой грани всегда будет четыре стороны, даже если это треугольная призма или шестиугольная призма! Если они изогнутые или у граней нет четырех сторон, это не призма.
Резюме урока
Призма представляет собой трехмерную форму с одинаковыми концами, называемыми основаниями , и плоскими сторонами, называемыми гранями .У каждого лица всегда четыре стороны. Форма основания определяет тип призмы. Если вы разрежете призму прямо вниз, параллельно основанию, вы увидите бесконечные срезы, похожие на основания. Эти идентичные срезы призмы называются сечениями . Прозрачные призмы могут отражать свет особым образом — разделяя все цвета и создавая радугу!
3d геометрических фигур — сети
Добро пожаловать в Math Salamanders Nets для трехмерных геометрических фигур для призм и пирамид.
Здесь вы найдете широкий спектр бесплатных сеток для печати различных трехмерных фигур для демонстрации или поддержки обучения математике.
У Math Salamanders есть большой банк бесплатных картинок для печати.
Каждый из листов фигур для печати доступен в цветном или черно-белом цвете.
Использование этого графического рисунка поможет вашему ребенку научиться распознавать формы и учиться
о различных свойствах фигур.
На листах с разными формами мы показали формы разных размеров и ориентации, чтобы
Ваш ребенок будет распознавать вариации одной и той же формы и замечать свойства, которые имеют все одинаковые формы.
Листы можно использовать как часть математического дисплея, как карточки или как раскраски для печати.
Здесь вы найдете наш ассортимент бесплатных сетей для призм и пирамид.
Следующие распечатки содержат сети общих трехмерных фигур, которые должен знать ваш ребенок.Каждый сетчатый лист доступен как с язычками, так и без них, чтобы облегчить склеивание.
Использование этих листов поможет вашему ребенку:
- знать свойства различных трехмерных фигур;
- распознавать различные двухмерные формы внутри трехмерных фигур;
- построить 3д фигуру из сетки;
Сети включают:
- Куб
- Кубоид (или прямоугольная призма)
- Треугольная призма
- Шестиугольная призма
- Тетраэдр (пирамида с треугольным основанием)
- Квадратная пирамида
- Гексагональная пирамида
Здесь вы найдете наш дополнительный ассортимент бумажных сетей для загрузки.
Следующие печатные формы содержат сети из ряда многогранников и других трехмерных объектов.
Каждый сетчатый лист доступен как с язычками, так и без них, чтобы облегчить склеивание.
На этой странице вы найдете информацию и рабочие листы о сетях.
Рабочие листы состоят из идентификации и сопоставления цепи, которая соответствует правильной трехмерной форме.
Здесь вы найдете наш ассортимент печатных 3D-форм,
включая сферы, конусы, кубы, пирамиды и призмы.
Следующие ниже печатные формы с трехмерными геометрическими фигурами содержат изображения общих трехмерных фигур, которые должен знать ваш ребенок.
Каждый лист доступен как в цветном, так и в черно-белом варианте.
(если хотите использовать как раскраску).
Использование этих листов поможет вашему ребенку:
- распознавать различные 3D-формы и определять грани, ребра и вершины;
- распознавать различные двухмерные формы внутри трехмерных фигур;
- распознавать 3D-фигуры в разных ориентациях и размерах.
Если вы ищете рабочие листы с трехмерными фигурами, то вы нашли нужное место.
Все наши рабочие листы с трехмерными фигурами для печати с веб-сайта размещены на веб-странице ниже.
У нас есть широкий выбор листов трехмерной формы для различных классов и возможностей.
Простыни подходят с детского возраста от детского сада и старше.
На уровне детского сада основное внимание уделяется распознаванию трехмерных и двухмерных фигур.
В 1-м классе мы начинаем определять определенные типы трехмерных фигур, такие как конусы или призмы.
Во 2-м классе мы начинаем называть формы и считать некоторые из их лиц.
В 3-м классе основное внимание уделяется определению таких свойств, как грани, ребра и вершины. Мы также начинаем расследование
связи между трехмерными фигурами и их сетями.
Саламандры-математики надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Geometry Nets — прямоугольная призма
Прямоугольник — это трехмерная фигура с шестью
прямоугольная форма
стороны. Все его углы прямые. Его также можно назвать
кубовидный.
Куб и квадратная призма — особые типы
прямоугольная призма. Имейте в виду, что квадрат — это просто особый вид
прямоугольник!
- Кубики представляют собой прямоугольные призмы, в которых все три
размеры (длина, ширина и высота) имеют одинаковые размеры. - Квадратные призмы — это прямоугольные призмы, в которых любые две
трех измерений имеют одинаковые размеры.
Коробки — это пример прямоугольных призм в реальной жизни.
Исследуйте прямоугольную призму, вырезав сетку геометрии куба,
складываем и приклеиваем язычки.
Прямоугольная призма, в которой каждое измерение представляет собой другое измерение
(все
формы — прямоугольники … без квадратов)
Прямоугольная призма — плоская:
Вы можете нарисовать это на декоративной бумаге или украсить по своему усмотрению
Прямоугольная призма — милые лица:
(цвет)
или (Ч / Б)
Праздничные прямоугольные призмы:
Прямоугольная призма — Рождество: (цвет)
или (Ч / Б)
Прямоугольная призма — День святого Валентина: (цвет)
или (Ч / Б)
Прямоугольная призма, у которой два измерения совпадают
измерение
(также известное как квадратная призма)
Квадратная призма — обычная:
Вы можете нарисовать это на декоративной бумаге или украсить по своему усмотрению
Square Prism — милые лица:
(цвет)
или (Ч / Б)
Призмы Holiday Square:
Квадратная призма — Рождество:
(цвет)
или (Ч / Б)
Квадратная призма — День святого Валентина: (цвет)
или (Ч / Б)
Прямоугольная призма, у которой все три измерения одинаковы
измерение
(также известное как
куб)
Куб — Обычный: вы можете нарисовать его на декоративной бумаге или украсить по своему усмотрению
Cube — милые лица:
(цвет)
или (Ч / Б)
Праздничных кубиков:
Куб — Рождество: (цвет)
или (Ч / Б)
Куб — День святого Валентина: (цвет)
или (Ч / Б)
Характеристики прямоугольной призмы:
- тип призмы (трехмерная форма, в которой
поперечное сечение указывает тип призмы — значит треугольная призма
имела бы треугольное поперечное сечение, прямоугольная призма имела бы
прямоугольное сечение, квадратная призма будет иметь квадрат
поперечное сечение и так далее).«Поперечное сечение» — это просто причудливый способ
говоря, что вы нарезаете предмет, как если бы вы делали буханку хлеба — каждый
«кусочек» призмы одинаков. - противоположных сторон
параллелограммы (формы напротив друг друга идентичны) - 6 граней
- 8 Вершин
- 12 кромок
Формулы прямоугольной призмы:
Площадь прямоугольной
призма =
2 (ширина x длина) + 2 (ширина x высота) + 2 (длина x высота)
Объем прямоугольной призмы
= длина x ширина x высота
Определение призмы
для детей Определение призмы
для детей
Детское определение призмы
Когда волна переходит от одной прозрачной среды к другой прозрачной … Однако есть некоторые вещи, которые люди неправильно понимают в них! 2.Твердая фигура, основания или концы которой имеют одинаковый размер и форму, параллельны друг другу, а каждая сторона представляет собой параллелограмм. Это дисперсия, которая разбивает свет на полосы разных цветов, называемые спектром. Young4us 2 Pack 6-дюймовая треугольная призма из хрустального оптического стекла для фотографии, детей, науки, обучения световому спектру, физике и фотосъемке (Набор… увидеть больше. Увеличить — значит сделать что-то больше. Пора прояснить некоторые моменты) мифы о побочных эффектах призматических очков.Призма — это особый кусок стекла, хрусталя или пластика, излучающий свет. п. 1. Использование обоих глаз делает далекие объекты более реалистичными. Учить больше. Люди используют только один глаз, чтобы смотреть в телескоп, но они используют оба глаза, чтобы смотреть в бинокль. На этой неделе мы сосредоточимся на радужной науке для детей, исследуя призмы. Определение призмы, прозрачное твердое тело, часто имеющее треугольные основания, используемое для рассеивания света в спектре или для отражения лучей света. Детям будут предоставлены красочные пластиковые модели трехмерных фигур, которые помогут им попрактиковаться в подсчете количества граней, ребер и вершин.SplashLearn — это отмеченная наградами программа обучения математике, которую используют более 40 миллионов детей для увлекательной математической практики. Очки с призмой чрезвычайно полезны для людей, которым нужно то, чего не могут обеспечить обычные очки. Значение призмы: 1. Прозрачный стеклянный или пластиковый объект, разделяющий белый свет, проходящий через него, на…. Также узнайте факты, чтобы легко понять математический глоссарий с забавной математической таблицей на сайте SplashLearn. Они научатся описывать свои свойства, например, количество граней, ребер и вершин.Преломление — это изменение направления волны, вызванное изменением скорости волны. Примеры волн включают звуковые волны и световые волны. Отражение чаще всего наблюдается, когда волна переходит из одной прозрачной среды в другую прозрачную среду. Определение призмы для детей Определение призмы Следующие тексты являются собственностью их авторов, и мы благодарим их за предоставленную нам возможность бесплатно поделиться с учениками, учителями и пользователями Интернета их тексты, которые будут использоваться только в иллюстративных образовательных и научных целях Только.Бинокли, как и телескопы, увеличивают далекие объекты, чтобы их было легче увидеть. Определение призмы, написанное для изучающих английский язык из словаря для учащихся Merriam-Webster, со звуковым произношением, примерами использования и метками для подсчета / не подсчета существительных. призма синонимы, произношение призмы, перевод призмы, определение слова «призма» на английский язык. Детей 2-х классов научат называть и определять призмы и пирамиды в процессе обучения трехмерным формам. Различные типы среды включают воздух и воду.. Призмы и пирамиды в начальной школе. Определение гексагональной призмы объяснено на реальных иллюстрированных примерах. Призмы могут предоставить детям такой забавный практический способ наблюдать и строить гипотезы о свете. Определите призму. Иллюстрированное определение прямоугольной призмы: твердый (трехмерный) объект, имеющий шесть прямоугольных граней. Вот несколько забавных способов использования призм с дошкольниками, детскими садами и учениками начальных классов. * Эта научная деятельность соответствует научному стандарту следующего поколения (NGSS) 1-PS4-3.Свет изгибается (или преломляется), потому что он движется в стекле, кристалле или пластике медленнее, чем в воздухе. Если разные цвета света движутся с разной скоростью, каждый цвет изгибается по-разному.
7 забавных образов, которые можно получить с призмой
У кого новая призма ?!
Я знаю многих из вас, так как я получил много вопросов о том, как использовать призму!
Я купил свою призму на одном Amazon, и она выглядит так (по крайней мере, так было до того, как ее уронил один из моих детей):
Я хотел бы поделиться здесь некоторыми советами, чтобы все могли их увидеть, потому что это такой забавный и недорогой инструмент, чтобы добавить творческой изюминки в вашу фотографию.
1. Светлая воздушность
Добавление яркости к изображению, вероятно, самый частый способ использования моей призмы. Солнце было позади нее, поэтому я работал здесь с отличной подсветкой. Призма держалась параллельно моей линзе вверху.
2. Двоение в глазах
Я люблю отражения и то, что их можно получить с помощью призмы! Здесь я держал призму параллельно линзе прямо посередине и поворачивал ее, пока не увидел ее отражение (солнце было у меня за спиной).Чтобы получить отражения, нужно медленно поворачивать призму и набраться терпения. Если вы будете осторожны, вы можете даже получить два отражения.
3. Радуга
Радуга — большой фаворит с призмой как для меня, так и для моих детей. Это один из самых простых способов заинтересовать их фотографиями — показать им одну из них. Лучше всего получить радугу при ярком свете и удерживании призмы параллельно линзе. При всем этом призма находилась в правом нижнем углу моего объектива и держалась под небольшим углом.
4. Радужное пламя
Извините, но я действительно не знала, как это назвать, лол. Удерживая призму параллельно линзе так, чтобы она была едва видна, вы можете повернуть призму под нужным углом и получить то, что почти похоже на пламя радуги.
5. Текстура
Удерживая призму перпендикулярно моему объективу, я смог получить небольшое размытие от призмы и этой дополнительной текстуры (иногда не чистить вещи окупается).
6. Катящийся туман
Я буду честен здесь, я не уверен, как я это получил, и я еще не смог его воссоздать, но это было слишком весело, чтобы не включать
🙂
Несколько советов по использованию призмы:
- Для использования не обязательно быть очень солнечным. Хотя вам действительно нужен свет, я использовал свой, когда солнце пряталось за облаками, и все же получил с его помощью забавные снимки.
- Призма не должна находиться между линзой и источником света.Свет отражается повсюду, поэтому, даже если вы повернетесь спиной к солнцу, вы все равно сможете преломить свет.
- Немного имеет большое значение. Эффект призмы распространяется по вашему кадру сильнее, чем вы ожидаете. Обычно достаточно разместить призму по краям линзы.